leetcode树总结

最新推荐文章于 2020-12-20 09:40:54 发布
最新推荐文章于 2020-12-20 09:40:54 发布
阅读量419 收藏 2
点赞数 1
CC 4.0 BY-SA版权
分类专栏： leetcode 文章标签： leetcode 树 二叉树 二叉搜索树 遍历
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/wonner_/article/details/103575512
本文深入探讨了二叉树与二叉搜索树的遍历、构造、序列化、路径问题及公共祖先问题，提供了递归与迭代方法，并讲解了平衡二叉搜索树的构建。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

面试中对树的考察多为二叉树、二叉查找树等。常见的二叉树操作有：

  • 前序遍历、中序遍历、后续遍历（递归、迭代）
  • 层序遍历
  • 树的高度
  • 树的路径
  • 二叉搜索树

二叉树遍历

94.二叉树的中序遍历

中序遍历定义：先左子树，后根节点，再右子树。首先给出简单的递归解法。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        inorder(root,ret);
        return ret;

    }
    public void inorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return ;
        }
        inorder(root.left,list);
        list.add(root.val);
        inorder(root.right,list);
    }
    
}

迭代解法使用栈，因为其序为左中右，所以将左子树一直压栈直到为空，开始出栈，出栈的即为根节点，加入解中，同时开始遍历右子树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (curr != null || !stack.empty()) {
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            curr = stack.pop();
            ret.add(curr.val);
            curr = curr.right;
        }
        return ret;
    }
}

144.二叉树的前序遍历

前序遍历定义：先根节点，后左子树，再右子树。递归解法与上一方法类似，只是改换了递归和加入结果集的顺序。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        preorder(root,ret);
        return ret;
    }
    public void preorder(TreeNode root, List<Integer> list) {
        if (root == null){
            return;
        }
        list.add(root.val);
        preorder(root.left,list);
        preorder(root.right,list);
    }
}

迭代解法仍然使用栈，相较中序遍历的解法，只需改换加入结果集的位置。由于是先序遍历，遍历到那个节点便将其加入结果集，将左子树持续压栈直到为空，出栈，遍历出栈节点的右子树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while ( curr != null || !stack.empty() ) {
            while (curr != null) {
                ret.add(curr.val);
                stack.push(curr);
                curr = curr.left;
            }
            curr = stack.pop();
            curr = curr.right;
        }
        return ret;
    }
}

145.二叉树的后序遍历

后序遍历递归定义：先左子树，后右子树，再根节点。递归解法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        postorder(root,ret);
        return ret;

    }
    public void postorder(TreeNode root,List<Integer> list) {
        if (root == null) {
            return;
        }
        postorder(root.left,list);
        postorder(root.right,list);
        list.add(root.val);
    }
}

迭代解法的难点在于，由于后序遍历是左右根的顺序，当从栈里拿出根节点时需判断此时其右子树是否已经遍历完成。在这里我们使用一个标记，当一棵子树遍历完成时，记录下他的根节点，作为根节点右子树遍历完成的依据。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
       List<Integer> ret = new ArrayList<>();
       Stack<TreeNode> stack = new Stack<>();
       TreeNode curr = root;
       TreeNode r = null; //记录遍历过的右子树
       while(curr != null || !stack.empty()) {
            while (curr != null) {
               stack.push(curr);
               curr = curr.left;
            }
            curr = stack.peek();
            // 判断右子树是否遍历完成
            if (curr.right == null || curr.right == r) {
                ret.add(curr.val);
                r = curr;
                curr = null;
                stack.pop();
            } else {
                curr = curr.right;
            }
       }
       return ret;
    }
}

总的来说，以上三种遍历都可用一样的递归或迭代框架实现。递归只需改变加入结果集的位置；迭代首先都将全部左子树压入栈中，在出栈时，根据不同的遍历选择不同的操作。

102.二叉树的层次遍历

给定一个二叉树，返回其按层次遍历的节点值。 （即逐层地，从左到右访问所有节点）。
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

二叉树层次遍历使用队列，由于要将每一层放在一个列表中，使用栈的长度截取队列中属于一层的节点。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if(root == null) {
            return ret;
        }
        queue.offer(root);
        while(!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            while(size>0) {
                TreeNode curr = queue.poll();
                list.add(curr.val);
                if(curr.left!=null) {
                    queue.offer(curr.left);
                }
                if(curr.right!=null) {
                    queue.offer(curr.right);
                }
                size--;
            }
            ret.add(list);
        }
        return ret;
    }
}

105.从前序遍历与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

递归构造。前序遍历第一个值即为当前树的根节点，在中序遍历中找到该根节点，左边为左子树，右边为右子树，递归构造，此时，前序遍历数组的分割由中序遍历确定的左右子树大小来分割。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return dfs(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
    }

    public TreeNode dfs(int[] preorder,int prel,int prer,int[] inorder,int inl,int inr) {
        if(prel > prer) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[prel]);
        int index = 0;
        for(int i=inl;i<=inr;i++) {
            if(inorder[i] == preorder[prel]) {  //从中序遍历找分割点
                index = i;
                break;
            }
        }
        //根据中序遍历分割点计算前序遍历分割点
        root.left = dfs(preorder,prel+1,prel+index-inl,inorder,inl,index-1); 
        root.right = dfs(preorder,prel+index-inl+1,prer,inorder,index+1,inr);
        return root;
    }
}

106.从后序遍历与中序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

与上一题一样可以递归构造，此时，后序遍历第一个值变为树的根，仍在inorder中搜索该根的位置，分为左右两子树递归构造。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return dfs(inorder,0,inorder.length-1,postorder,0,postorder.length-1);
    }

    public TreeNode dfs(int[] inorder,int inleft,int inright,int[] postorder,int postleft,int postright) {
        if (inleft > inright) {
            return null;
        }
        TreeNode root = new TreeNode(postorder[postright]);
        int index = 0;
        for(int i=inleft;i<=inright;i++) {
            if(inorder[i] == postorder[postright]) {
                index = i;
                break;
            }
        }
        root.left = dfs(inorder,inleft,index-1,postorder,postleft,postleft+index-inleft-1);
        root.right = dfs(inorder,index+1,inright,postorder,postleft+index-inleft,postright-1);
        return root;
    }
}

297.二叉树的序列化与反序列化

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

你可以将以下二叉树：

    1
   / \
  2   3
     / \
    4   5

序列化为 "[1,2,3,null,null,4,5]"

可使用二叉树层序遍历的结果作为序列化的内容，若某子树为null用“#”代表。层序遍历使用队列，同样，在通过序列内容构建二叉树时也使用队列。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        StringBuilder sb = new StringBuilder();
        Queue<TreeNode> queue = new LinkedList<>();
        if(root != null) {
            sb.append(root.val);
            sb.append(",");
            queue.offer(root);
        } else {
            return null;
        }
        while(!queue.isEmpty()) {
            TreeNode p = queue.poll();
            if(p.left == null) {
                sb.append("#,");
            } else {
                sb.append(p.left.val);
                sb.append(",");
                queue.offer(p.left);
            }
            if(p.right == null) {
                sb.append("#,");
            } else {
                sb.append(p.right.val);
                sb.append(",");
                queue.offer(p.right);
            }
        }
        return sb.toString();
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        if (data == null) {
            return null;
        }
        String[] arr = data.split(",");
        Queue<TreeNode> queue = new LinkedList<>();
        TreeNode root = new TreeNode(Integer.valueOf(arr[0]));
        queue.offer(root);
        int index = 1;
        while(!queue.isEmpty()) {
            TreeNode curr = queue.poll();
            if(arr[index++].equals("#")) {
                curr.left = null;
            } else {
                curr.left = new TreeNode(Integer.valueOf(arr[index-1]));
                queue.offer(curr.left);
            }
            if(arr[index++].equals("#")) {
                curr.right = null;
            } else {
                curr.right = new TreeNode(Integer.valueOf(arr[index-1]));
                queue.offer(curr.right);
            }
        }
        return root;
    }
}

111.二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

给定二叉树 [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回它的最小深度  2.

层序遍历，返回第一个左右子树都为null的节点深度。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        if(root == null) {
            return 0;
        }
        int level = 0;
        queue.offer(root);
        while(!queue.isEmpty()) {
            int size = queue.size();
            level++;
            while(size>0) {
                TreeNode curr = queue.poll();
                if(curr.left == null && curr.right == null) {
                    return level;
                }
                if(curr.left != null) {
                    queue.offer(curr.left);
                }
                if(curr.right != null) {
                    queue.offer(curr.right);
                }
                size--;
            }
        }
        return level;
    }
}

104.二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7
返回它的最大深度 3 。

递归，返回左右子树最大高度加一。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left),maxDepth(root.right)) + 1;
    }
}

二叉树路径问题

687.最长同值路径

给定一个二叉树，找到最长的路径，这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。

注意：两个节点之间的路径长度由它们之间的边数表示。

输入:

              5
             / \
            4   5
           / \   \
          1   1   5
输出:

2

输入:

              1
             / \
            4   5
           / \   \
          4   4   5
输出:

2

二叉树问题多可以使用递归的方法解决。用递归函数返回以递归的根节点所在的最长路径。用全局变量保存最大值。对根结节点，递归遍历左子树和右子树，若根节点的值和左子树值相等，即可在左子树递归返回值上加1作为当前值，因为路径上可以加上根节点，长度加一。递归函数返回值为根节点通过左子树、右子树中路径的较大值。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int ret = 0;
    public int longestUnivaluePath(TreeNode root) {
        dfs(root);
        return ret;
    }

    public int dfs(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int left = dfs(root.left);
        int right = dfs(root.right);
        int ansleft = 0,ansright = 0;
        if (root.left != null && root.left.val == root.val) {
            ansleft = left + 1;
        }
        if (root.right != null && root.right.val == root.val){
            ansright = right + 1;
        }
        ret = Math.max(ret,ansleft+ansright);
        return Math.max(ansleft,ansright);
    }
}

124.二叉树中的最大路径和

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

输入: [1,2,3]

       1
      / \
     2   3

输出: 6

输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42

这道题的思路与上题差不多，使用递归函数返回经过参数节点的最大路径和。递归计算左子树和右子树的最大路径和。若子树的最大路径和是大于0的，那么子树对经过根的最大路径和是有增益的，把他加到参数节点的值中，与全局最大值比较。递归函数的返回值为，参数节点值，参数节点值+左子树递归值，参数节点值+右子树递归值中的最大值。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int ret = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        dfs(root);
        return ret;
    }

    public int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = dfs(root.left);
        int right = dfs(root.right);
        int cur = root.val;
        if(left>0) {
            cur+=left;
        }
        if(right>0) {
            cur+=right;
        }
        ret = Math.max(ret,cur);
        return Math.max(root.val,Math.max(left+root.val,right+root.val));
    }
}

面试题34.二叉树中和为某一值的路径

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
给定如下二叉树，以及目标和 sum = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1
返回:

[
   [5,4,11,2],
   [5,8,4,5]
]

枚举处满足条件的路径可以使用回溯算法。定义满足加入结果集的条件，当前节点为叶节点且值为sum。否则若当前节点有左子树，加入当前节点，回溯左子树，去除当前节点。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<List<Integer>> ret = new ArrayList<>();
        if (root!=null) {
            backtrack(ret,new ArrayList<>(),root,sum);
        }
        return ret;
    }

    public void backtrack(List<List<Integer>> ret,List<Integer> curr,TreeNode root,int sum) {
        //定义满足条件
        if(root.left == null && root.right == null && sum==root.val) {
            curr.add(root.val);
            ret.add(new ArrayList<>(curr));
            curr.remove(curr.size()-1);
        }
        if (root.left!=null){
            curr.add(root.val);//加入当前
            backtrack(ret,curr,root.left,sum-root.val);//回溯
            curr.remove(curr.size()-1);//去掉当前
        }
        if (root.right!=null){
            curr.add(root.val);
            backtrack(ret,curr,root.right,sum-root.val);
            curr.remove(curr.size()-1);
        }
    }
}

二叉搜索树问题

98.验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

输入:
    2
   / \
  1   3
输出: true

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。根节点的值为 5 ，但是其右子节点值为 4 。

利用二叉搜索树的性质，中序遍历为一个递增序列。使用迭代方法中序遍历二叉树，不满足递增条件则返回false。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        double pre = - Double.MAX_VALUE;
        TreeNode curr = root;
        while(curr!=null || !stack.empty()) {
            while(curr!=null) {
                stack.push(curr);
                curr = curr.left;
            }
            curr = stack.pop();
            if(curr.val <= pre) {
                return false;
            }
            pre = curr.val;
            curr = curr.right;
        }
        return true;
    }
}

96.不同的二叉搜索树

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

动态规划。定义数组dp，dp[i]代表以1..i为节点组成的二叉搜索树有多少。1..n为节点，选择其中一个节点j作为根节点，可以构成二叉搜索树的个数是由0..j-1构成的左子树的个数乘以j+1..n构成的右子树的个数。构成二叉搜索树的个数与树中的值无关只与节点个数有关，所以可以自底向上的计算。

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i=2;i<=n;i++) {
            for(int j=0;j<i;j++) {
                dp[i] += (dp[j] * dp[i-j-1]);
            }
        }
        return dp[n];
    }
}

95.不同的二叉搜索树2

给定一个整数 n，生成所有由 1 ... n 为节点所组成的二叉搜索树。

输入: 3
输出:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
解释:
以上的输出对应以下 5 种不同结构的二叉搜索树：

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

返回所有二叉搜索树，使用递归。1..n为节点，选择其中一个节点j作为根节点，递归计算1..j-1构成的二叉搜索树和j+1..n构成的二叉搜索树进行组合。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<TreeNode> generateTrees(int n) {
        if(n==0) {
            return new ArrayList<>();
        }
        return dfs(1,n+1);
    }

    //前闭后开
    public List<TreeNode> dfs(int start,int end) {
        if(start==end) {
            return null;
        }
        List<TreeNode> ret = new ArrayList<>();
        for(int i=start;i<end;i++) {  //根节点
            List<TreeNode> left = dfs(start,i);  //左子树
            List<TreeNode> right = dfs(i+1,end); //右子树
            if(left!=null && right!=null) {
                for(TreeNode leftnode:left) {
                    for(TreeNode rightnode:right) {
                        TreeNode root = new TreeNode(i);
                        root.left = leftnode;
                        root.right = rightnode;
                        ret.add(root);
                    }
                }
            } else if (left!=null) {
                for(TreeNode leftnode:left) {
                    TreeNode root = new TreeNode(i);
                    root.left = leftnode;
                    root.right = null;
                    ret.add(root);
                }
            } else if (right!=null) {
                for(TreeNode rightnode:right) {
                    TreeNode root = new TreeNode(i);
                    root.left = null;
                    root.right = rightnode;
                    ret.add(root);
                }
            } else {
                TreeNode root = new TreeNode(i);
                root.left = null;
                root.right = null;
                ret.add(root);
            }
        }
        return ret;
    }

}

108.将有序数组转换为二叉搜索树

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

因为需要构建平衡的二叉搜索树，构建树时，选择数组最中间的数作为根节点，左右子树递归计算。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return dfs(nums,0,nums.length-1);
    }

    //前闭后闭
    public TreeNode dfs(int[] nums,int start,int end) {
        if(start>end) {
            return null;
        }
        int mid = (start+end)/2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = dfs(nums,start,mid-1);
        root.right = dfs(nums,mid+1,end);
        return root;
    }
}

173.二叉搜索树迭代器

实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。

调用 next() 将返回二叉搜索树中的下一个最小的数。

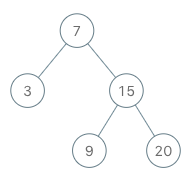
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // 返回 3
iterator.next();    // 返回 7
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 9
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 15
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 20
iterator.hasNext(); // 返回 false

二叉树的中序遍历即可将二叉搜索树中的数递增输出，因此本题将中序遍历拆解，一次输出一个。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class BSTIterator {

    Stack<TreeNode> stack;
    TreeNode curr;

    public BSTIterator(TreeNode root) {
        this.stack = new Stack<>();
        this.curr = root;
    }
    
    /** @return the next smallest number */
    public int next() {
        int ret=0;
        if(curr!=null || !stack.empty()) {
            while(curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            curr = stack.pop();
            ret = curr.val;
            curr = curr.right;
        }
        return ret;
    }
    
    /** @return whether we have a next smallest number */
    public boolean hasNext() {
        if(curr!=null || !stack.empty()) {
            return true;
        }
        return false;
    }
}

祖先问题

235.二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

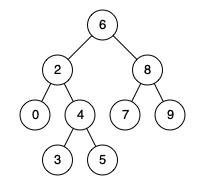
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

可以利用二叉搜索树的性质，知道p和q是否都在二叉树的左子树或右子树上，若是则递归求解左子树或右子树，否则当前根节点即为结果。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root.val > p.val && root.val > q.val) {
            return lowestCommonAncestor(root.left,p,q);
        } else if(root.val < p.val && root.val < q.val) {
            return lowestCommonAncestor(root.right,p,q);
        } else {
            return root;
        }
    }
}

236.二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]

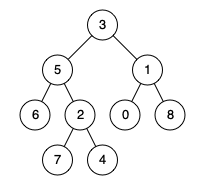
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

本题不能像二叉搜索树一样利用节点上的信息，但仍然可以使用递归求解。题解：【C++ 经典递归】思路非常好理解 时间复杂度O(n), 空间复杂度O(n)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) {
            return null;
        }
        if(root==p || root==q) {
            return root;
        }

        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left == null) {
            return right;
        }
        if (right == null) {
            return left;
        }
        if(left != null && right != null) {
            return root;
        }
        return null;
    }
}

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

leetcode树总结(python
weixin_42723548的博客
09-20 1062
做题顺序：144、94、145、102、103、96、95、98、100、101、111、105、106、108、104、110、111、112、113 牛客网【二叉树的下一个节点】 写递归循环的时候，先想基线条件是什么，也就是当只有最简单的情况时（当没有节点或只有一个节点的时候），怎么处理，再想递归条件是什么（当有两个节点或者三个节点的时候）。这样就很容易写出来了，树这里用了很多的递归，都要...
leetcode 树总结
李白-2017的博客
12-03 426
下面对leetcode中tree类下面的一些题目进行了总结，其中包括top 100 liked qusetions和top interviewquestions.   1.  二叉树的基本操作 find，insert(递归、非递归方法), create, delete. 删除的节点带有左右孩子，可以用直接前驱(被删除节点最右分支的节点)或是直接后继(被删除节点最左分支的节点)代替被删除节点
Leetcode总结（树）
Aaron_Marvel的博客
05-24 727
Leetcode刷题中的Tree类型，解析比较经典的题目
leetcode总结——树篇
weixin_45680007的博客
02-17 392
自上而下： 路径和sum 最短路径 镜像树 层次遍历 树化链表 完全二叉树的节点个数： 路径和sum： 给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。 说明: 叶子节点是指没有子节点的节点。 示例: 给定如下二叉树，以及目标和 sum = 22， 5 / \ 4 8 ...
LeetCode-树(解题技巧总结三)
qq_41605114的博客
05-01 359
五 递归再理解 894. 所有可能的满二叉树 https://leetcode-cn.com/problems/all-possible-full-binary-trees/ /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * ...
LeetCode解题总结
10-09
LeetCode解题总结 1. 数组 1.1 从有序数组中删除重复元素 1.2 在排序数组被旋转后进行查找 1.3 寻找两个排序数组的中位数 1.4 最长连续序列 1.5 累加和 1.6 移除数组中指定值 1.7 下一个排列 1.8 第n个全排列 1.9 ...
leetcode338-LeetCode:LeetCode刷题总结
07-01
LeetCode刷题总结 1.Two Sum 2.Add Two Numbers 3.Longest Substring Without Repeating Characters 4.Median of Two Sorted Arrays 5.Longest Palindromic Substring (Manacher算法待完成) 6.ZigZag Conversion 7....
Leetcode:LeetCode 刷题总结
05-11
7. **图论**：图论问题涉及节点和边的连接，如"最短路径"（Shortest Path）或"最小生成树"（Minimum Spanning Tree）。 8. **排序与查找**：快速排序、归并排序、二分查找等经典算法在LeetCode中也有体现，例如"三...
LeetCode-Learning:《LeetCode 刷题总结》
04-08
《LeetCode 刷题总结》是一份专注于 LeetCode 在线编程平台刷题经验与技巧的综合分析资源。LeetCode 是一个热门的在线平台，提供了一系列的编程挑战，旨在提升开发者们的算法技能、数据结构理解以及问题解决能力。...
leetcode二叉树相关操作的总结
ss654271961的博客
08-09 824
做了这么多关于二叉树的题，发现一些题目的本质来来回回就是那些操作，所以觉得需要进行总结，可以让之后的思路更明晰。 二叉树的操作，最普遍的就是递归，和前中后序遍历，层序遍历。前中后序遍历可以用递归也可以用自己的栈代替递归栈。层序遍历用一个队列辅助，每一层都是上一层所有节点的孩子。在这个过程中也可以记录每一层包含的节点及个数。 递归的解决问题的话，有三个要素：首先你要确定他们之间有递归关系，大规模
C语言实现二叉树的创建、插入、删除、遍历等操作
12-14
C语言实现二叉树的创建、插入、删除、遍历（先序、中序、后续、深度优先、广度优先）、计算度为0,1,2的节点个数。 包括排序二叉树的实现
树的总结--树的性质II leetcode
weixin_34283445的博客
01-06 111
Same Tree Given two binary trees, write a function to check if they are equal ornot. Two binary trees are considered equal if they are structurallyidentical and the node...
Leetcode树专题
三笔竹林的博客
02-27 927
树的常识 三种遍历方法 对应的数据结构 Leetcode257.Binary Tree Paths 思路：很典型的深度优先搜索配合栈，宽度优先搜索配合队列。学一个遍历二叉树的方法 Leetcode111. Minimum Depth of Binary Tree（求二叉树的最短深度） 较差的思路：从上题思路套用而来，先求得所有路径的节点数（就是长度），再求最小值 较好的思路：宽度优先搜...
Leetcode：200题总结(五)
平凡
02-23 371
718. Maximum Length of Repeated Subarray 给定两个序列，求同时出现在两个序列中的最长子列的长度。 思路：因为相同子列可以出现在两个序列的任意位置，所以比较直接的想法是用两个嵌套的循环实现对两个序列中元素的遍历，并且结合动态规划。 顺便记录一下二维数组的初始化方式：vector<vector<int>> dp(A.size()+1...
LeetCode上与树相关的问题
a novice
05-18 3960
前言没想到大三依然课业繁重，再加上一些琐事缠身，以及自身的惰性，不少计划都是心有余力不足，但又不愿这么混下去，近来回顾了一下自己在学习算法技能树上的加点，发现一些基础算法与经典算法实在是有那么点囫囵吞枣，所以有个刷leetcode的打算，一是为了温故知新，二是为了熟悉Java或Python，三是为了保持编程手感，四是为以后工作做个铺垫？目标大概是有生之年内用Java/Python/C++/C刷一遍l
leetcode在线编程【树专题】
kuronekonano的博客
03-23 425
二叉树的最小深度 递归遍历每个节点并计数深度，遍历到叶子节点时更新最小深度，并返回，非叶子节点取返回值的最小深度返回 class Solution { public: int ans=9999999; int dfs(TreeNode *root,int dep) { dep++; if(root->left==NULL&&am...
leetcode力扣刷题总结---树篇（交流学习）
Allen_Xu17
06-06 690
树是数据结构中很重要的一个主题，突破了以往线性结构的结构的限制，让数据的组织、存储和使用更加灵活。 与树息息相关的一个概念便是递归，理解和灵活运用递归，不仅能够突破对树的理解，更能方便我们理解和解决其他问题。 本篇总结是在学习了树相关基础知识的基础上，进行的刷题练习，希望能更加深入、灵活的掌握与树相关的知识。 有的解法是自己原创，有的是参考了优秀题解，欢迎交流！ ...
b树的构造c++_刷题-树的相关计算
weixin_39621488的博客
12-20 206
链表弄的有点明白后，我就想对树也速成一下。树一般都是迭代，我总是搞不清逻辑，不知道迭代终止条件咋写，以及，迭代中间的计算到底咋实现的。今天打算就补补树的逻辑。1.计算树的高度这是一棵树：正常情况下按照咱们大脑的想法：1）算 A 的左右子树高度，返回他俩中 最大的那个数，加上1返回。2）算 A 的 左子树高度，算 A 的右子树高度。3）A 的左子树 B 的高度 --> B 的左右子树高度，返回...
Leetcode刷题——树篇2
w137093940的博客
05-01 691
文章目录2、树（简单篇2）2.1、965. 单值二叉树2.1、 669. 修剪二叉搜索树2.3 102. 二叉树的层序遍历2.4 107. 二叉树的层次遍历 II2.5、 637. 二叉树的层平均值 2、树（简单篇2） 2.1、965. 单值二叉树 如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。 只有给定的树是单值二叉树时，才返回 true；否则返回 false。 示例 1： ...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值