机器学习训练营——机器学习爱好者的自由交流空间(入群联系qq:2279055353)
TF-idf 权
在大的文本合集里,一些词出现的频率很高(例如英文里的the, a, is)但包含的实际文本内容的有价值的信息却很少。如果我们把计数的数据直接提供给一个分类器,那些高频词条会影响罕见但更有意义的词条。为了重新加权计数特征为适合分类器使用的浮点值,现在普遍采用tf-idf变换。
tf的意思是term-frequency, 而tf-idf的意思是term-frequency times inverse document-frequency, 公式为:
tftftf-idf(t,d)=tf(t,d)×idf(t)idf(t, d)=tf(t, d)\times idf(t)idf(t,d)=tf(t,d)×idf(t)
这里,使用TfidfTransformer的默认设置,TfidfTransformer(norm='l2', use_idf=True, smooth_idf=True, sublinear_tf=False)
tf(t,d)tf(t, d)tf(t,d)表示词条频数,即,一个词条在一个给定文档里出现的次数。
idf(t)=log1+nd1+df(d,t)+1idf(t)=\log\dfrac{1+n_d}{1+df(d, t)}+1idf(t)=log1+df(d,t)1+nd+1
ndn_dnd表示文档总数,df(d,t)df(d, t)df(d,t)表示包含词条ttt的文档数,结果tf-idf向量经欧拉范数归一化
vnorm=v∣∣v∣∣2=vv12+v22+⋯+vn2v_{norm}=\dfrac{v}{||v||_2}=\dfrac{v}{\sqrt{v_1^2+v_2^2+\dots+v_n^2}}vnorm=∣∣v∣∣2v=v12+v22+⋯+vn2v
这个词条加权方案最初来自信息检索领域,后引入到文档分类、聚类问题,也得到好的效果。
下面我们进一步解释和举例说明tf-idf怎样精确地计算,以及使用TfidfTransformer, TfidfVectorizer计算tf-idf与标准定义的区别。idf的标准定义为
idf(t)=lognd1+df(d,t)idf(t)=\log \dfrac{n_d}{1+df(d, t)}idf(t)=log1+df(d,t)nd
在TfidfTransformer, TfidfVectorizer里,通过设置参数smooth_idf=False, 1被加到idf上,而不是标准定义的分母项。
idf(t)=lognddf(d,t)+1idf(t)=\log \dfrac{n_d}{df(d, t)}+1idf(t)=logdf(d,t)nd+1
然后,归一化由TfidfTransformer类执行:
from sklearn.feature_extraction.text import TfidfTransformer
transformer = TfidfTransformer(smooth_idf=False)
transformer

让我们用下面的counts举一个例子。第一项(列)出现频率100%, 所以意义不大,后两个向量出现频率低于50%, 故很可能是有代表性的文档内容。
counts = [[3, 0, 1],
[2, 0, 0],
[3, 0, 0],
[4, 0, 0],
[3, 2, 0],
[3, 0, 2]]
tfidf = transformer.fit_transform(counts)
tfidf
tfidf.toarray()
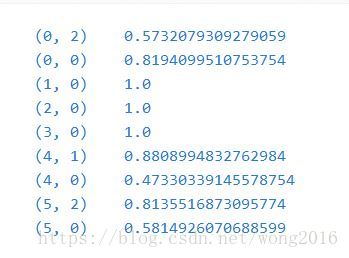

每一行被归一化为1范数。例如,我们可以按如下公式计算第一项在第一个文档里的tf-idf:
nd,term1=6n_{d, term1}=6nd,term1=6
df(d,t)term1=6df(d, t)_{term1}=6df(d,t)term1=6
idf(d,t)term1=lognddf(d,t)+1=log1+1=1idf(d, t)_{term1}=\log\dfrac{n_d}{df(d, t)}+1=\log1 + 1=1idf(d,t)term1=logdf(d,t)nd+1=log1+1=1
tftftf-idfterm1=tf×idf=3×1=3idf_{term1}=tf\times idf=3\times1=3idfterm1=tf×idf=3×1=3
现在,如果我们重复计算该文档剩余两项,则得到
tftftf-idfterm2=0×(log(6/1)+1)=0idf_{term2}=0\times (\log(6/1)+1)=0idfterm2=0×(log(6/1)+1)=0
tftftf-idfterm3=1×(log(6/2)+1)≈2.0986idf_{term3}=1\times (\log(6/2)+1)\approx2.0986idfterm3=1×(log(6/2)+1)≈2.0986
这样,原始tf-idf向量为[3, 0, 2.0986], 然后,按欧式(L2)范数,得到文档1的tf-idf:
[3,0,2.0986]32+02+2.09862=[0.819,0,0.573]\dfrac{[3, 0, 2.0986]}{\sqrt{3^2+0^2+2.0986^2}}=[0.819, 0, 0.573]32+02+2.09862[3,0,2.0986]=[0.819,0,0.573]
进一步,缺省参数smooth_idf=True对分子分母分别加1,好像存在一个外部文档,包含每一个词条,这样避免了分母是0的情况。
idf(t)=log1+nd1+df(d,t)+1idf(t)=\log\dfrac{1+n_d}{1+df(d, t)}+1idf(t)=log1+df(d,t)1+nd+1
使用这个修正,文档1的第三项的tf-idf修正为:
tftftf-idfterm3=1×log(7/3)+1≈1.8473idf_{term3}=1\times \log(7/3)+1\approx 1.8473idfterm3=1×log(7/3)+1≈1.8473
这样,经L2归一化的tf-idf修正为
[3,0,1.8473]32+02+1.84732=[0.8515,0,0.5243]\dfrac{[3, 0, 1.8473]}{\sqrt{3^2+0^2+1.8473^2}}=[0.8515, 0, 0.5243]32+02+1.84732[3,0,1.8473]=[0.8515,0,0.5243]
transformer = TfidfTransformer()
transformer.fit_transform(counts).toarray()
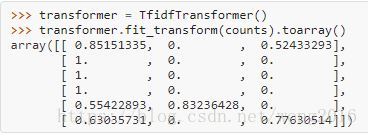
经fit方法计算的每个特征的权保存在一个模型属性里。
transformer.idf_

由于tf-idf经常用于文本特征数量化,也有另一个类TfidfVectorizer结合CountVectorizer, TfidfTransformer所有的选项在一个模型里:
from sklearn.feature_extraction.text import TfidfVectorizer
corpus = [
'This is the first document.',
'This is the second second document.',
'And the third one.',
'Is this the first document?',
]
vectorizer = TfidfVectorizer()
vectorizer.fit_transform(corpus)

阅读更多精彩内容,请关注微信公众号:统计学习与大数据




 TF-IDF是一种常用的文本特征权重计算方法,它能够降低高频词汇的影响,突出重要词汇。本文深入讲解TF-IDF的计算原理,包括其在`sklearn`中的实现,并通过实例展示了如何进行归一化处理,以提升模型的性能。
TF-IDF是一种常用的文本特征权重计算方法,它能够降低高频词汇的影响,突出重要词汇。本文深入讲解TF-IDF的计算原理,包括其在`sklearn`中的实现,并通过实例展示了如何进行归一化处理,以提升模型的性能。
















 1182
1182

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








