工业机器人各种坐标

 1、名词：

关节：各机械轴

关节空间：对于一个具有n个自由度的的操作臂来说，它的所有连杆位置可由一组n个关节变量来确定。这样的一组变量通常被称为n x 1的关节矢量。所有关节矢量组成的空间称为关节空间。

笛卡尔坐标系：在数学里，笛卡尔坐标系 (Cartesian coordinate system)，亦称直角坐标系，是一种正交坐标系

笛卡尔空间：当位置是在空间相互正交的轴上的测量，且姿态是按照空间描述章节中任一一种规定测量的时候，我们称这个空间为笛卡尔空间，有时也称为任务空间或者操作空间。简单地理解成在空间直角坐标系。

位姿表示：位姿代表位置和姿态。

任何一个刚体在空间坐标系(OXYZ)中可以用位置和姿态来精确、唯一表示其位置状态。

• 位置：x、y、z坐标
• 姿态：刚体与OX轴的夹角rx、与OY轴的夹角ry、与OZ轴的夹角rz

        机器人运动学中碰到的第一个问题---正运动学问题。也就是在已知机器人各个关节的位置的情况下确定其末端执行器的位置。即如果我们知道机器人各个关节当前旋转的角度，如何确定P点在坐标系{A}中的坐标P(x,y,z)呢？

2、位置与姿态

2.1位置

如下图所示，两个坐标系{A}和{B}的坐标轴分别平行，设坐标系{A}为基坐标系，那么如何表达坐标系B与坐标系A关系呢？

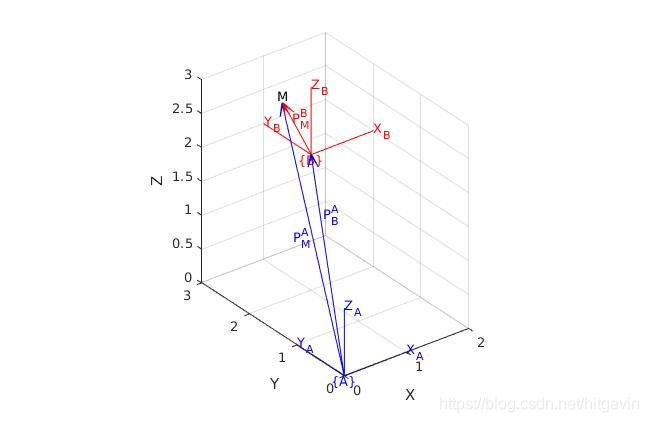
 从图中我们知道，空间中任意一点M在基坐标系{A}中的位置可以用向量表示，而在坐标系{B}中可以用向量表示。坐标系{B}的原点可以用向量表示（注意这些记法的上标代表该向量在哪个坐标系中表达，也就是向量的起点与哪个坐标系的原点重合，下标代表的是空间中的点，比如M代表的是M点。因此代表X点在坐标系Y下的向量表示）。根据向量的运算法则，我们很容易得到下面的等价关系

                                                                                 

在上面的等式中和都代表了点M的坐标，只是参考坐标系不同，一个参考系是坐标系{A}，一个参考系是坐标系{B}。那么又代表了什么呢？我想你应该能够想到这个代表了两个坐标系之间的位置关系。因此对于只存在平移关系的两个坐标系，我们通过一个三维向量就可以描述坐标系{B}与坐标系{A}的关系。上面的等式也就是在只有平移的情况下点在坐标系{A}与{B}之间的坐标变换公式。

2.2姿态（旋转）

旋转的描述是比较复杂的，我们先讨论只有旋转，没有平移的情况，即两个坐标系原点重合的情况。如下图所示，在这样的情况下怎么去描述坐标系{B}与坐标系{A}之间的关系呢？

3、坐标系

       

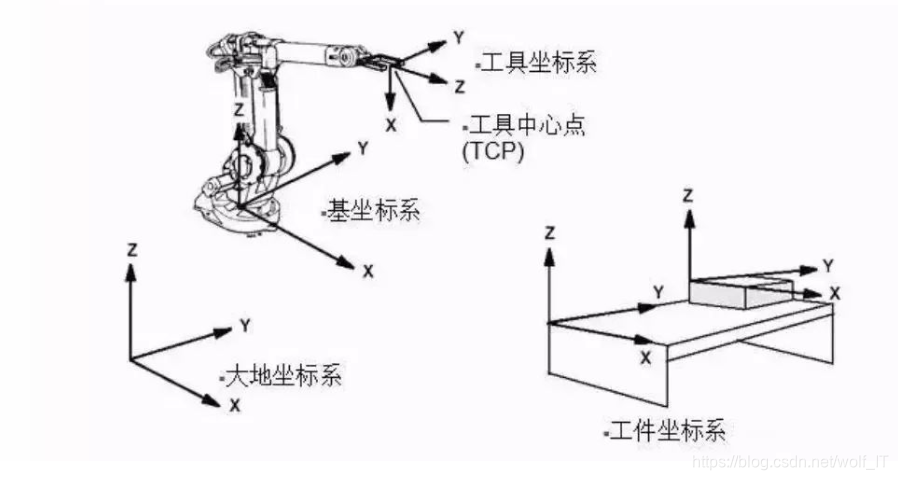
工业机器人上的坐标系包括六种：

大地坐标系（World Coordinate System）

基坐标系（Base Coordinate System）

关节坐标系(Joint Coordinate System)

工具坐标系（Tool Coordinate System）

工件坐标系（Work Object Coordinate System）

用户坐标系(User Coordinate System)

3.1. 大地坐标系

　　大地(世界)坐标系是固定在空间上的标准直角坐标系，它被固定在事先确定的位置。用户坐标系是基于该坐标系而设定的。

　　3.2.基坐标系

　　基坐标系由机器人底座基点与坐标方位组成，该坐标系是机器人其它坐标系的基础。

　　3. 3关节坐标系

　　关节坐标系是设定在机器人关节中的坐标系，它是每个轴相对其原点位置的绝对角度。

       3.4. 工具坐标系

　　工具坐标系用来确定工具的位姿，它由工具中心点(TCP)与坐标方位组成。工具坐标系必须事先进行设定。在没有定义的时候，将由默认工具坐标系来替代该坐标系。

      工具坐标系可采用N(N＞＝4)点法确定：机器人TCP通过N种不同姿态同某定点相接触，得出多组解，通过计算得出当前TCP与工具安装法兰中心点(tool0)的相应位置，坐标系方向与tool0一致。

 

 

3.5. 工件坐标系

　　工件坐标系用来确定工件的位姿，它由工件原点与坐标方位组成。工件坐标系可采用三点法确定：点X1与点X2连线组成X轴，通过点 Y1向X轴作的垂直线为Y轴，Z轴方向以右手定则确定。

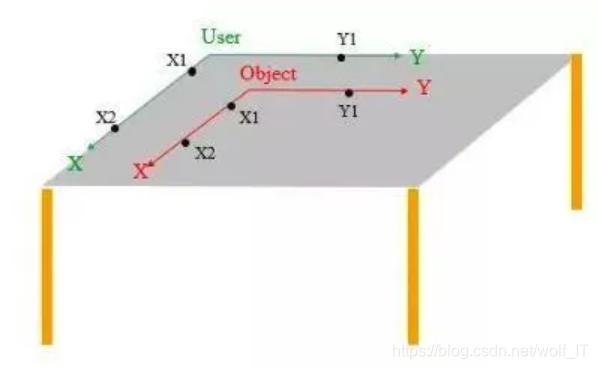
3.6. 用户坐标系

　　用户坐标系是用户对每个作业空间进行自定义的直角坐标系，它用于位置寄存器的示教和执行、位置补偿指令的执行等。在没有定义的时候，将由大地坐标系来替代该坐标系。