注:该算法已按照智能优化算法APP标准格式进行整改,可直接集成到APP中,方便大家与自己的算法进行对比。(近期智能优化算法APP将会迎来超级大更新!请时刻保持关注哦!)
向光生长算法(Phototropic Growth Algorithm, PGA)是一种受到植物向光性生长机制启发的智能优化方法。在自然界中,植物依靠体内生长素的分布调节,主动朝向光源生长,以最大化光合作用效率,展现出令人惊叹的环境适应能力。科研人员正是借助这一生物行为特征,提出了PGA算法,模拟植物在光照引导下的三大关键策略:趋光性定向生长、自适应分枝调节机制,以及在资源受限环境中的探索式延展过程。这些策略被巧妙抽象为数学模型,有效融合全局探索与局部开发能力,使 PGA 在求解复杂、多约束优化问题中展现出卓越的解质量。
该成果于2025年7月最新发表在计算机领域一区期刊Knowledge-Based Systems上,具有出色的应用前景。

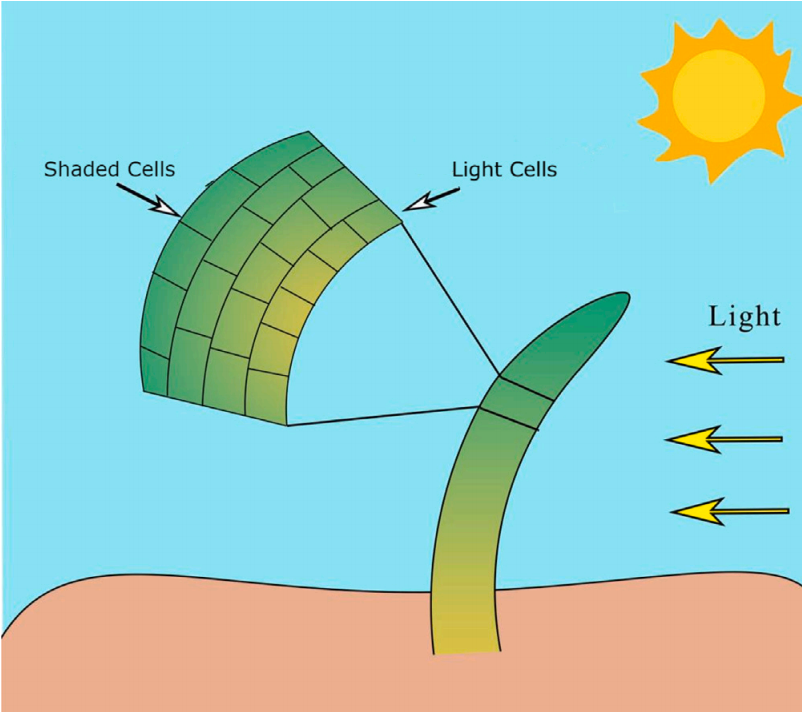
为了在多变的环境条件下实现最优生长和发育,植物进化出多种机制,其中之一即为向光性。向光性是指植物对光源发生趋向或背离的定向生长反应。该响应对于植物适应光照变化、最大化光合作用至关重要。向光性涉及多个生理过程,主要包括细胞分裂和细胞伸长的变化。下图所示的有丝分裂过程在向光性中起着关键作用,它通过产生能够朝向光源伸长的新细胞来实现定向生长。有丝分裂是指细胞分裂为两个完全相同的子细胞的过程。

细胞伸长是植物生长与发育中的另一个关键过程。当光线照射植物的一侧时,生长素会在阴影一侧积聚,从而使该区域的细胞比光照区域的细胞伸长得更快。由此,阴影区域生长更快,导致植物向着光源方向弯曲。下图展示了细胞伸长的过程,其中阴影区域的细胞更快地伸长,使植物向光倾斜。
1 算法原理详解
(1)初始化
该算法首先初始化一个由细胞组成的种群,记作集合 ,这些细胞也被视为搜索代理。在算法中,光照对细胞行为的影响具有核心地位。因此,种群被划分为两个区域:光照区域 和阴影区域 ,分别表示接受良好光照的细胞与处于遮蔽位置的细胞。处于光照区域的细胞数量 由区间 内的一个随机值控制, 与 为该比例的上下限。该值通过公式 生成,其中 是在 范围内均匀分布的随机变量。此设定确保 在整体种群 中所占比例合理受限于指定区间。
为了将该比例转换为具体的细胞数量,需要将其乘以总种群规模 。然而,该操作可能产生一个小数,而当 表示具体细胞数时,小数并无实际意义。因此,引入下取整函数以将结果向下取整至最接近的整数。计算 的最终公式如下所示:
在确定 之后,算法继续将解集合 中的前 个个体指定为处于光照区域的细胞(记为 )。该子集的数学表示如下:
阴影区域的细胞数量 等于总细胞数 减去光照区域细胞数 ,其表达式为:
阴影区域的细胞集合 是解集 的子集,可定义为:
(2)光照区细胞的有丝分裂
为了对有丝分裂过程进行数学建模,种群中的每个细胞都会分裂成两个子细胞,这一母细胞分裂成两个子细胞的现象称为有丝分裂。变异算子是生成子细胞多样性的关键组成部分。该算子应用于第一个复制体,并相对于从种群中随机选取的细胞进行计算。通过随机选择细胞的方法,此方法准确模拟了由于辐射或化学物质等环境因素引起的变异的随机性,保证变异算子具有广泛的可能结果:
在许多生物系统中,生长和适应速率在初期通常较为强劲,但随着时间推移逐渐减弱。例如,细胞生物学表明,细胞在早期阶段经历快速生长和分裂,但随着成熟临近,这种迅猛的增长速度会减缓,这通常归因于资源限制、环境压力以及细胞的内在老化过程。受此启发,算法采用指数衰减函数𝛼来模拟这一自然演变过程。此行为的数学表达见以下公式:
此方程基于指数衰减函数的标准形式推导而来,通常表示为:
其中,𝐴为初始值,𝑘为衰减常数,𝑡为时间。
基因突变中的内在随机性体现了自然界的适应策略。尽管突变遵循一定模式,但其不可预测性确保了物种能够应对未知挑战。算法中的𝑟2和𝑟3项即反映了这种生物随机性。定义为 ,其取值范围为−1到1,允许突变既可增强也可减弱,体现了突变的双重特性:部分有益于生存,部分则可能有害。为更好理解,考虑有丝分裂的生物学表达:
变异项是引入多样性的重要组成部分,其数学表达式为:
针对光照区域细胞的变异算子 是所提优化算法的重要组成部分。它模拟了变异的随机性和多样性,保证了解空间的广泛多样性。引入随机变异因子 和生长限制因子 ,使得变异算子在不同环境条件下表现出强大的鲁棒性和适应性。
为了数学地描述这一行为,生长素重分布算子计算当前光照细胞相对于最佳光照细胞的位移,记作 。该位移通过当前细胞与最佳光照细胞的位置差进行建模,并乘以代表生长素影响和光照强度的调节因子。基于新细胞位置 受当前细胞 与最佳光照细胞 之间差异影响的基本假设,可表示为:
然而,这一位置差异 需要通过若干因子进行调节,以体现生长素的影响及生物过程中的内在随机性。生长限制因子 代表生长素的作用,而 引入了随机成分,反映了生物过程中的不确定性。结合这些因子后,调节后的位置偏移可表示为:
最后,新细胞的位置 由当前位置与经过调节的位移相加得到:
为了确定 ,可以借鉴之前定义的随机变量 和 。由于它们被定义为 ,使其取值范围在 之间, 也可类似定义为:
该取值范围使该算子能够同时考虑正向和负向的变化,模拟植物细胞中生长素的双向调控作用。该公式虽具数学结构性,但实质体现了自然界“适应与优化”的核心策略。考虑到细胞随着成熟对生长变化的敏感度降低,通过逐渐减小的生长限制因子 体现,随着时间推移, 下降,从而限制了允许的生长变化幅度。这种设计能够模拟细胞过程中的内在随机性,更真实地反映细胞对光照的响应行为。
(3)阴影区域细胞的有丝分裂
本节介绍了用于更新阴影区域细胞 的两种主要变异算子。该类变异算子的目标是模拟植物在生长和发育过程中,因环境因素而产生的变化。变异算子:作用于第一份有丝分裂副本。用于更新 的第一变异算子形式上与 的更新公式类似,这是因为阴影区域细胞的变异主要归因于遗传因素。该变异算子的更新公式如下所示:
此处, 的计算方式与 类似。该算子的整体作用在于引入独立于物理条件的阴影区细胞变异。生长素重分布算子是用于更新 值的第二种突变算子。该算子通过模拟光照条件差异下生长素从光照细胞向阴影细胞的再分配过程,推动阴影细胞的生长,从而使植物向光弯曲。根据当前最优光照细胞 来计算该变化量,变化量通过随机突变因子 进行缩放以模拟随机变化,同时通过生长限制因子 控制允许的生长变化幅度。生长素重分布算子的更新公式如下所示:
其中, 是一个在区间 之间的随机数。由上述两种突变算子生成的新细胞将被追加到当前解集(即 )中。随后,根据适应度值对所有解进行评估,并剔除最差的解。该机制确保了解集的规模保持不变,且仅保留适应度最高的细胞参与后续进化过程。
在算法的第二阶段,考虑了生长素对细胞伸长的影响。生长素是一类植物激素,参与调控植物体内多种生长与发育过程,尤其在细胞沿植物轴向方向的生长调控中发挥着关键作用。当植物暴露于不均匀的光照条件下时,生长素的分布将出现差异化。结果是,处于阴影区域的细胞比位于光照区域的细胞具有更高浓度的生长素。阴影区细胞中较高的生长素浓度会导致其细胞伸长程度大于光照区的细胞,从而使植物茎尖朝向光源发生弯曲。这一适应机制对于植物最大化光照利用、促进生长与生存具有重要意义。在细胞伸长阶段,算法引入了细胞的弯曲现象及其弯曲因子,以模拟细胞在搜索空间中的运动行为。
在弯曲度的计算中,优先考虑光照区域的细胞。植物细胞的弯曲度可通过公式进行计算:
其中, 是一个自适应参数,用于在算法初期支持搜索空间的探索行为,在后期则促进对最优解的开发(利用); 是方向切换系数,赋予了移动过程中的灵活性,模拟了现实世界中的变异性。
弯曲因子受光照强度的影响。在求解实际优化问题时,本文所提出的算法将当前最优适应度解视为光源,所有细胞会趋向该最优解发生弯曲。弯曲因子( )的计算方式如公式所示:
其中, 是一个位于区间 (−1, 1) 内的随机数。术语 确保每个细胞朝着当前最优解的方向移动,从而模拟植物的向光弯曲响应;同时,随机数 引入了受控的随机性。
除了曲率因子之外,细胞邻域在决定细胞伸长的程度上也起着关键作用。一个细胞是否处于光照区或阴影区,可以通过其周围的细胞来推断。从物理上看,阴影区的细胞往往彼此靠近,而光照区的细胞则相对分散。细胞邻域项考虑了相邻细胞的影响,并通过因子 进行缩放,以限制成熟细胞随时间发生的变化幅度;同时通过 体现细胞在感知生长素过程中的随机性。细胞邻域的计算公式如下所示:
其中, 是一个取值范围在 内的随机数。因此,每个细胞在“细胞伸长阶段”的更新公式如下所示:
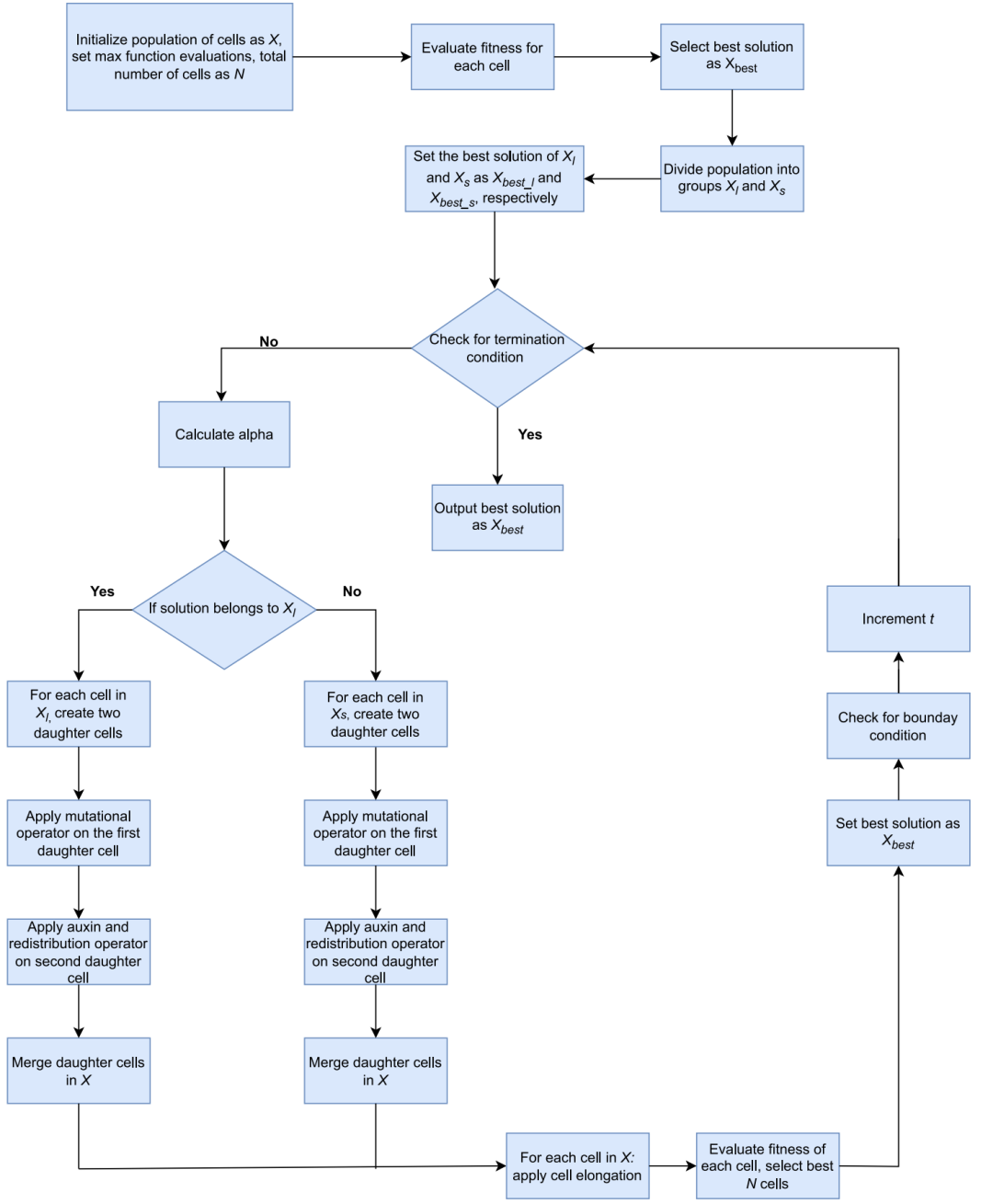
PGA优化算法的流程图如下所示:
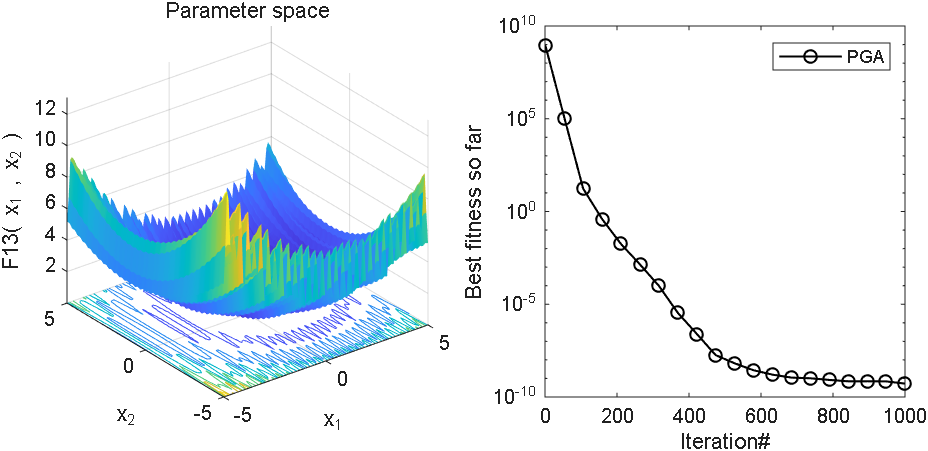
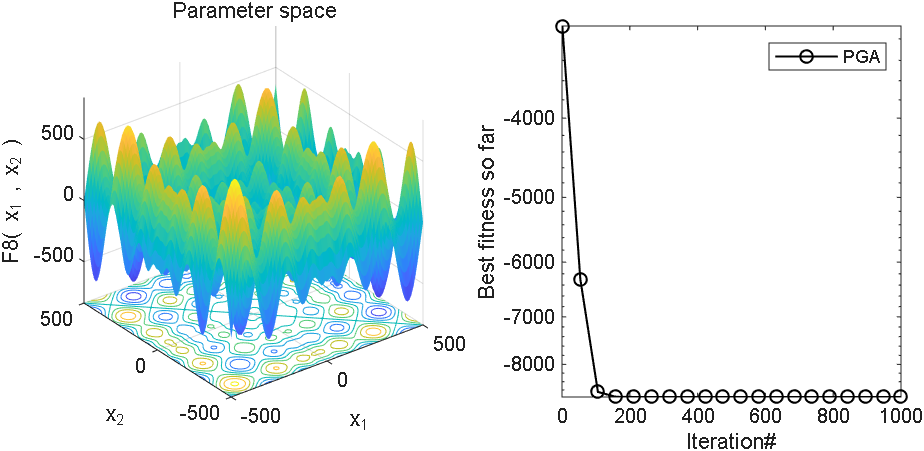
2 结果展示
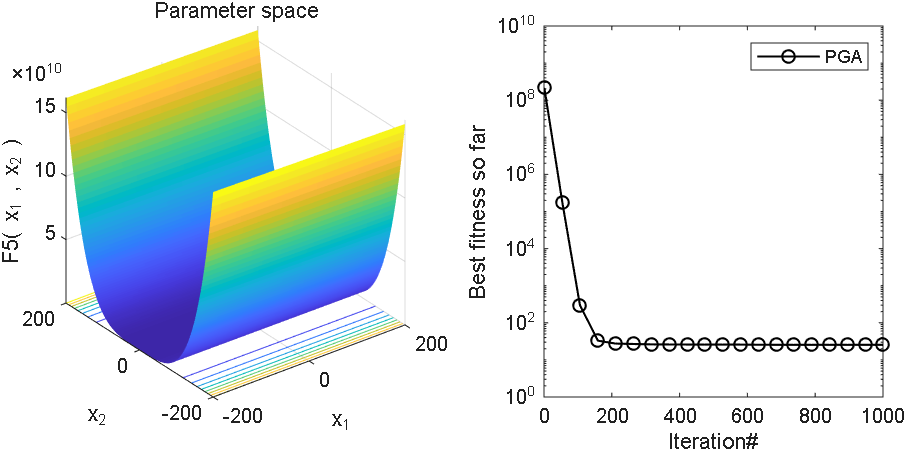
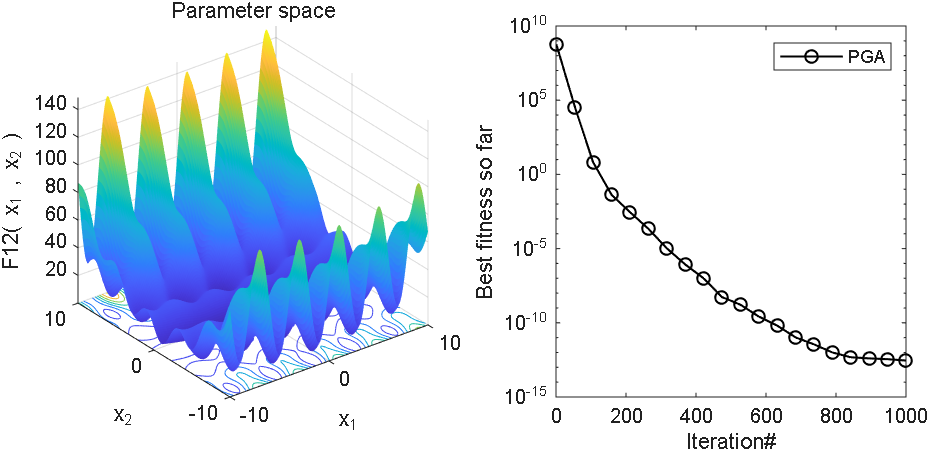
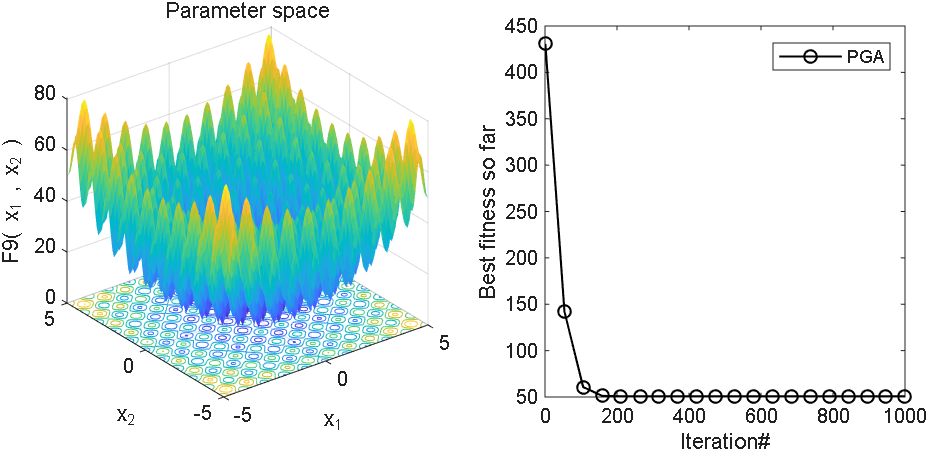
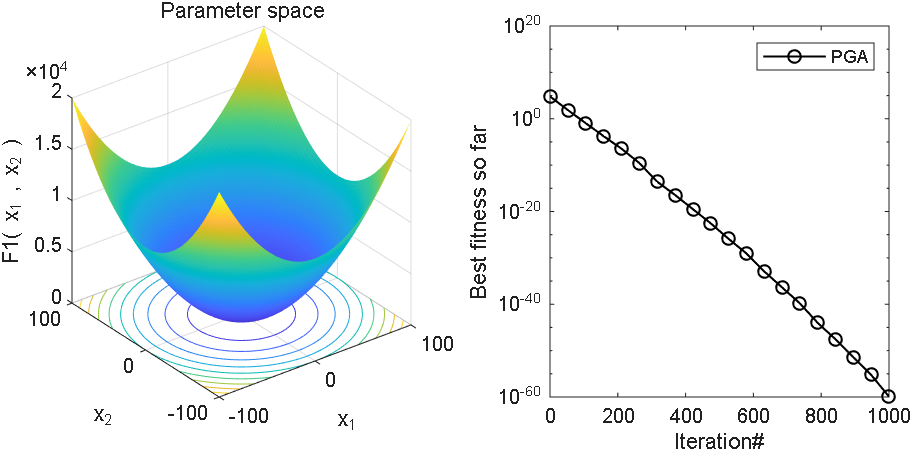
3、MATLAB核心代码
3、MATLAB核心代码
%% 淘个代码 %%
% 微信公众号搜索:淘个代码,获取更多代码
% 向光生长算法(Phototropic Growth Algorithm, PGA)
function [Fbest,Xbest,CNVG]=PGA(N,T,lb,ub,dim,fobj,nn)
% initialise the best cell
Fbest=inf;
vec_flag=[1,-1];
Nl=round((0.2*rand+0.4)*N);%eq.(2&3)
%Initialise the plant cells
X=initialization(N,dim,ub,lb);
for i=1:N
fitness(i)=feval(fobj,X(i,:)',nn);
end
[GYbest, gbest] = min(fitness);
Xbest= X(gbest,:);
Ns=N-Nl;
Xs=X(1:Ns,:);
Xl=X(Ns+1:N,:);
% Initialisng fitness variables
fitness_s=fitness(1:Ns);
fitness_l=fitness(Ns+1:N);
[fitnessBest_s, gbest1] = min(fitness_s);
Xbest_s = Xs(gbest1,:);
[fitnessBest_l, gbest2] = min(fitness_l);
Xbest_l = Xl(gbest2,:);
Curvaure=1;
% ConcS=Curvaure*(mean(Xs)./Xbest_s).*(mean(fitness_s)/fitnessBest_s);
% ConcL=Curvaure*(mean(Xl)./Xbest_l).*(mean(fitness_l)/fitnessBest_l);
t=0; % Loop counter
while t<T
alpha = exp(-1*t/T); % eq(5)
for i=1:size(Xs,1)
FU=Xs(i,:)>ub;
FL=Xs(i,:)<lb;
Xs(i,:)=(Xs(i,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
fitness_s(i) = feval(fobj,Xs(i,:)',nn);
if fitness_s(i)<fitnessBest_s
fitnessBest_s=fitness_s(i);
Xbest_s=Xs(i,:);
end
end
for i=1:size(Xl,1)
FU=Xl(i,:)>ub;
FL=Xl(i,:)<lb;
Xl(i,:)=(Xl(i,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
fitness_l(i) = feval(fobj,Xl(i,:)',nn);
if fitness_l(i)<fitnessBest_l
fitnessBest_l=fitness_l(i);
Xbest_l=Xl(i,:);
end
end
flag_index = floor(2*rand()+1);
beta=vec_flag(flag_index);
Curvaure=beta*(alpha-mean(fitness_s)/Fbest); %Eq(17)
for i=1:size(Xl,1)
r2=2*rand(1,dim)-1;
r3=2*rand(1,dim)-1;
r4=2*rand(1,dim)-1;
dd=randi([1,N]);
flag_index = floor(2*rand()+1);
beta=vec_flag(flag_index);
Xlnew1(1,:)=X(dd,:)+beta*alpha.*r2.*abs(X(dd,:)-Xl(i,:))+beta*alpha.*r3.*abs(Xbest_l-Xl(i,:));%Eq(9)
Xlnew1(2,:)=Xl(i,:)+alpha.*r4.*abs(Xbest_l-Xl(i,:));%Eq(13)
for j=1:2
Tp=Xlnew1(j,:)>ub;Tm=Xlnew1(j,:)<lb;Xlnew1(j,:)=(Xlnew1(j,:).*(~(Tp+Tm)))+ub.*Tp+lb.*Tm;
fitness_lNew(j)=feval(fobj, Xlnew1(j,:)',nn);
end
Xl=[Xl; Xlnew1];
fitness_l=[fitness_l fitness_lNew];
end
for i=1:size(Xs,1)
r=2*rand(1,dim)-1;
flag_index = floor(2*rand()+1);
beta=vec_flag(flag_index);
Xsnew1(1,:)=Xs(i,:)+beta*alpha.*r.*abs(Xs(i,:)-X(randi([1,N]),:));% Eq(15)
Xsnew1(2,:)=Xl(randi(Ns),:)+beta*alpha.*r.*(Xbest_l-Xs(i,:));%% Eq(16)
for j=1:2
Tp=Xsnew1(j,:)>ub;Tm=Xsnew1(j,:)<lb;Xsnew1(j,:)=(Xsnew1(j,:).*(~(Tp+Tm)))+ub.*Tp+lb.*Tm;
fitness_sNew(j)=feval(fobj, Xsnew1(j,:)',nn);
end
Xs=[Xs; Xsnew1];
fitness_s=[fitness_s fitness_sNew];
end
[fitness_s, SortOrder]=sort(fitness_s);
Xs=Xs(SortOrder,:);
[fitnessBest_s,Sbest]=min(fitness_s);
Xbest_s=Xs(Sbest,:);
Xs=Xs(1:Ns,:);
fitness_s=fitness_s(1:Ns);
[fitness_l, SortOrder]=sort(fitness_l);
Xl=Xl(SortOrder,:);
[fitnessBest_l,lbest]=min(fitness_l);
Xbest_l=Xl(lbest,:);
Xl=Xl(1:Nl,:);
fitness_l=fitness_l(1:Nl);
if fitnessBest_l<Fbest
Fbest=fitnessBest_l;
Xbest=Xbest_l;
elseif fitnessBest_s<Fbest
Fbest=fitnessBest_s;
Xbest=Xbest_s;
end
X=[Xs;Xl];
fitall=[fitness_s fitness_l];
for i=1:N
r=2*rand(1,dim)-1;
flag_index = floor(2*rand()+1);
beta=vec_flag(flag_index);
FOC=r.*(Curvaure.*X(i,:)-Xbest); %eq(18)
Cell_vicinity=beta*alpha.*r.*(X(i,:)+X(i+1,:))/2; %eq(19)
Xnew(1,:)=X(i,:)+FOC+Cell_vicinity; %eq(20)
for j=1:1
Tp=Xnew(j,:)>ub;Tm=Xnew(j,:)<lb;Xnew(j,:)=(Xnew(j,:).*(~(Tp+Tm)))+ub.*Tp+lb.*Tm;
fitnessn(j)=feval(fobj, Xnew(j,:)',nn);
end
X=[X; Xnew];
fitall=[fitall fitnessn];
end
[fitall, SortOrder]=sort(fitall);
X=X(SortOrder,:);
[Fbest,best]=min(fitall);
Xbest=X(best,:);
X=X(1:N,:);
Nl=N-Ns;
Xs=X(1:Ns,:);
Xl=X(Ns+1:N,:);
fitness_s=fitness(1:Ns);
fitness_l=fitness(Ns+1:N);
[fitnessBest_s, gbest1] = min(fitness_s);
Xbest_s = Xs(gbest1,:);
[fitnessBest_l, gbest2] = min(fitness_l);
Xbest_l = Xl(gbest2,:);
% Update iteration counter
t=t+1;
CNVG(t)=Fbest;
end
end参考文献
[1] Bohat V K, Hashim F A, Batra H, et al. Phototropic growth algorithm: A novel metaheuristic inspired from phototropic growth of plants[J]. Knowledge-Based Systems, 2025, 322: 113548.
完整代码获取
后台回复关键词:
TGDM869
获取更多代码:

或者复制链接跳转:https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu




















 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










