雪雁优化算法，MATLAB代码免费获取

最新推荐文章于 2026-01-08 22:28:34 发布

原创最新推荐文章于 2026-01-08 22:28:34 发布 · 1.3k 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #matlab #开发语言

注：该算法已按照智能优化算法APP标准格式进行整改，可直接集成到APP中，方便大家与自己的算法进行对比。

雪雁算法（snow geese algorithm，SGA）是一种新型的启发式算法，该算法从雪雁在秋季和冬季的集体长途迁徙中汲取灵感，根据独特的人字形和直线形，以指导其探索和开发阶段。雪雁作为候鸟，在越冬地和繁殖地之间的运动表现出显着的规律性，与季节的变化保持一致。利用这种独特的行为，本文建立了一个强大的数学模型，并设计了一个算法的SGA过程。

该成果于2024年发表在工程领域2区期刊Applied Mathematical Modelling上，目前被引高达53次。

1.原理详解

(1)分类和定义

在提出的SGA中，假设每只雪雁代表给定优化问题的潜在解决方案。该问题的变量与这些雪雁在搜索空间内的空间位置相关联。因此，雪雁可以调整它们的位置，从而在各种维度中迁移，包括一维、二维、三维，甚至延伸到高维空间。由于SGA是一种基于种群的算法，本文采用位置矩阵P来表示雪雁种群的空间位置，使用速度矩阵V来表示雪雁在种群内的速度，简洁地表示如下：

其中，变量 n 表示种群中雪雁的总数，而 d 对应于与优化问题相关的变量数。

对于种群中的每只雪雁，它还必须假设存在一个数组 FV，该数组负责存储与每只雪雁的位置相关的适应度值，如下所示：

在这种情况下，必须强调适应度函数作为一个黑盒运行。所需要做的就是输入每只雪雁表示的候选解，这将产生一个输出即每只雪雁的适应度函数值。通过将每只雪雁的位置向量（表示为矩阵 P 中的第 i 个位置向量，其中0 <i ≤ n）馈送到适应度函数中，得到的数值将存储在向量 FV 中的相应位置。

SGA 是一个三元组，旨在逐步接近优化问题的全局最优值，表示为 SGA =（R， U， T）。在这个框架中，R 是一个函数，负责生成雪雁种群中每个个体的位置、速度和适应度值。

功能 U 的主要作用是不断调整个体在种群中的位置，旨在接近全局最优值。元启发式算法研究的核心是函数 U 的定义，重点是探索和开发过程的设计。探索阶段旨在确保对整个解决方案空间进行彻底探索，而开发阶段的目标是在候选者接近全局最优时收敛。此外，在设计函数 U 时，必须考虑与局部最优相关的挑战。在这种情况下，雪雁采用两阶段飞行策略，从人字形探索开始，过渡到直线队形开发。在勘探阶段，雁群频繁的位置变化使全面的路线探索成为可能，以适应不断变化的环境条件。

在这项研究中，SGA引入了一个超参数θ，用于表示雪雁种群从勘探阶段（探索阶段）到开发阶段（开发阶段）的转变。θ 可以用以下公式表示：

其中，M 代表函数 T 设置的最终评估标准。只要函数U执行的迭代满足t ≤ M，SGA将继续运行。若迭代次数超过M，则 SGA 算法会停止执行。

(2)人字形（探索阶段）

在雪雁的迁徙过程中，空气阻力和能量消耗等因素显著影响其飞行动力学。雁群的能量水平最初上升，随后随着接近目的地逐渐下降。为了简化分析，本文忽略了重力的影响。在飞行动力学的框架下，本文使用公式来表示速度变化。该公式表明，下一代速度取决于当前速度加速度 a 和时间步长 Δt

在SGA的背景下，必须仔细考虑每只雪雁速度矩阵的演变。在算法研究中，当前速度的大小对后续代的变化具有显著影响。因此，本文引入了一个权重因子c来表示这一过程。此外，变量Δt用于表示相邻代之间的差异，为了简化计算，将其值设为1。经过调整后的速度更新过程可以通过以下公式表示：

上述公式解释了连续代之间速度变化的模式，其中 c 捕捉了当前代与前一代速度之间的平衡。在雪雁群体的飞行过程中，它们的集体能量最初会增加，然后逐渐下降，直到达到一个收敛的位置。与这些行为特征相一致，SGA 中的速度调整过程也反映了类似的波动。用于这一调整过程的公式如下所示。

其在整个迭代过程中的演变在下图中得到了直观展示。

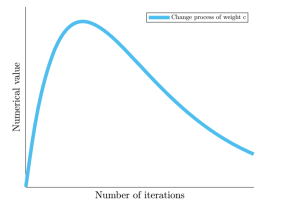
在雪雁的飞行过程中，需要考虑两个基本因素：它们遇到的空气阻力和固有的飞行能量。根据牛顿第二定律，SGA 使用公式。如前所述，SGA 模型中的雪雁被视为无质量的质点，因此本文在公式中忽略了个体质量 m，假设其为 1。

SGA 将雪雁的固有能量表示为 F。该能量定义为当前迭代中最佳位置与单个雪雁位置之间的差值，数学表达式为。借鉴牛顿第二定律，SGA 考虑了雪雁在飞行过程中遇到的空气阻力，这一过程的计算公式如下：

在这种情况下，有几个关键变量需要考虑。雪雁相对于流体的相对速度用V表示，阻力系数用C表示，A则代表相关的横截面积。阻力系数和面积受到雪雁夹角的影响。考虑到这些因素，可以制定以下公式：

此外，考虑到当前迭代中的最优解位置和当前雪雁位置，同时考虑空气阻力的影响，可以将加速度a表示为如下公式：

下图展示了整个雪雁种群中个体的分布。在整个优化过程中，更新雪雁位置时遵循特定的程序。

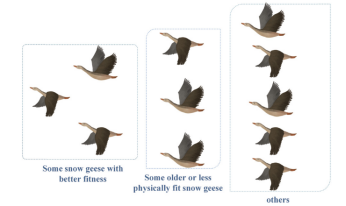
对于表现出卓越适应度值的前五分之一个体，使用公式进行位置更新：

对于种群中间部分的个体，包括那些较弱、生病或虚弱的个体（构成适应度最差的五分之一），使用公式进行位置更新：

最后，对于种群中剩余的个体，使用下式进行位置更新。这些不同的公式使本文能够根据个体的适应度水平调整雪雁的位置，确保优化过程能够适应种群中雪雁的不同能力和状态。

不同类别的雪雁使用不同的更新公式来调整它们的位置。值得注意的是，公式中的各个组件共同构成了最终的位置位移，每个组件都需要权重系数来表示其对整体公式的贡献。在SGA的背景下，这些权重系数通过公式来确定。其中，变量b、d和e对应于实验得出的经验值。变量Pc表示种群中中央粒子的位置，而表示与第i个粒子相关的适应度值。表示在种群排序后，最低排名雪雁的位置对应的候选解位置。

(3)直线形状（开发阶段）

当雪雁之间的角度超过Π时，它们进入飞行的第二阶段。在这个阶段，算法优先考虑逃避局部最优解，而非精确导航。雪雁采用直线飞行模式，并采取两种策略。

其中， ⊕ 表示逐项乘法。

集体引导：如果随机数 r > 0.5，雪雁会跟随经验丰富且身体强壮的同伴，集体寻找最优目标。

随机行为：当 r ≤ 0.5 时，雪雁表现出类似布朗运动的随机行为，以帮助其逃脱局部最优解。

2.结果展示

老规矩，采用作者独创的
智能优化算法APP轻松对比一下本期算法。

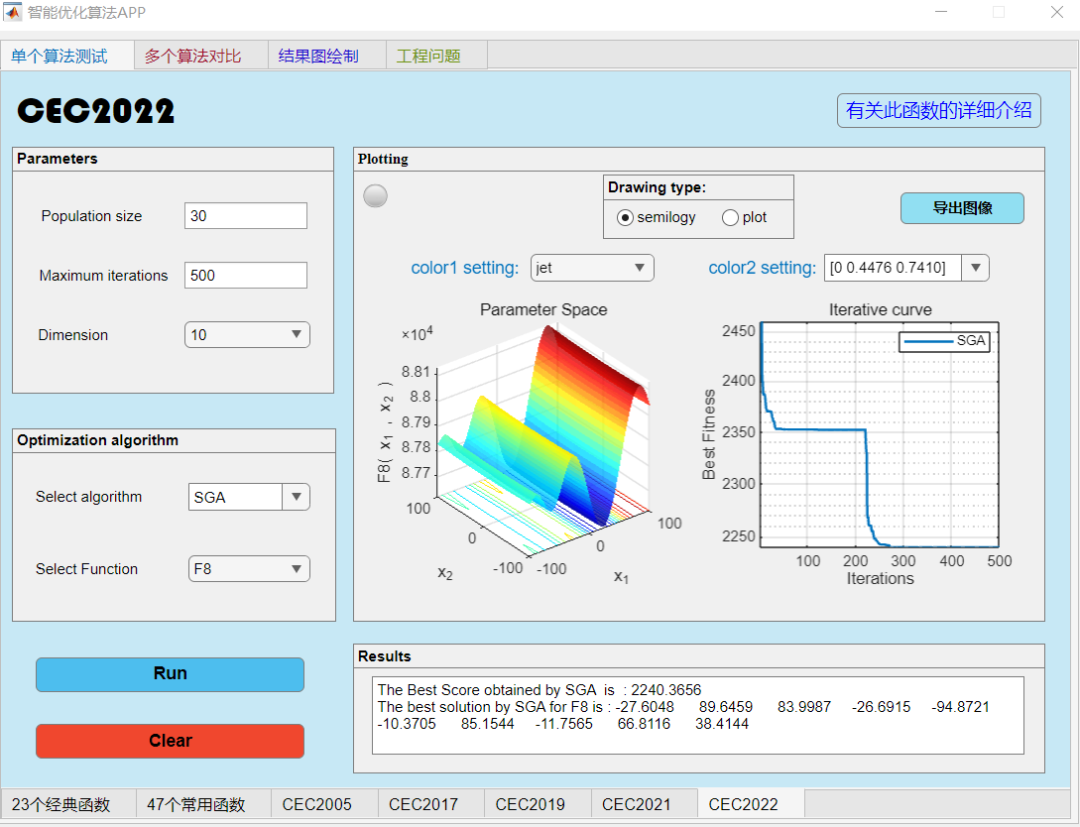
随机选个函数集，就选CEC2022函数集吧！

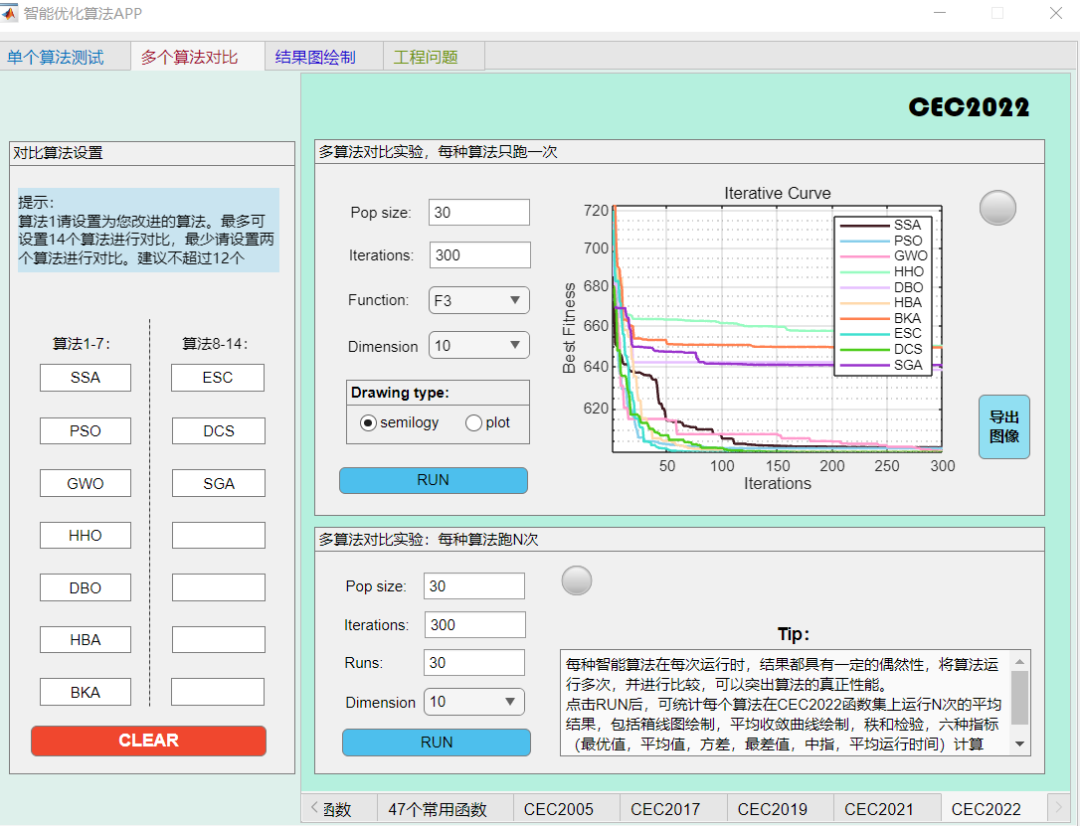
轻松与各大常见的、较新的优化算法进行对比（SSA，ESC，PSO，DCS，GWO，HHO，DBO，HBA，BKA），其中SGA就是本文的算法啦。

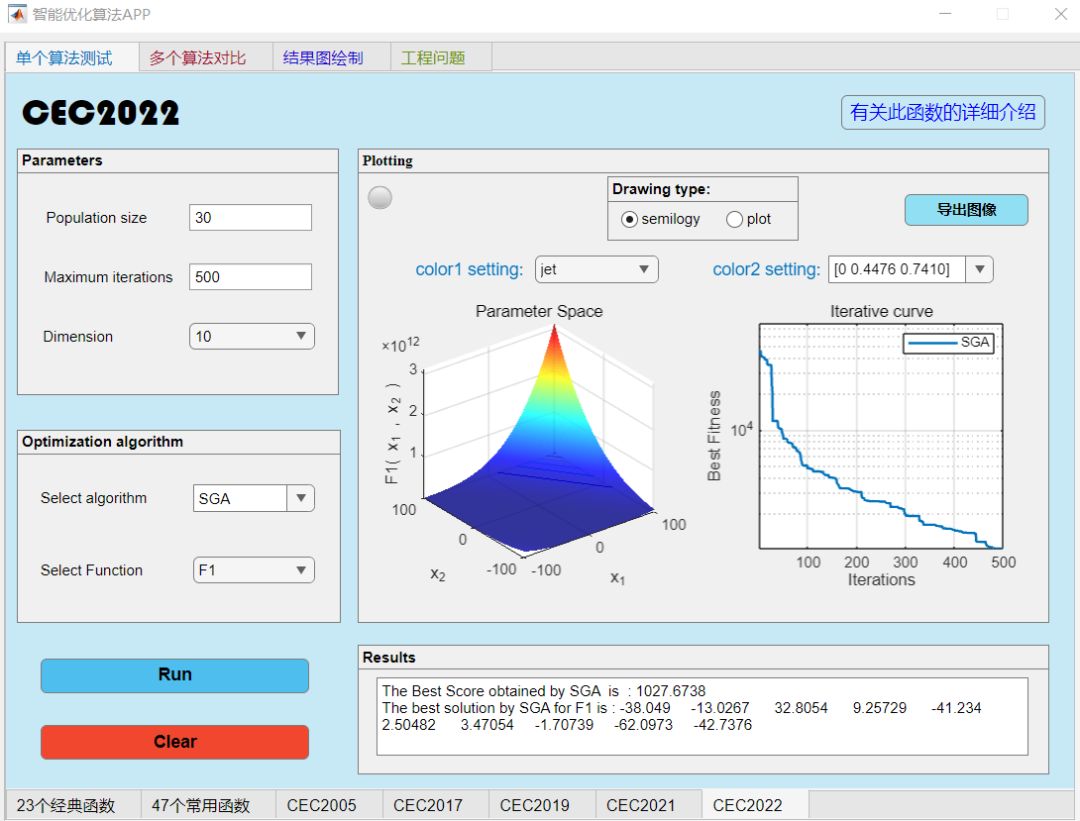
F1函数：

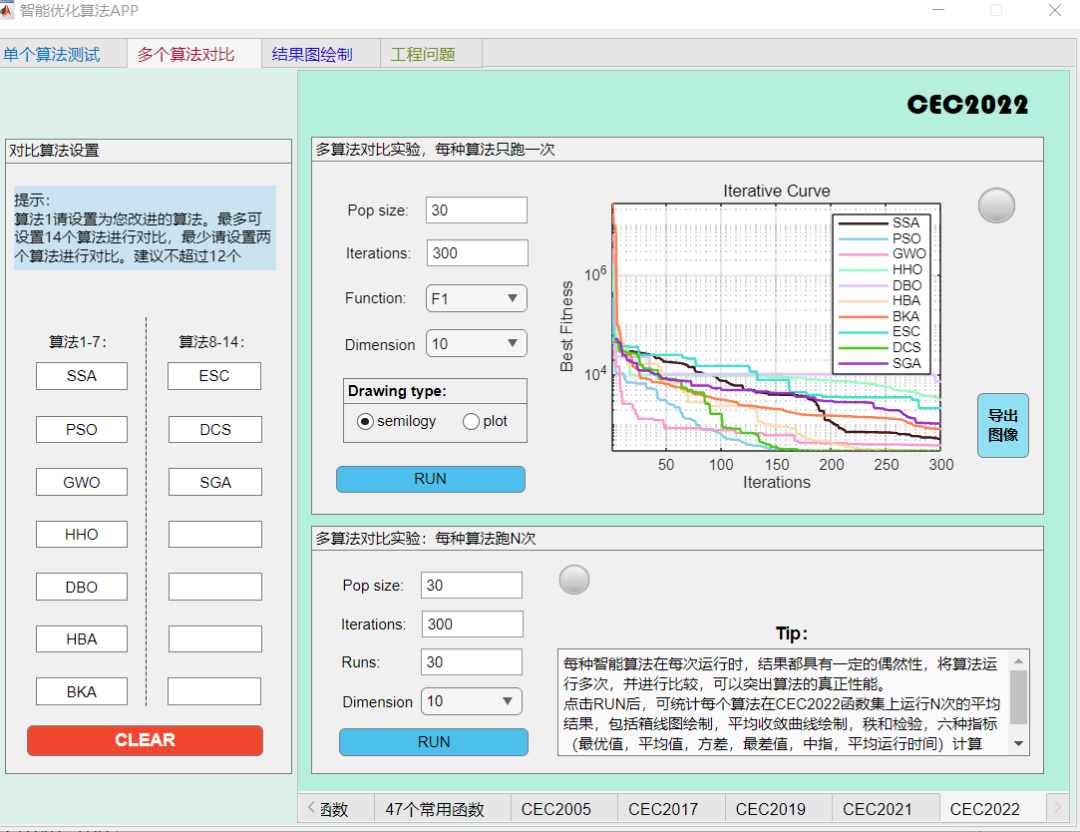
F2函数：

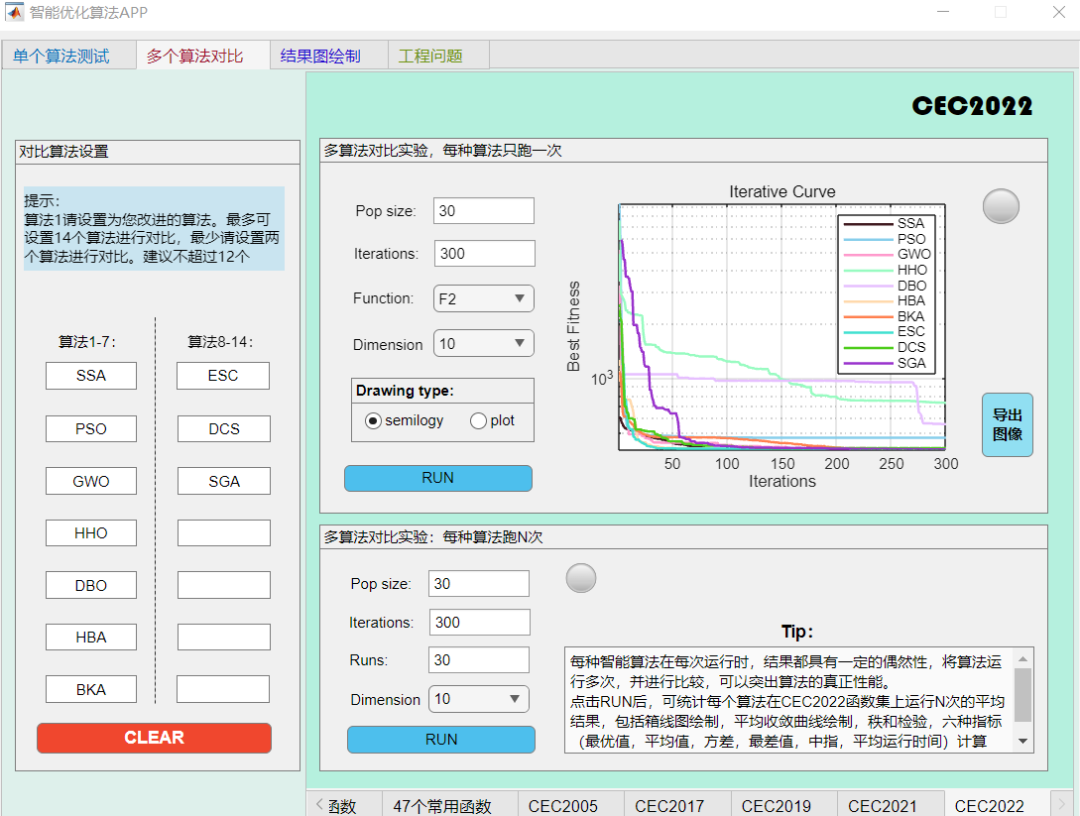
F3函数:

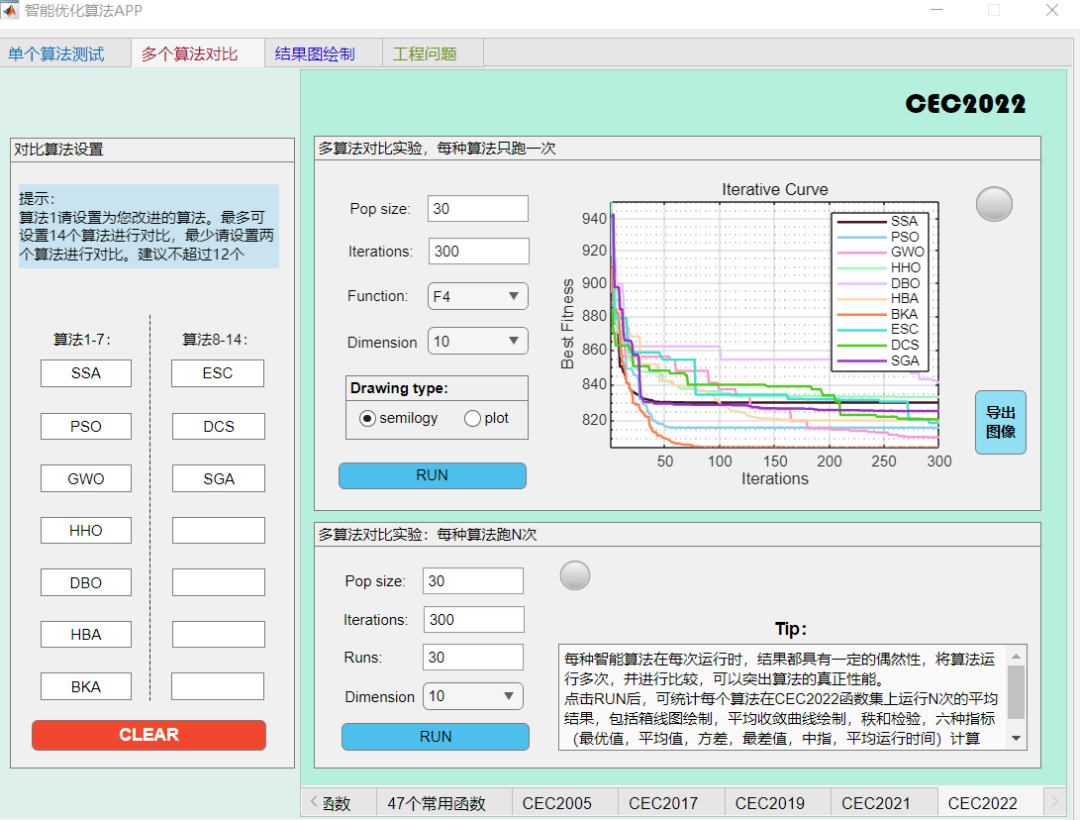
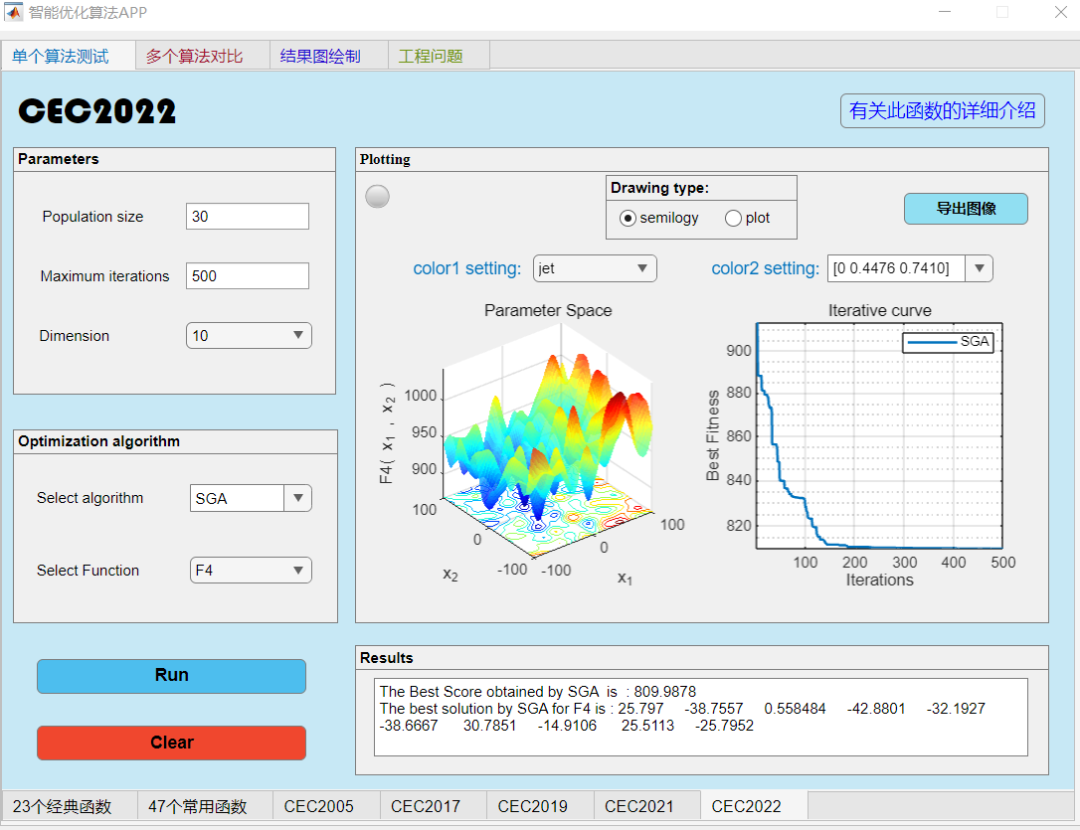
F4函数:

单个函数测试：

3.MATLAB核心代码

function [gBestScore,gBest,cg] = SGA6(Np, Max_iter, Xmin, Xmax, D, fobj)
Pos = initialization(Np,D,Xmax,Xmin);
Vel = zeros(Np,D);
gBest = zeros(1,D);
gBestScore = inf;
cg = zeros(1,Max_iter);

for i = 1:Np
    fitness(i) = fobj(Pos(i,:));
end

[gBestScore, index] = min(fitness);
gBest = Pos(index,:);

cg(1) = gBestScore;
t = 2;

while t < Max_iter
    coe = (4*(t/Max_iter))/exp(4*(t/Max_iter));
    fi = rand()*2*pi;
    for i = 1:Np
        acc = ((gBest - Pos(i,:)) - 1.29*Vel(i,:).^2*sin(fi))*10^-2;
        Vel(i,:) = coe*Vel(i,:) + acc;
    end

   [~,index] = sort(fitness);
   for i = 1: Np
       New_Pos(i,:) = Pos(index(i),:);
       New_Vel(i,:) = Vel(index(i),:);
   end
   Pos = New_Pos;
   Vel = New_Vel;
    a = 4*rand() - 2;
    b = 3*rand() -1.5;
    c = 2*rand() - 1;

    for i =1:Np
        aa(i,:) = Pos(i,:)*fitness(i);
        bb(i) = Np*fitness(i);
    end
    Xc = sum(aa)/sum(bb);
    Pos = Pos + Vel;
    iffi < pi
            for i = 1:Np
                if i<=1/5*Np
                    Pos(i,:) = Pos(i,:)  + a*(gBest - Pos(i,:)) + Vel(i,:);    
                elseif  1/5*Np< i && i < 4/5*Np
                    Pos(i,:) = Pos(i,:)  + a*(gBest - Pos(i,:)) + b*(Xc -Pos(i,:)) - c*(Pos(Np,:) + Pos(i,:))  + Vel(i,:);  
                else
                    Pos(i,:) = Pos(i,:)  + a*(gBest - Pos(i,:)) + b*(Xc -Pos(i,:)) + Vel(i,:);  
                end
                Flag4ub=Pos(i,:)>Xmax;
                Flag4lb=Pos(i,:)<Xmin;
                Pos(i,:)=(Pos(i,:).*(~(Flag4ub+Flag4lb)))+Xmax.*Flag4ub+Xmin.*Flag4lb;
            end
    else
        if rand>0.5
            for i = 1:Np
                Pos(i,:) = Pos(i,:) + (Pos(i,:) - gBest)*rand;
                Flag4ub=Pos(i,:)>Xmax;
                Flag4lb=Pos(i,:)<Xmin;
                Pos(i,:)=(Pos(i,:).*(~(Flag4ub+Flag4lb)))+Xmax.*Flag4ub+Xmin.*Flag4lb;
            end
        else
            for i = 1:Np
                Pos(i,:) = gBest + (Pos(i,:) - gBest).*rand.*Brownian(D);
                Flag4ub=Pos(i,:)>Xmax;
                Flag4lb=Pos(i,:)<Xmin;
                Pos(i,:)=(Pos(i,:).*(~(Flag4ub+Flag4lb)))+Xmax.*Flag4ub+Xmin.*Flag4lb;
            end
        end
    end        

    for i = 1:Np
        fitness(i) = fobj(Pos(i,:));
    end
    for i=1:Np
        if gBestScore > fitness(i)
            gBest = Pos(i,:);
            gBestScore = fitness(i);
        end
    end
    t = t +1;
    cg (t) = gBestScore;
end
end

function o = Brownian(D)
    T = 1;
    r = T/D;
    dw = sqrt(r)*randn(1,D);
    o = cumsum(dw);
end

4.参考文献

Tian A Q, Liu F F, Lv H X. Snow Geese Algorithm: A novel migration-inspired meta-heuristic algorithm for constrained engineering optimization problems[J]. Applied Mathematical Modelling, 2024, 126: 327-347.

完整代码获取

后台回复关键词：

TGDM839

获取更多代码：

或者复制链接跳转：https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu