融合黑寡妇思想的蜣螂优化算法，代码复现，带消融实验，MATLAB代码

本期文章复现一篇发表于2024年5月8号的一篇改进蜣螂算法。

论文引用如下：

[1]孔令崧,石颉,孙浩,等.融合黑寡妇思想的蜣螂优化算法[J/OL].微电子学与计算机,1-15[2024-05-09].

改进的蜣螂优化算法原理如下：

改进策略

改进点1： ICMIC混沌映射策略在种群初始化的应用

种群初始化在DBO中随机生成，会导致种群初始化分布不均匀，将ICMIC混沌映射策略应用于蜣螂种群初始化，可以提高种群多样性。

ICMIC混沌映射公式如下：

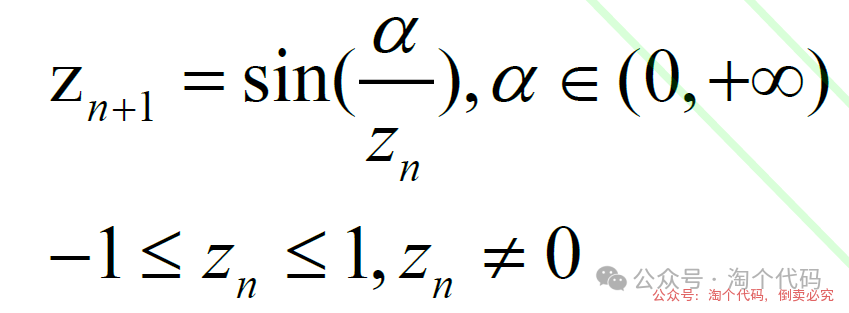
改进点2： 融合黑寡妇算法思想于滚球蜣螂阶段

在基本的蜣螂算法中，由于产卵蜣螂、小蜣螂、偷盗蜣螂位置更新的上下界会受到最佳位置的影响，且上界会随迭代次数的增加逐渐变小，而下界逐渐变大，使得三种蜣螂位置变化的范围逐渐缩小，主要起到了局部开发的作用。因此蜣螂算法的全局搜索主要通过滚球蜣螂的滚球、跳舞行为实现。然而蜣螂算法在滚球行为中只依赖于全局最差值，缺乏与其他种群个体的联系，从而易导致全局搜索能力低下，且该做法存在收敛速度慢、需更多迭代次数的问题。对此文章提出使用黑寡妇算法替换滚球行为算法。黑寡妇算法将黑寡妇蜘蛛在蛛网中的运动模型转化为线性和螺旋两种形式，位置更新公式如下：

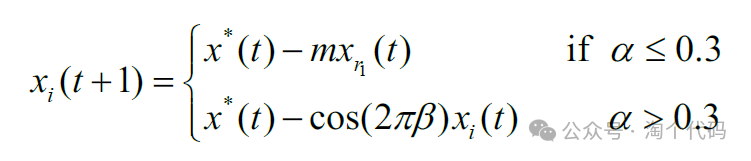
其中， x* 为全优位置， m 为0.4 到0.9 之间的随机浮点数，β为-1 到1 之间的随机浮点数，xr1 为种群中的其他个体。

信息素(pheromone)是黑寡妇种群的另一个特质，在交配的过程中起到了重要的作用。强壮成熟的雌蛛散发的信息素浓郁，暗示自身个体为繁殖力强盛的对象。因此雄蛛仅凭信息素就能选择合适对象，降低繁殖成本，而信息素过低的雌蛛将被种群淘汰，黑寡妇算法将信息素定义为：

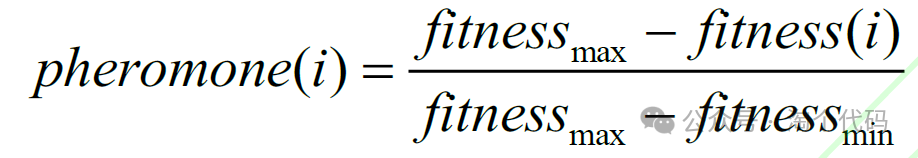
其中，fitnessmax 为全局最优个体的适应度，即全局最优值，fitnessmin 为全局最差个体的适应度，即全局最差值，fitness(i) 为当前个体适应度。

当信息素过小时，个体将会被新个体替代，位置更新公式为：

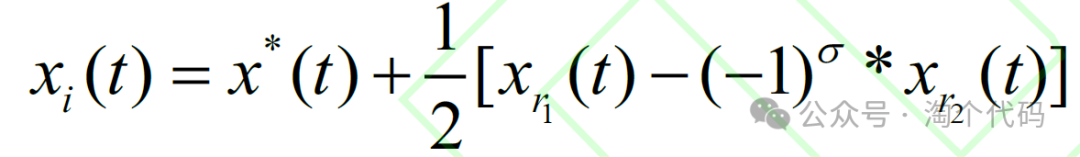
其中，xr1 与xr2 为种群中的两个不同个体。

改进点3： 自适应T 分布改进因子

在基本蜣螂算法迭代的后期，各蜣螂个体将快速同化，蜣螂种群迅速聚集到当前的最优位置附近，若当前并非全局最优位置，则针对当前最优位置附近的搜索的效果会大打折扣，浪费了搜素资源，从而导致错过最佳位置。针对该问题，常使用变异扰动操作对个体进行干扰，从而避免局部最优。对于蜣螂算法，小蜣螂觅食行为直接涉及全局最优位置，文章采用以迭代次数自由度参数的t 分布变异扰动因子，对小蜣螂觅食行为进行扰动。

t 分布即是学生分布，决策参数为自由度参数m，其概率密度函数为：

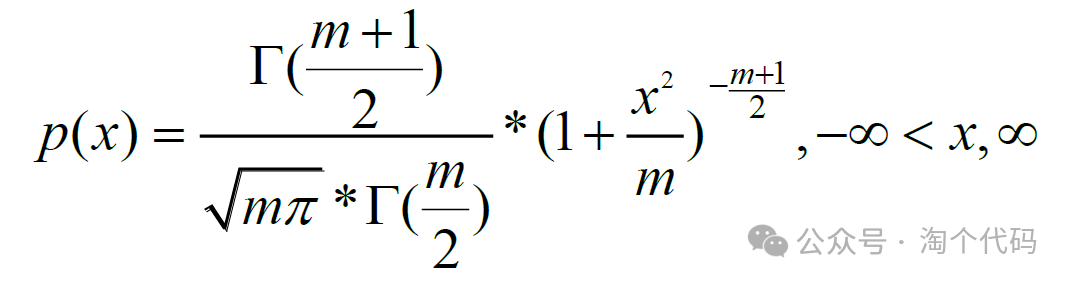
自适应t 分布变异扰动因子具有柯西、高斯分布两种特性，使得蜣螂算法在迭代前期具有较好的全局开发能力，在迭代后期具有良好的局部探索能力，并提高算法的收敛速度。具体的位置更新方式如下：

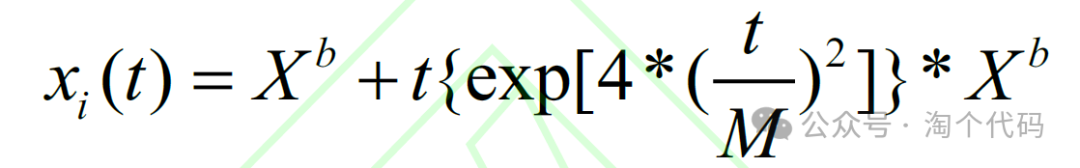
其中， t 表示了t 分布下的随机数。

结果展示

在CEC2005函数集进行测试，并与减法优化器(SABO)，鲸鱼算法(WOA),哈里斯鹰算法(HHO)，北方苍鹰算法(NGO)，灰狼算法(GWO)，原始蜣螂算法(DBO)进行比较。

在CEC2005中测试：

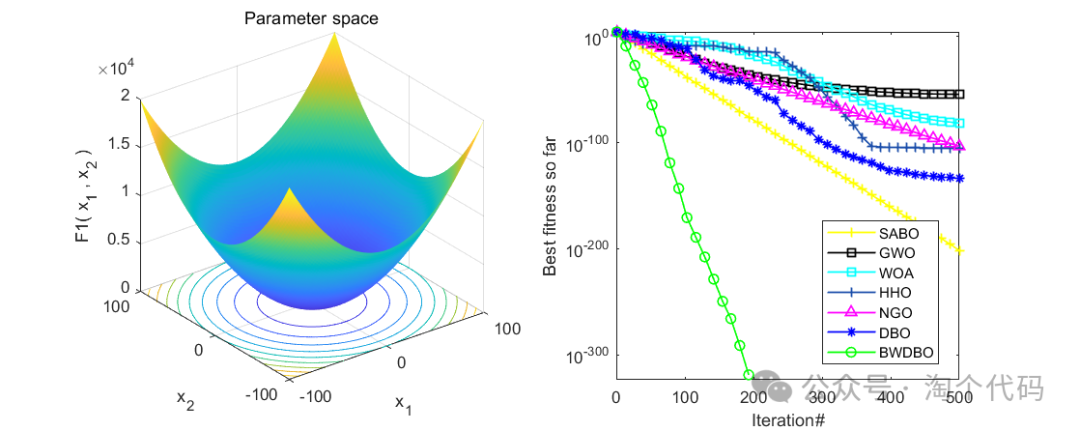
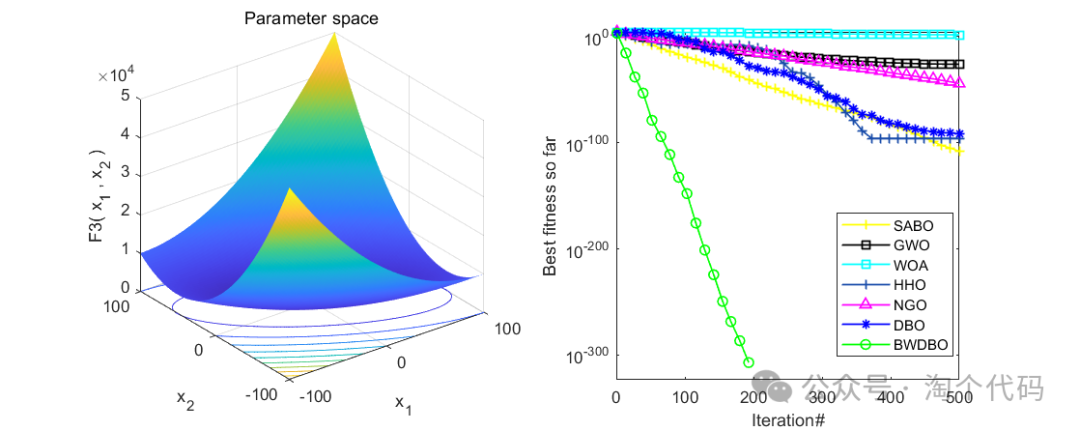
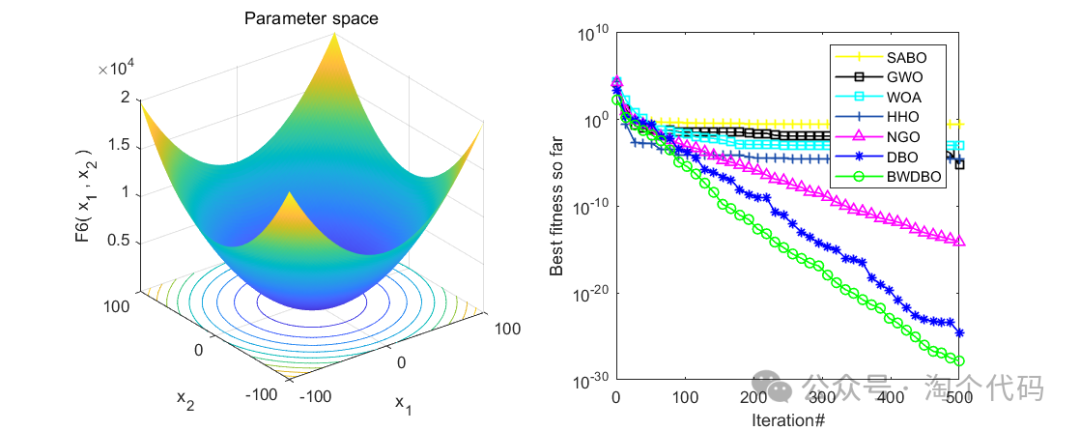
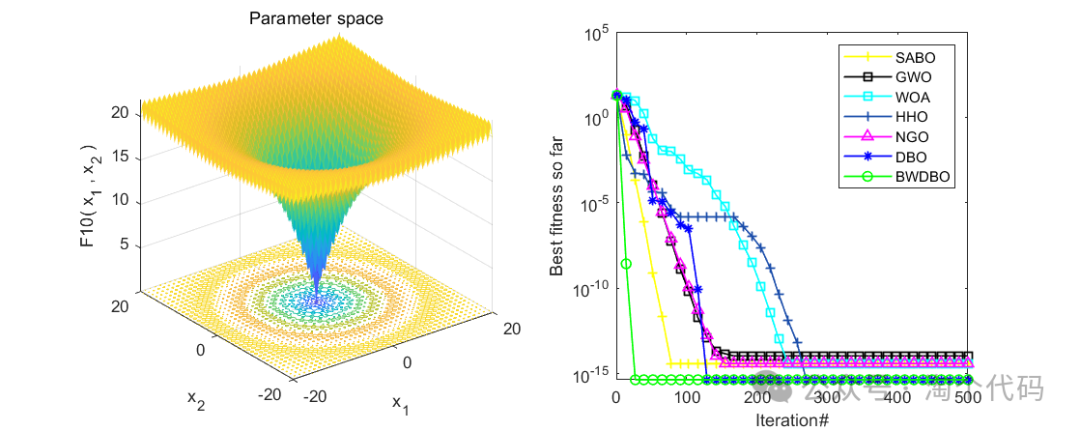
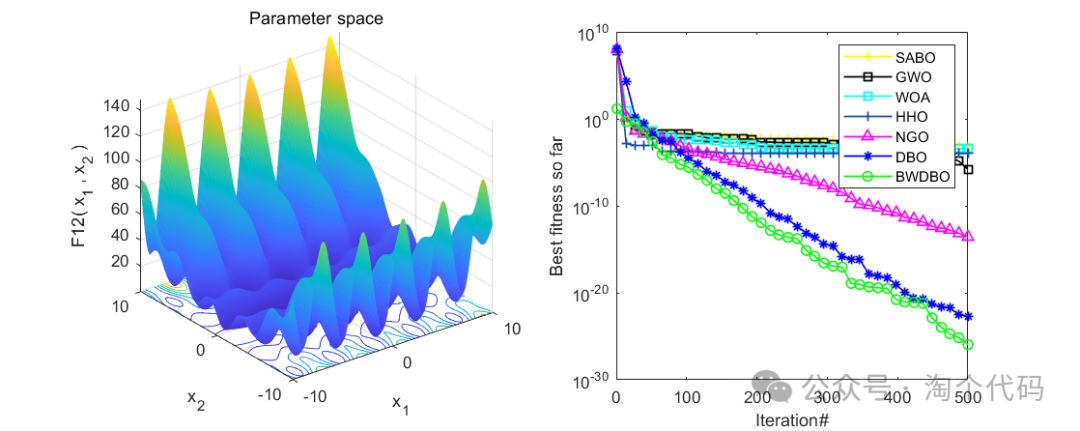
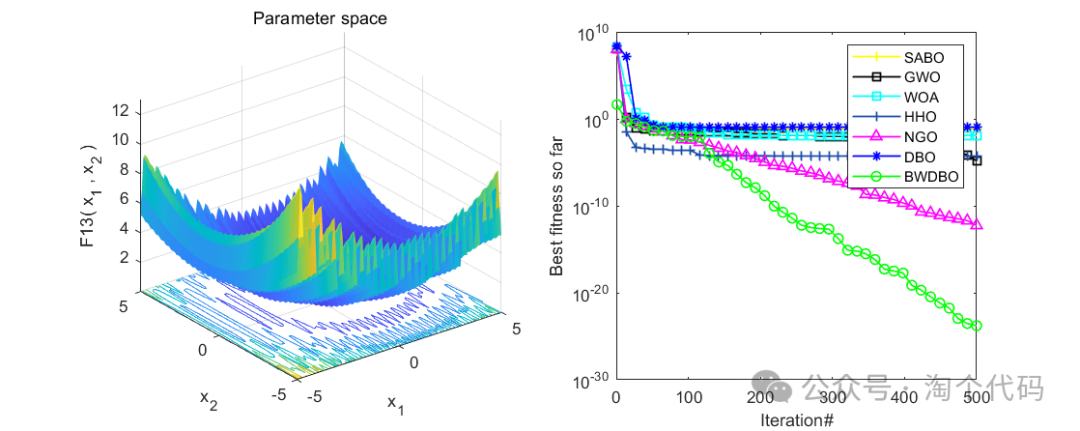
消融实验展示

为了验证文章提出的不同改进策略的有效性，将DBO与前述三种策略结合得到以下三种算法：

1) DBO 加入混沌映射后得到DBO1;

2) 使用黑寡妇替换滚球蜣螂滚球行为后得到DBO2;

3) DBO 加入自适应分布改进因子后得到DBO3；

同时将三种改进策略两两结合得到DBO1+2 、DBO1+3。结果如下：

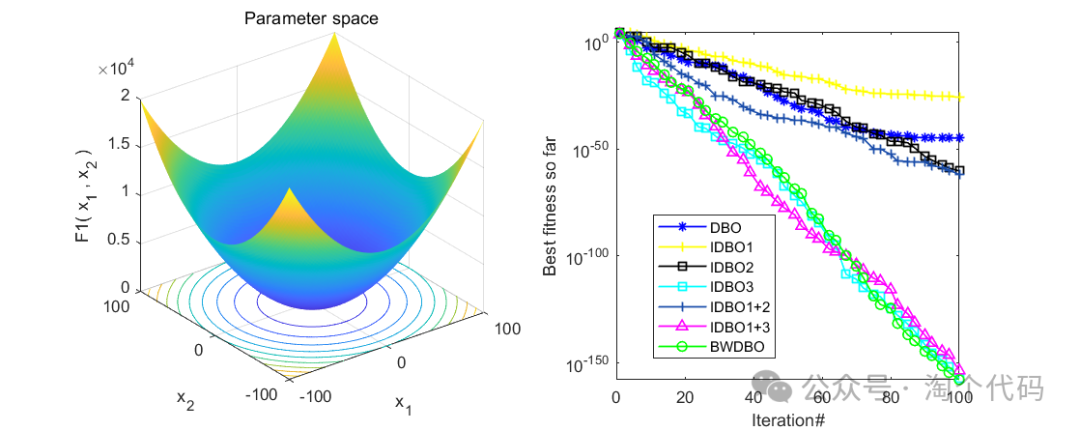
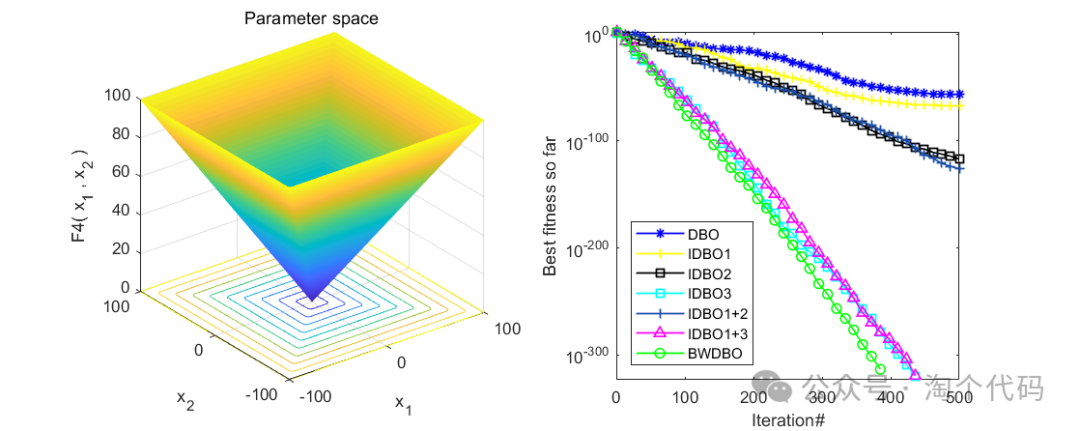
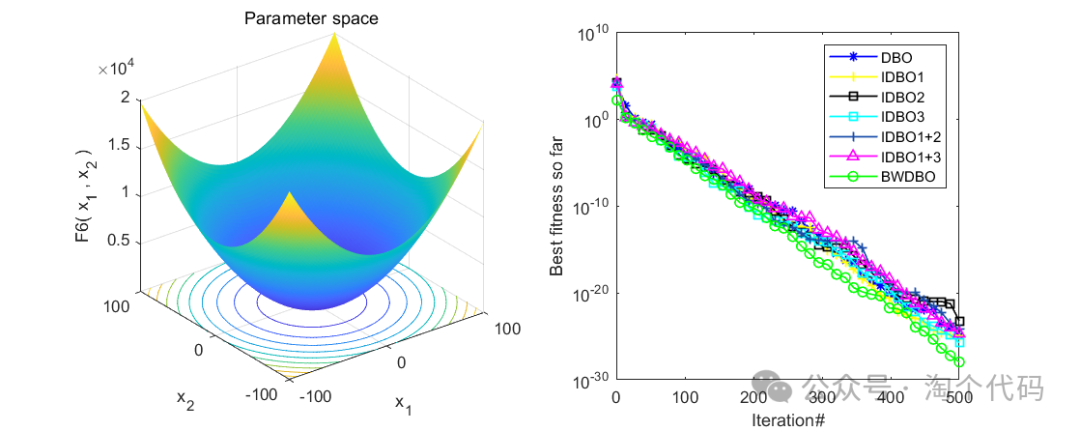
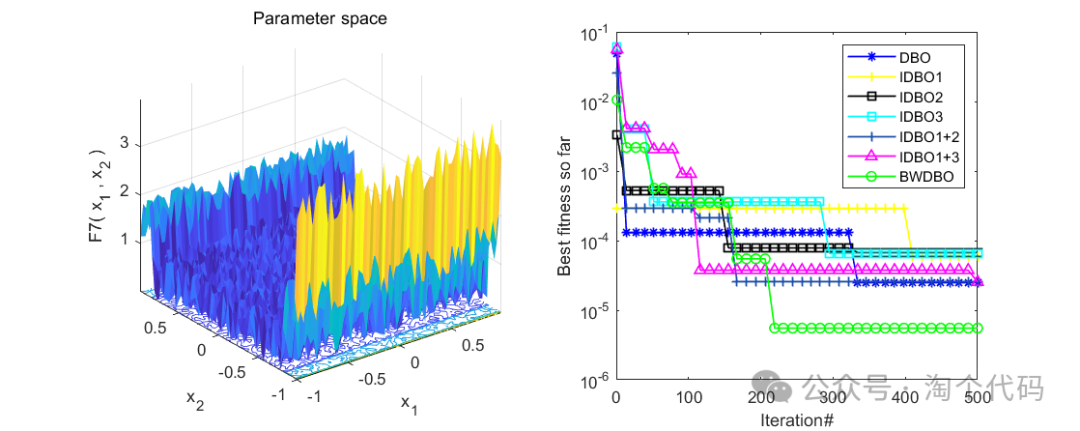
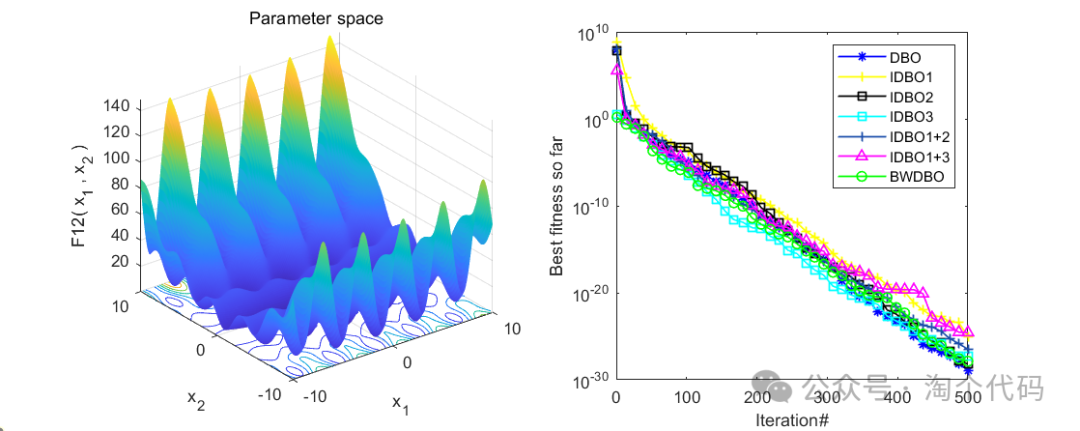
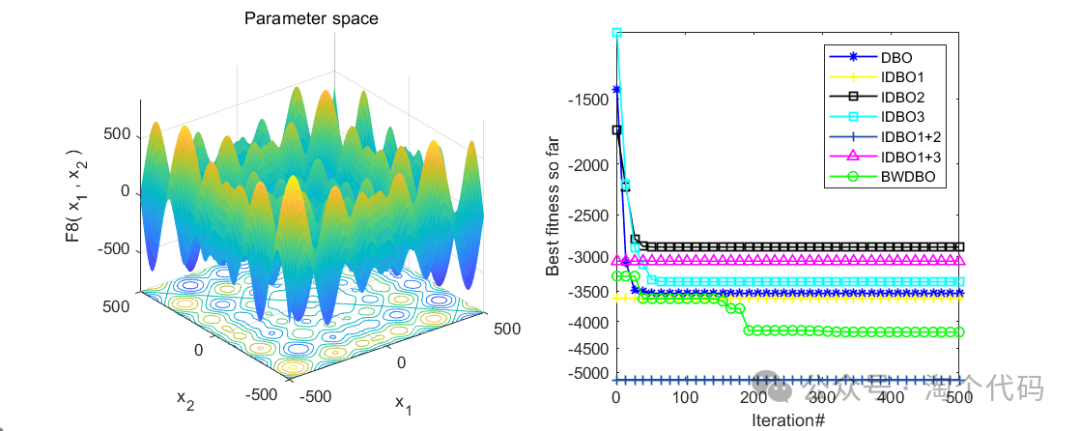
整体来看，效果还是很不错的，每个策略都起到了相应的效果

代码目录

本期代码获取链接：

融合黑寡妇思想的蜣螂优化算法：
https://mbd.pub/o/bread/mbd-ZpWalJ1u

已将本文代码添加至蜣螂优化算法全家桶。

蜣螂优化全家桶目前包含内容如下：

多策略改进蜣螂优化--螺旋搜索+最优值引导+反向学习策略（原创）

改进蜣螂优化--采用莱维飞行和三角形游走策略（原创）

独家原创！随机游走与纵横交叉的蜣螂优化算法（原创）

融合鱼鹰与自适应t分布的蜣螂优化算法(OTDBO)（原创）

改进正弦算法引导的蜣螂优化算法(MSADBO)（文献复现）

融合麻雀追随机制扰动与柯西变异的蜣螂优化算法，历史位置图，平均适应度收敛图一次性全部搞定，MATLAB代码（文献复现）

中科院一区论文复现，改进蜣螂算法，Fuch映射+反向学习+自适应步长+随机差分变异，MATLAB代码（文献复现）

以上代码分为MATLAB、Python代码版本

全家桶链接：

蜣螂算法全家桶Matlab代码链接：


https://mbd.pub/o/bread/mbd-ZZmVl5hv


蜣螂算法全家桶Python代码链接：


https://mbd.pub/o/bread/mbd-ZZuYmpts