SCI一区同核分子优化算法，原理详解，MATLAB代码免费获取

原创已于 2025-05-28 15:23:59 修改 · 907 阅读

CC 4.0 BY-SA版权

文章标签：

于 2024-11-29 08:40:13 首次发布

同核分子优化(Homonuclear Molecules Optimization，HMO)是一种用于优化复杂和非线性问题的群智能算法。根据玻尔原子模型和同核分子的结构，HMO的灵感来自于原子周围电子的排列。该算法基于在给定量子数的搜索空间中创建一组原子的初始种群以及与每个原子(搜索代理)相关联的电子。在每次迭代中，选择每个原子的最佳电子作为原子核的新位置，多个原子向具有最佳溶液的原子移动，形成同核分子。

该成果于2022年发表在计算机科学领域1区SCI期刊“Knowledge-Based Systems”上，目前被引20次。

1、算法原理

（1）原子的电子排列

原子由质子、中子和电子组成。玻尔提出了氢原子的量子模型。根据这个模型，原子核周围的电子在一定的电路中运动，每个电子都有一定的能量。这些能量值中的每一个都被称为能级或能量层，并用n(1,2,3,4，…)的值来指定。玻尔原子模型表明，原子半径随n2的增大而增大。

其中e为基本电荷，m0为电子质量，ε0为自由空间介电常数，h为普朗克常数，π为常系数(圆的周长与直径之比)。

下图显示了基于玻尔原子模型的原子核周围电子云的示意图。

电子是分层分布的。每一层由一个或两个子层组成，每个子层有一个或几个轨道。每个原子的电子由四个量子数指定，对应于它的主层、子层、轨道和自旋。主量子数表示电子所属的层，在该层中找到电子的可能性很大。这个数字用n表示，是一个整数。

子层数等于主量子数。每一子层有一个角动量量子数l和一个0 ~ n-1的整数，用以下字母表示:

每个子层由一定数量的轨道组成，由下式计算:

每个子层的轨道由磁量子数(ml)确定，并由1，−1和0之间的整数组成。每个轨道充满两个电子，它们具有不同的电子自旋量子数。例如，这个元素的36个电子围绕原子核的排列是。

（2）HMO算法建模

在HMO算法中，电子负责寻找期望问题的解。考虑到电子的速度非常高且接近光速，在HMO算法中，考虑到最大可能距离，电子作为搜索代理随机分布在原子核周围。

选择具有最佳解的原子的每个电子作为互易原子的原子核的新位置，并重复此过程，直到原子核接近解(探索阶段)。该算法被设计成能够对具有多个局部极值的问题找到多个解的方式。为了使算法能够高精度地找到问题的解，与大多数其他基于群的算法类似，原子必须向具有最佳解的原子移动，最终导致同核分子的形成。

为了进一步描述所提出的HMO算法的性能，将优化过程分为以下五个阶段，如下图所示。

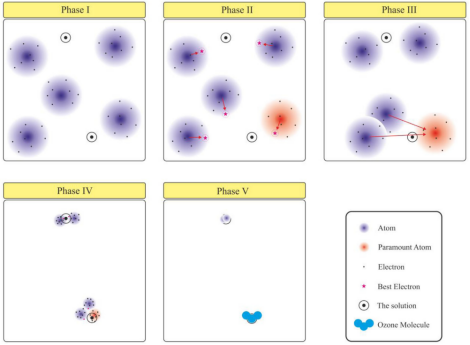
第一阶段：初始阶段在这个阶段中，随机产生由几个原子序数为z的原子（N）组成的初始布居，以在搜索空间中形成由m个原子组成的同源分子。换句话说，根据问题的维度和类型选择初始参数的数量是用户的责任。选择建议值时，应考虑以下因素：

1.对于高维和多个局部极值的问题，使用较重的原子。

2.如果不需要找到局部解，则可以在搜索空间中考虑更少的原子。

3.如果目标是找到局部极值，并且精确解不是很重要，则可以使用具有少量原子的分子。

4.建议所选原子的原子序数（z）大于问题维数（D）。在此基础上，可以这样写：

在搜索空间中放置原子之后，电子随机分布在原子周围。具有最佳解的原子被选为最重要的原子。原子核周围的电子云的排列是基于电子到原子核的距离。因此，使用主量子数（n）。在原子i的算法开始时，这些距离基于以下等式计算：

其中，Rj i是指原子i的层j的电子到原子核的最大可能距离，α1是指与方程1相关的玻尔半径。其值应基于问题的搜索空间来考虑。在本研究中，提出了以下公式来计算α。

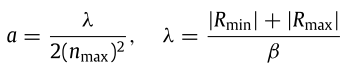
在该等式中，Rmax是指搜索空间沿沿着轴的最大边界，Rmin是指搜索域沿沿着轴的最小边界，nmax是指与期望元素相关的最大量子数，β是距离控制系数。如果电子福尔斯落在搜索域的边界之外，则它将被定位在边界的边缘。下图展示出了假设β = 2时原子围绕边界的运动。

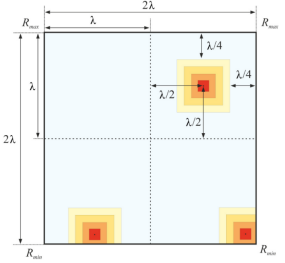
电子的排列可以基于周期表的元素或假设的元素来完成。在每次迭代中，使用以下等式计算电子的位置：

其中Xelectront i是指原子i在迭代t中的电子位置，Xnucleust i是指原子i在迭代t中的原子核位置，ri j是区间[−R j i，R j i]中的随机向量。在算法性能的示意图中，五个氧原子（z = 8）分布在搜索空间中，形成一个臭氧分子（O3）作为全局极值的位置。在该图中，还假设搜索空间有两个相似的最优解。

第二阶段：探索阶段在第二阶段，根据原子的位置和分布的电子，计算所有电子的适应度值，同时确定每个原子的代价函数和最佳电子。使用成本函数，为每个原子Xelectronbest i指定具有最佳解的电子，并且使用以下等式计算每个原子的核的新位置：

其中t表示迭代步长。最后，更新最重要原子的位置。在新的迭代中，如果另一个原子提供了比所选择的首要原子更好的解，则它们的位置将被切换。

第三阶段：为了使算法能够找到问题的精确解并确定局部极值，一些原子应该向最重要的原子移动，以形成一个同质分子。因此，通过考虑一个分子及其原子的数量，几个原子可以向最重要的原子移动。在该算法中，几何上离最高原子较近的原子将向最高原子移动，因此，使用欧几里德距离来确定相邻原子。

其中dti等于最重要原子的核与第i个原子的核的位置之间的欧几里得距离（Xnucleust_i），并且Xnucleus_parallett表示迭代t时最重要原子的核的位置。在这个假设下，m-1个相邻原子将能够通过最重要的原子来增加它们的学习，并且通过接近更好的原子来建立算法的利用性质。

m−1个相邻原子形成均质分子的运动如下：

其中γ是距离缩减因子，并且是0和1之间的随机向量。

最小量的γ增加了运动中原子的最佳电子的效应，降低了均质分子的效应。在本研究中，γ介于0和0.1之间。

第四阶段：迭代和收缩阶段在此阶段，重复第II和第III阶段的计算过程，以获得最佳解决方案。为了更快的收敛以及找到一个更精确的解决方案的问题，它建议在每次迭代中减少的电子云周围的核的大小，当且仅当最好的电子位于第一层。这个过程是另一种类型的开发属性，被认为是所有原子。在本研究中，以下函数用于原子半径的收缩：

其中Maxt是指最大迭代次数（epoch），t是指当前迭代步长，表示原子i的层j中电子的最大可能距离的新值。

第五阶段：第五阶段（终止阶段）是算法的最后一步，其中确定算法解决方案。在这个阶段，当求解过程达到最终历元数（t = Maxt）或目标函数Efinal的最终误差小于收敛速率（例如）时，计算结束，解收敛。

在本研究中，检验函数的值即为误差。在这种情况下，最重要原子的集合和它们在开采期间彼此相邻的相邻原子组成同核分子。最后，将组成分子的最高原子核的位置作为全局最优解。值得注意的是，其他原子的位置决定了其他局部最优解。HMO算法的流程图分为五个阶段，如下图所示。

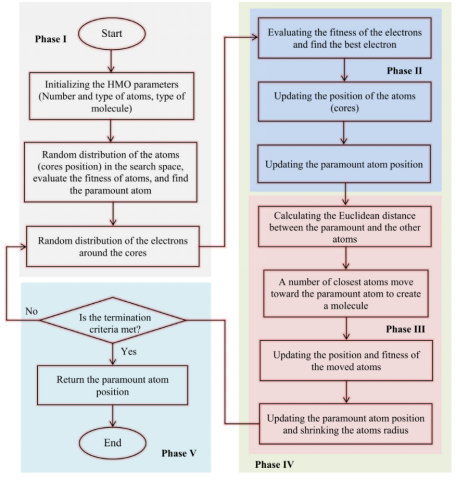
2、结果展示

本期代码执行效率不是很高，就不建议加入优化算法APP啦，只是做一个简单分享。代码结果如下：

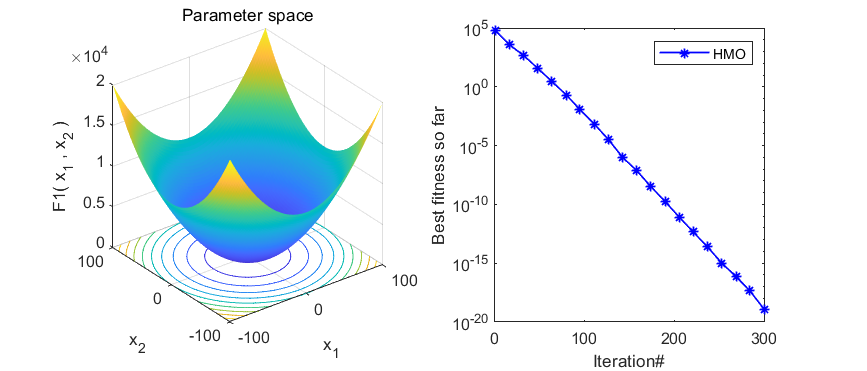
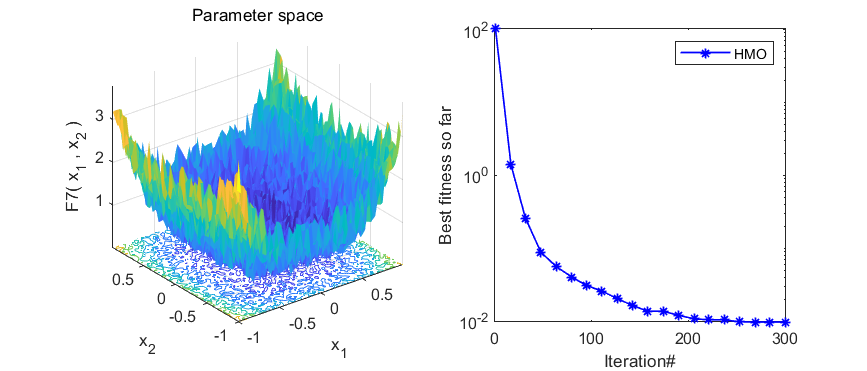
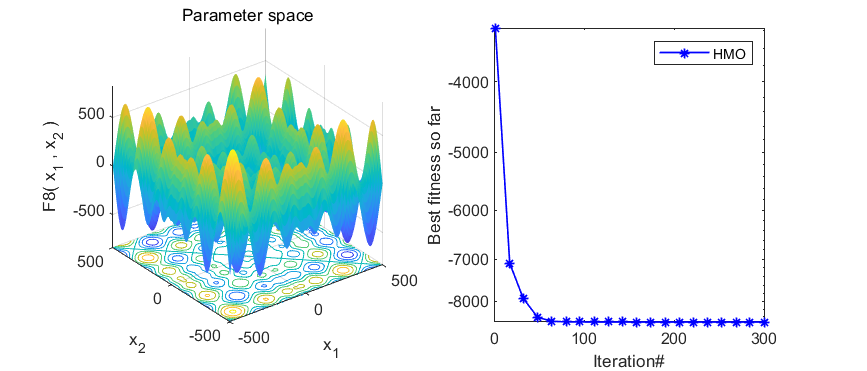
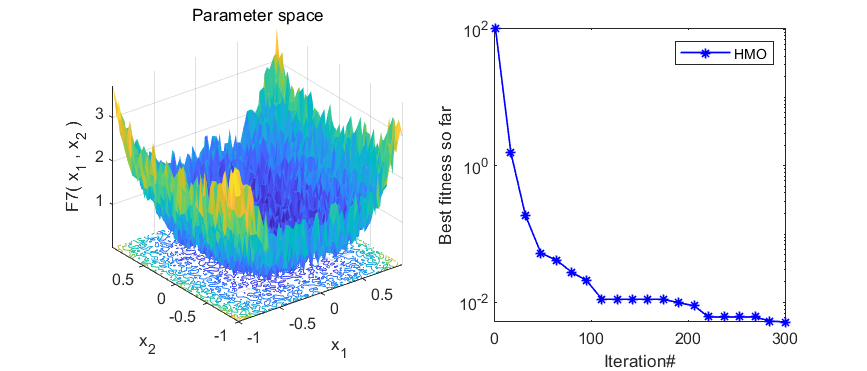
3、MATLAB核心代码

function [Best_pos,Best_fitness,Convergence_Rate] =  HMO(N,MaxIt,Min,Max,D,Function)
Size=[1 D];
%% HMO Parameters
Atomic_number = 34;    % The Number of Electrons , Maximum 118  
N_Homonuclear = 8;     % The Number of Atoms of Homonuclear Molecule
Beta=2;                % See (Eq. 7)


%% Initialization
Layer = Electron_arrangement(Atomic_number );  % This function determines the type of element See (Eq.2 ,Eq.3, and Eq.4)
N_Layers = size(Layer,1);


% Calculating  the parameters related to Bohr radius
Landa = (abs(Min)+abs(Max))/Beta;    % See (Eq. 7)
a = Landa/(2*N_Layers^2);            % See (Eq. 7)


% Initializing the position of atoms 
Atom_Paramount_Cost = inf;
for i=1:N   
 Atom(i).X = unifrnd(Min,Max,Size);


 % Calculating the fitness of electrons
 Atom(i).Cost = Function(Atom(i).X);


   if Atom(i).Cost<Atom_Paramount_Cost
     Best_Atom_X = Atom(i).X;
     Atom_Paramount_Cost = Atom(i).Cost;
     N_Best = i;    % The paramount Atom
   end


Best_Electron(i).X = Atom(i).X;
Best_Electron(i).Cost = Atom(i).Cost; 
end


% Calculating the Bohr radius
k=0;
for i=1:N
  B = N_Layers;
  L_Best_Electron(i,1) = N_Layers;  % The best electron of each atom
     for j=1:B 
        Atom(i).R(j) = a*(j^2);   % See (Eq. 6)
     end   
  Dr(i,1) = 1;  % This parameter is related to reduction of Distance 
end




%% The main Loops of HMO 


for it=1:MaxIt      % The iterations loop 
for i=1:N           % The atoms loop (number of atoms) 


% These two loops are related to the electrons
for j=1:N_Layers    % The layers loop (number of layers, depend on the type of atom)
for k=1:Layer(j,1)  % The electrons loops


   Atom(i).Layer(j).Electrons(k).X = Atom(i).X+unifrnd(-Atom(i).R(j),Atom(i).R(j),Size);  % See (Eq. 8)
   % The electrons position lmits
   Atom(i).Layer(j).Electrons(k).X = max(Atom(i).Layer(j).Electrons(k).X,Min);            
   Atom(i).Layer(j).Electrons(k).X = min(Atom(i).Layer(j).Electrons(k).X,Max);  


   % Calculating the fitness of electrons
   Atom(i).Layer(j).Electrons(k).Cost = Function(Atom(i).Layer(j).Electrons(k).X);


      % Updating the best electron of each atom
      if Atom(i).Layer(j).Electrons(k).Cost<Best_Electron(i).Cost 
         Best_Electron(i).X = Atom(i).Layer(j).Electrons(k).X;
         Best_Electron(i).Cost = Atom(i).Layer(j).Electrons(k).Cost;
         L_Best_Electron(i,1) = j;
      end
end
end


% Updating the atoms positions
 Atom(i).X = Best_Electron(i).X;  % See (Eq. 8)
 Atom(i).Cost = Best_Electron(i).Cost;
  
% Updating the paramount Atom 
  if Atom(i).Cost<Atom(N_Best).Cost
     A = Atom(N_Best).X;
     B = Atom(N_Best).Cost;
     Atom(N_Best).X = Atom(i).X;
     Atom(N_Best).Cost = Atom(i).Cost;
     Atom(i).X = A;
     Atom(i).Cost = B;
  end
  
  % Reduction of Bohr radius
  if  L_Best_Electron(i,1)==1 
      Atom(i).R = Atom(i).R.*exp(-10*Dr(i,1)/MaxIt); % See (Eq. 12)
      Dr(i,1) = Dr(i,1)+1;   
  else
    Atom(i).R = Atom(i).R;   
  end
  
end


% Calculating the Euclidean distance
for i=1:N
 delta = (Atom(N_Best).X-Atom(i).X);   % See (Eq. 10)
 d(i,1) = (sum(delta.^2))^0.5;          
end


[D_sort Nsort_D]=sort(d);    % Sorting the atoms to find which one is more close to the paramount 
Location_Best = find(Nsort_D==N_Best);   


% This lines is for cases that the cost of paramount atom and some other atoms is same
if Location_Best~=1
 Nsort_D(Location_Best)=Nsort_D(1);
 Nsort_D(1)=N_Best;    
end


% Moving some of atoms to the paramount atom to creat the homonuclear molecule
 for i=2:N_Homonuclear
 Atom(Nsort_D(i)).X = Atom(Nsort_D(i)).X ...
 +unifrnd(0,.1,Size).*(Atom(N_Best).X-Atom(Nsort_D(i)).X); % See (Eq. 11)
 
 % Calculating the fitness of electrons
 Atom(Nsort_D(i)).Cost = Function(Atom(Nsort_D(i)).X);


 % Updating the paramount Atom
  if Atom(Nsort_D(i)).Cost<Atom(Nsort_D(1)).Cost
     A = Atom(N_Best).X;
     B = Atom(N_Best).Cost;
     Atom(Nsort_D(i)).X = Atom(Nsort_D(i)).X;
     Atom(Nsort_D(i)).Cost = Atom(Nsort_D(i)).Cost;
     Atom(N_Best).X = A;
     Atom(N_Best).Cost = B;
   end
end
    Convergence_Rate(it,1) = Atom(N_Best).Cost;
    Best_fitness = Atom(N_Best).Cost;
    Best_pos = Atom(N_Best).X;
end

参考文献

[1]Mahdavi-Meymand A, Zounemat-Kermani M. Homonuclear molecules optimization (HMO) meta-heuristic algorithm[J]. Knowledge-Based Systems, 2022, 258: 110032.

完整代码获取

点击下方卡片，后台回复关键词：

TGDM823