注:该算法已按照智能优化算法APP标准格式进行整改,可直接集成到APP中,方便大家与自己的算法进行对比。
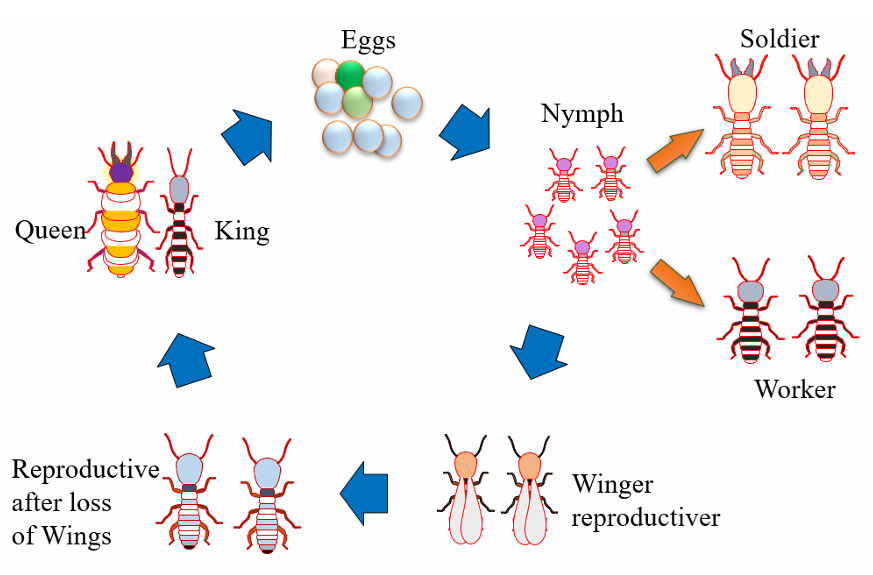
白蚁生命周期优化器(Termite life cycle optimizer,TLCO)是一种基于白蚁种群生命周期和自然界中多种动物活动策略调节的启发式优化算法。白蚁群落由三个不同的阶级组成:工蚁、兵蚁和繁殖白蚁。每个阶级都承担着一系列确保殖民地成长和生存的具体任务。
TLCO模拟了这三个阶级的活动,并在一个数学模型中实现。然后将该模型用于求解经典优化问题中的全局最优解。首先,利用工蚁、士兵和繁殖白蚁的行为来模拟勘探和开采任务之间的平衡。第二,初始种群安全地记录在每次迭代中获得的信息,并在下一次迭代中将其传输给工蚁和士兵。重复该过程,直到找到具有最小误差的全局最优值。此外,提出了一种结合Levy飞行的新函数来调节白蚁的运动,增加了白蚁的灵活性。因此,TLCO既可以在第一次迭代期间覆盖长距离以提高收敛速度,也可以在最后一次迭代期间覆盖较短距离以提高精度水平。
该成果于2023年发表在计算机科学领域1区SCI期刊“Expert Systems with Applications”上,目前被引58次。

1.原理详解
(1)随机漫步和L´evy飞行
在自然界中,动物的一些动作大多是随机的。从起点开始,动物可以向任何方向移动。例如在觅食活动中可以观察到这样的运动。在数学术语中,路径可以用一系列随机步骤表示,如以下方程所示:
其中 表示步长。人们曾多次尝试将步长转换为概率的数学公式。许多方法可以确定这些特征,但最简单的方法是众所周知的非对称和稳定L'evy分布的Mantegna算法。如果每一步 在随机漫步服从L' evy分布时,随机漫步将成为L' evy飞行。根据Mantegna算法,步长Si定义为以下方程:
其中β为L´evy分布指数,其值约束为
U和V由以下方程的正态分布得出:
其中σu和σv为以下公式给出的标准差:
在上述方程中,整数z的Gamma函数Γ表示如下:
每个步长S既可以是正值,也可以是负值。特别是,步长S*可以用长或短的距离来实现,这取决于参数β,如下图所示。基于这一特征,它是一种鲁棒的方法,适用于大搜索空间的探索和在该空间的最优解附近的开发。这些特征可以为了解元启发式算法的行为方式和原因提供一些提示和见解。
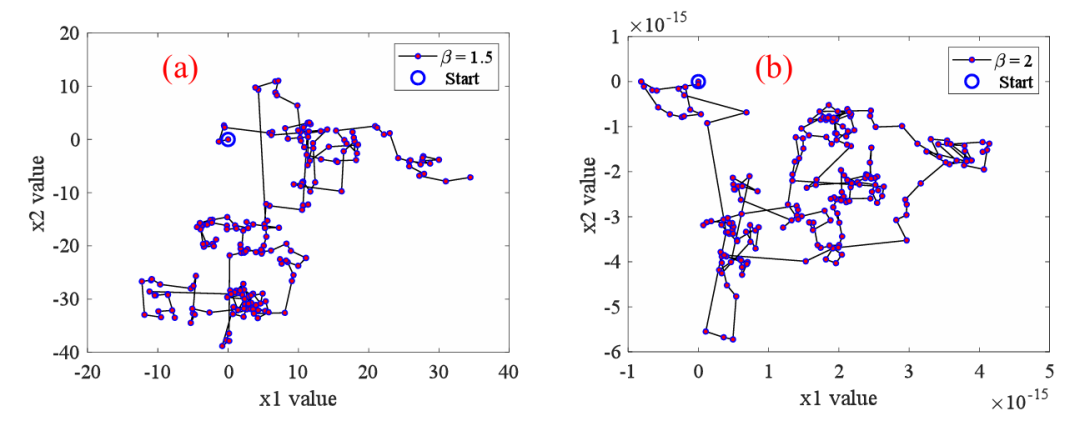
(2)白蚁生命周期优化算法中步长的改进
原始随机游动中的步长S由参数β控制,参数β的值在1到2之间。上图展示了大步长由小参数值β决定,反之亦然。对于大的参数值β,建立短的步长。一个成功的优化算法是达到两个条件:(i)快速收敛速度和(ii)高精度水平。这些条件需要足够长的移动以在第一次迭代期间快进最佳解,并且需要足够短的移动以避免局部最优问题并在最后一次迭代期间提高精度水平。在TLCO中,这可以通过在每次迭代时调整参数β的值来实现。因此,β的值在迭代过程中向上移动,以提高收敛速度和精度水平。为了在最初的几次迭代中限制搜索空间,将β值的边界条件从范围[1,2]改变为范围[1.5,2]以提高收敛速度。因此,修改步长在以下公式中呈现。
其中k是当前迭代,Kmax是最大迭代次数。
下图显示了每次迭代时β值对步长的影响。
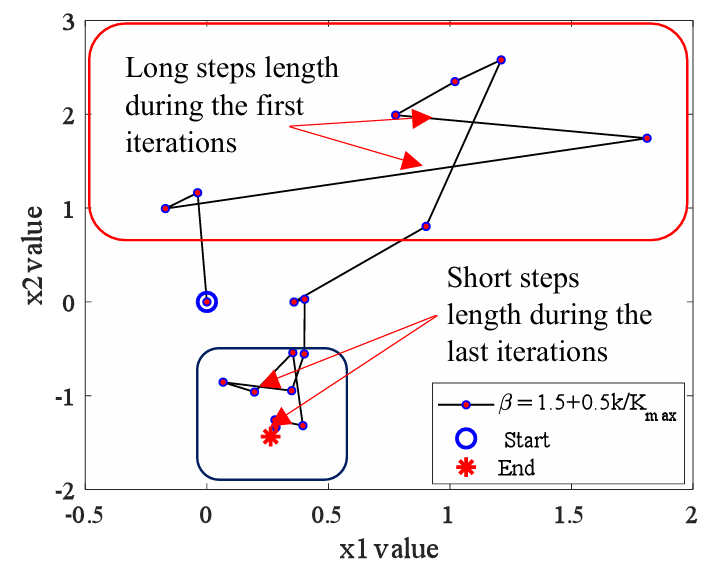
(3)白蚁生命周期优化器的通用运动策略
假设具有高质量搜索空间符号化X*→的位置是已知的。在2D中,从当前位置Xold→ 到新位置Xnew→的移动策略在下式中给出:
其中w1、w2、w3和w4是正标量向量或具有随机分布的标量数,其考虑每个单独向量的取向对新位置Xnew→的影响。
假设每个矢量w2、w2、w3、w4是其值在范围[0,1]内并且具有维度D = 2的标量矢量在下图中以第一次迭代示出:
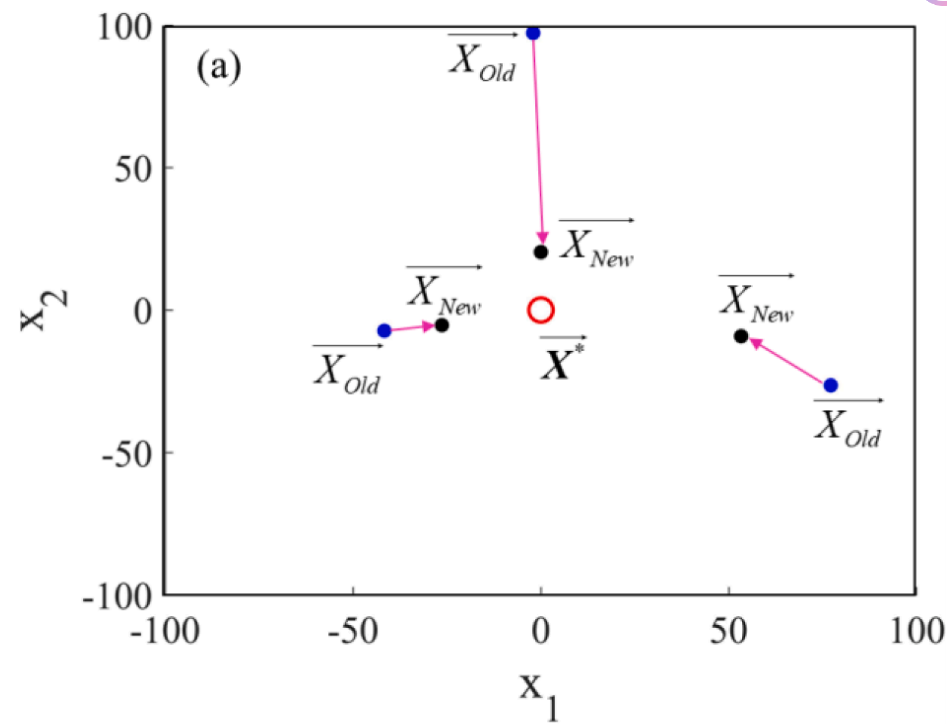
此外,如果增加迭代次数将达到收敛到X*n→的值,如图b所示。
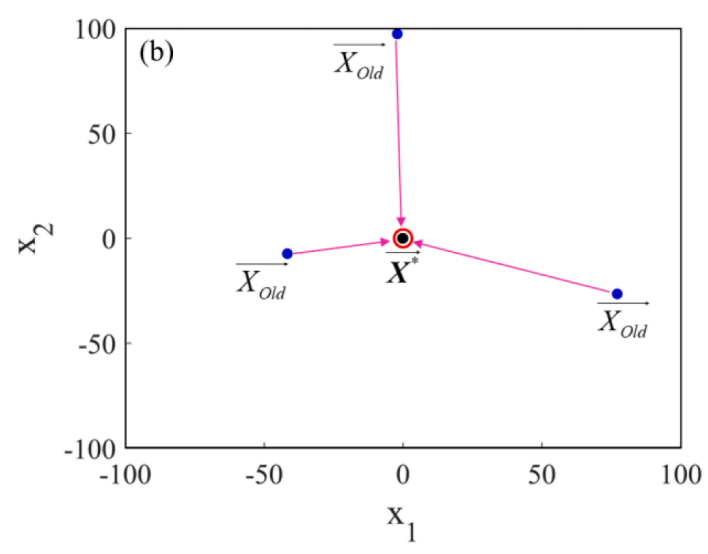
种群由一组矢量w = {w2,w2,w3,w 4}控制,并且它从Xold→的位置扩展到X*→,如下图所示。这种搜索空间的有限性导致了局部最优问题,在求解多个局部最优问题时将面临很大的挑战。为了克服这一局限性,提出了一种新的技术来扩大搜索空间的基础上的方向运动的变化:
其中ω1、ω2、ω3、ω4是矢量或标量,用于控制可扩展搜索空间。这些参数将被灵活地选择,以实现新的搜索空间扩展和收敛速度。假设ω1、ω3、ω4的值记录维度2并且其值是分布在范围[0,1]中的随机向量,而ω2的值是其值在范围[-1,1]中的随机向量,下图中以不同的迭代展示。
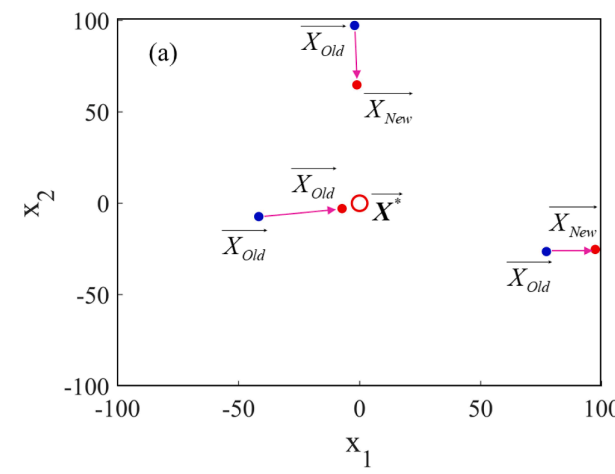
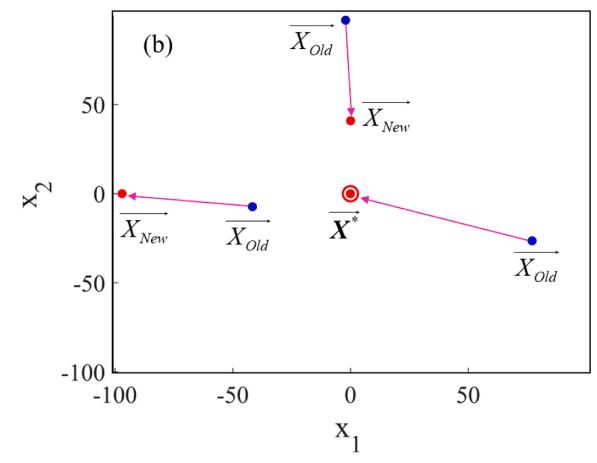
(4)模型中白蚁工蚁的运动策略
假定白蚁工蚁的数量约占殖民地总个体数的70%。设定蚁群的初始种群大小为N;因此, 表示白蚁工蚁的位置。白蚁工作者的主要职责是探索食物来源和建造庇护所管道。基于这一任务,它们的运动策略必须从它们当前的位置开始。而工蚁阶级的定向运动必须保证扩大搜索空间的能力。
通过在等式中转换 为 ,其被定义为第k次迭代时的最佳解
为了增加从 到 的运动速度,ω1,ω3和ω4的值选择为等于1:
扩展搜索空间的能力由参数ω2决定。
TLCO算法的完整伪代码如下图所示。

2.结果展示
老规矩,采用作者独创的智能优化算法APP轻松对比一下本期算法。
在23个经典函数上与其他麻雀算法、灰狼算法、鲸鱼算法、白鲸算法对比一下试试:
F1:
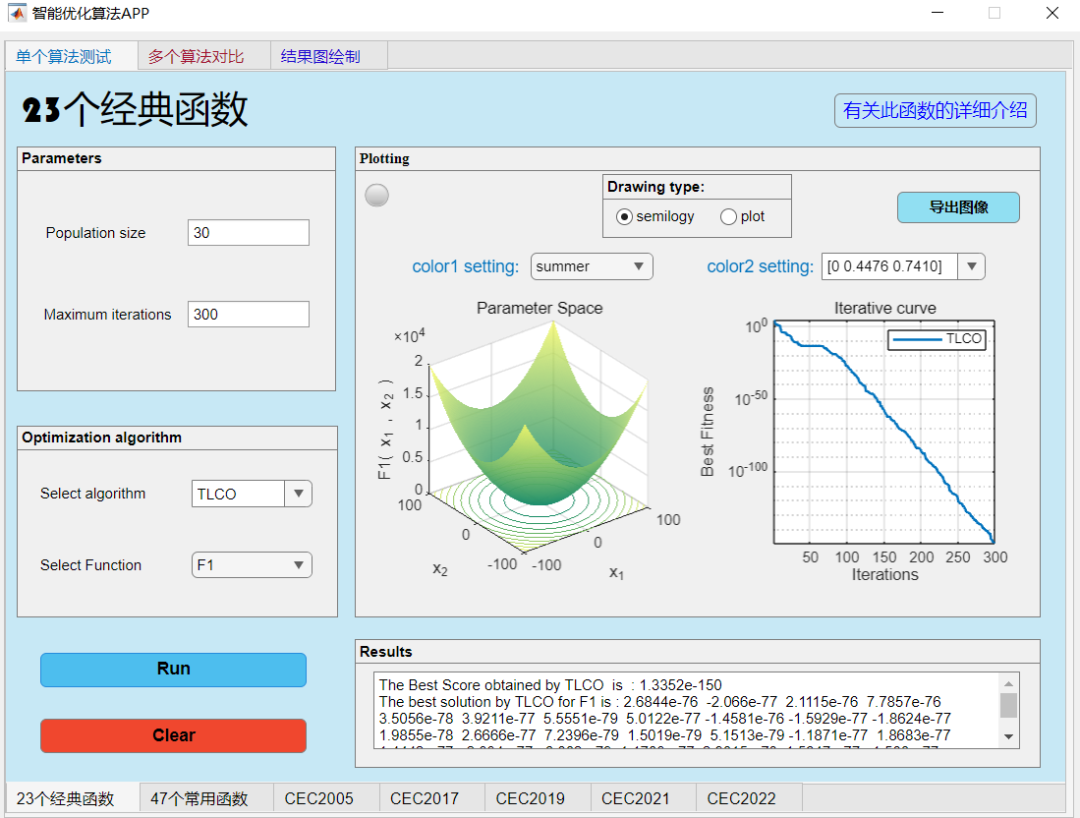
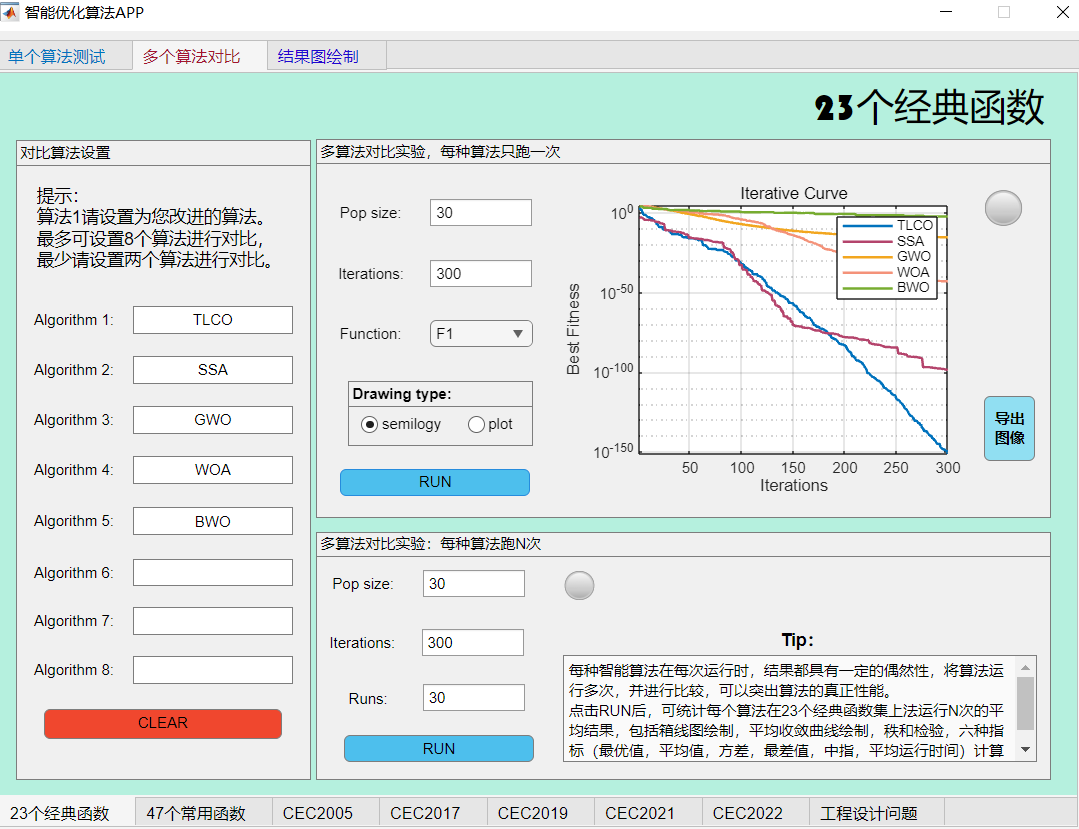
F7:
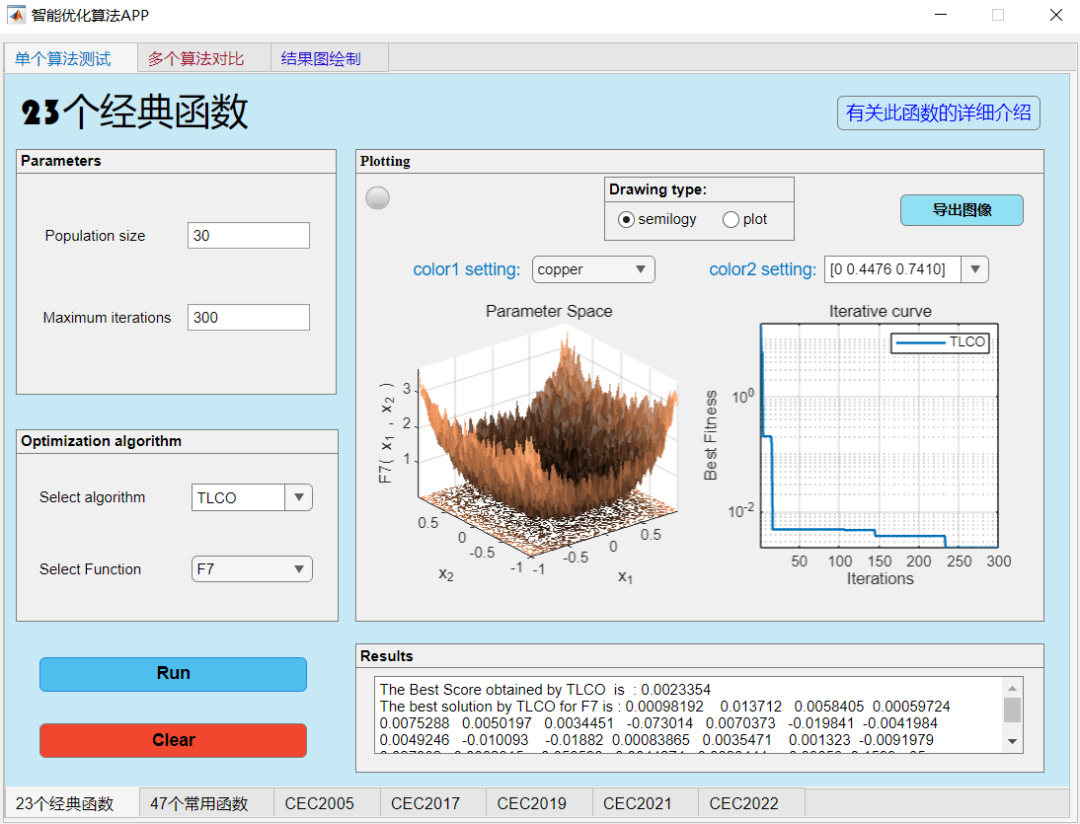
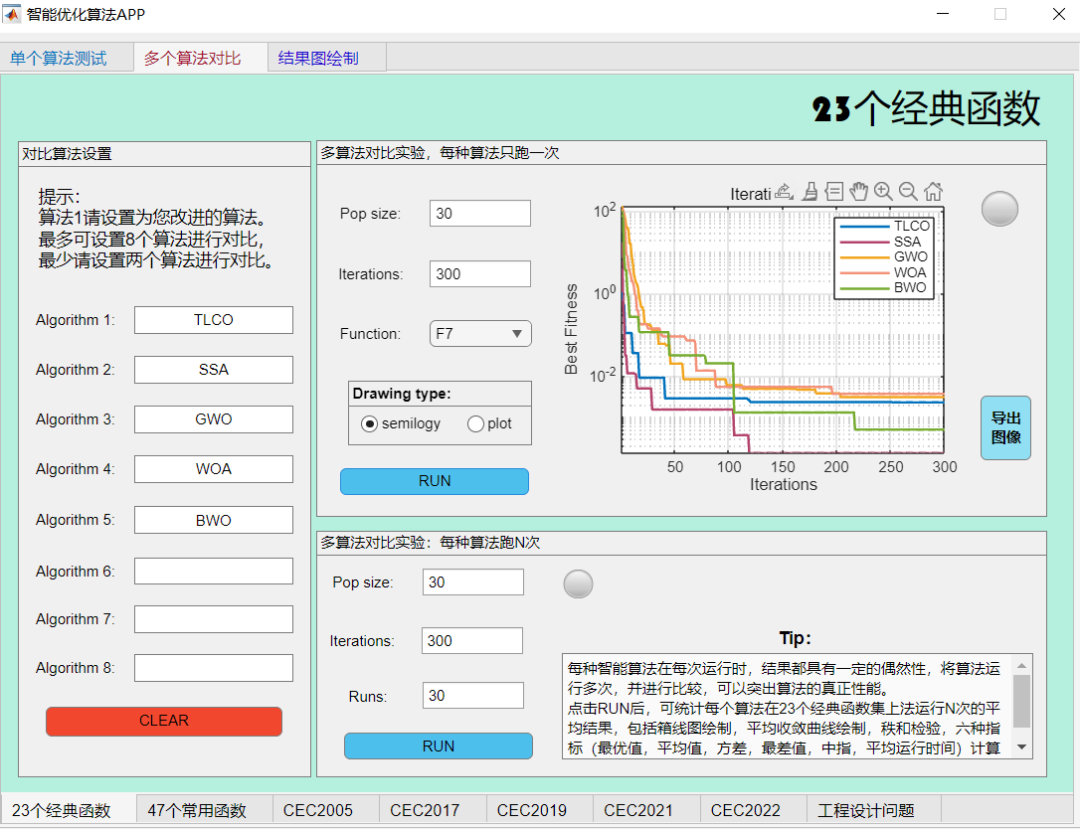
F9:
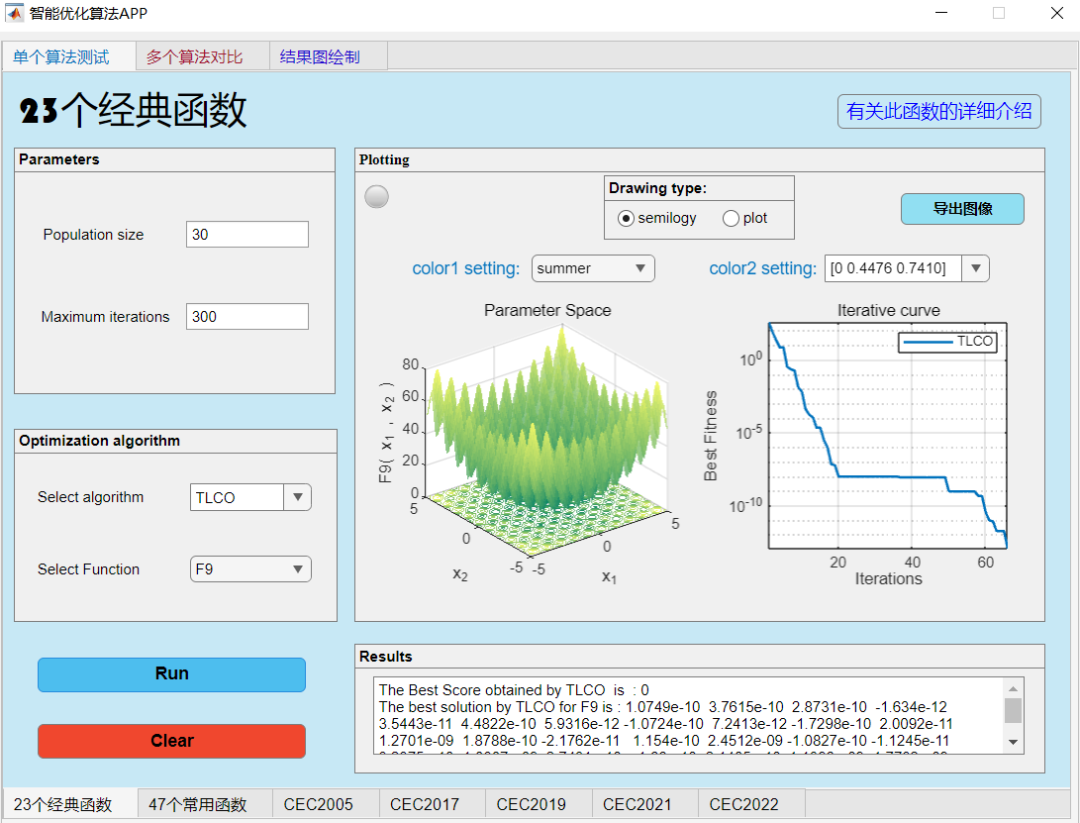
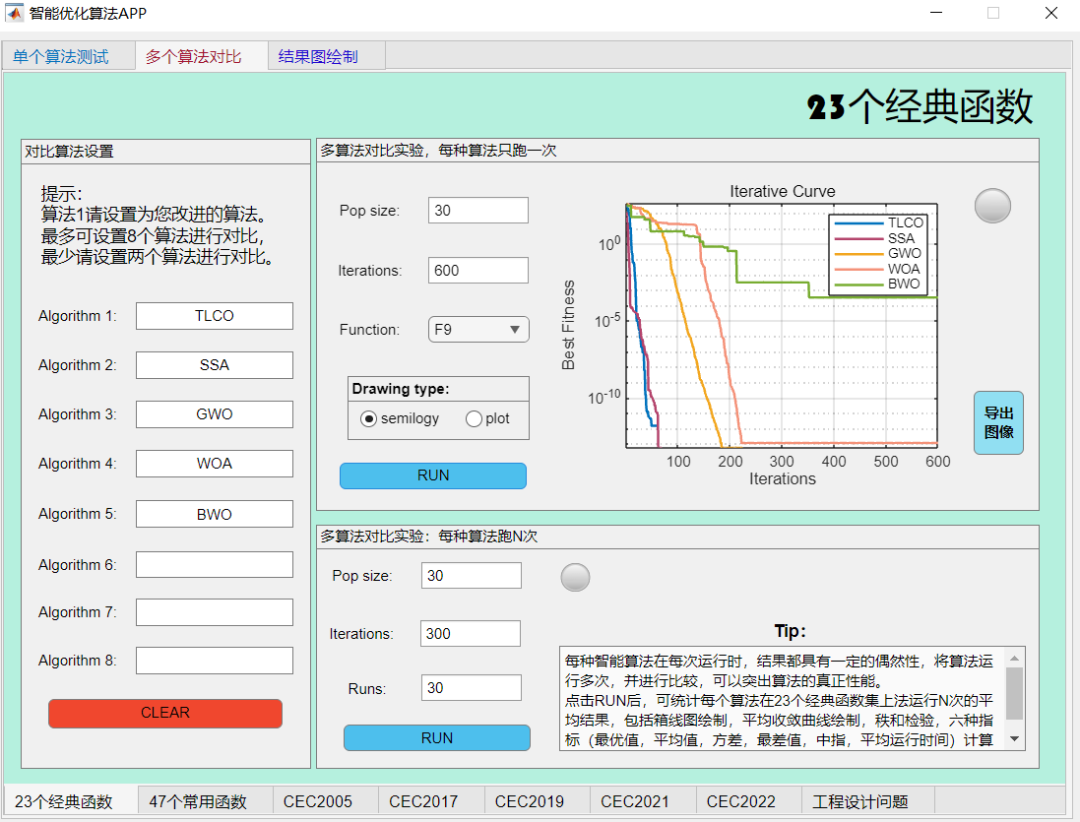
F12:
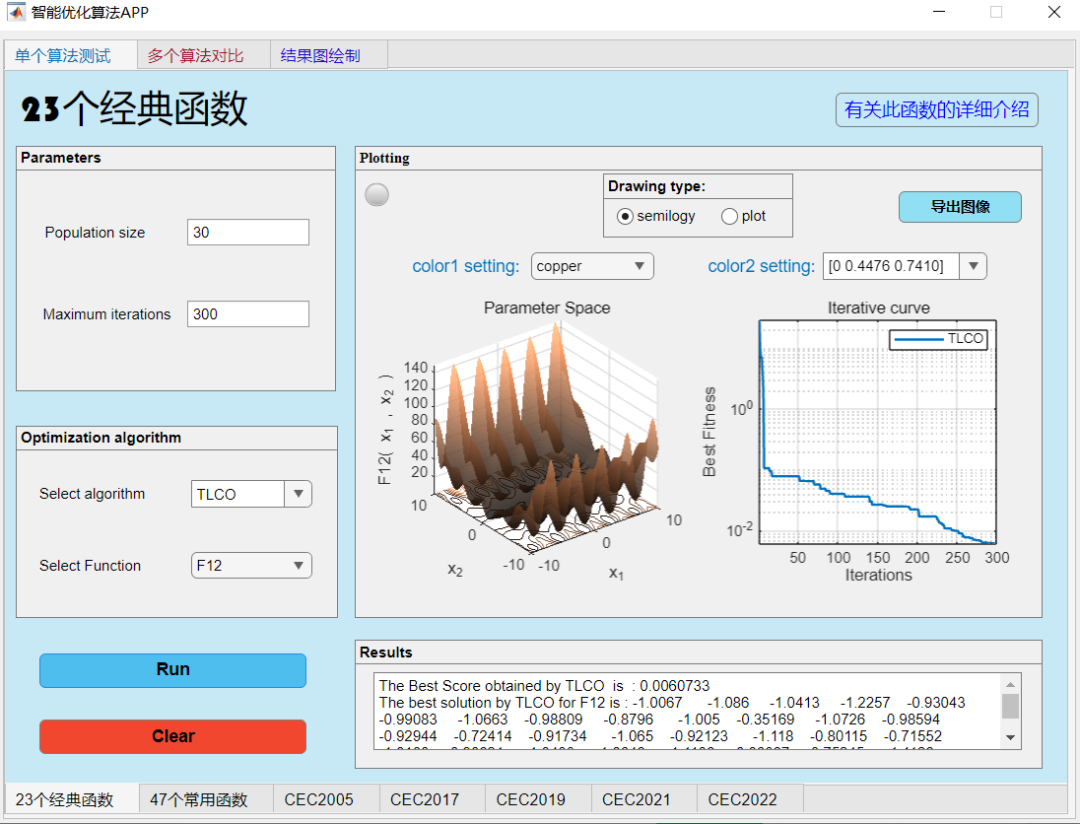
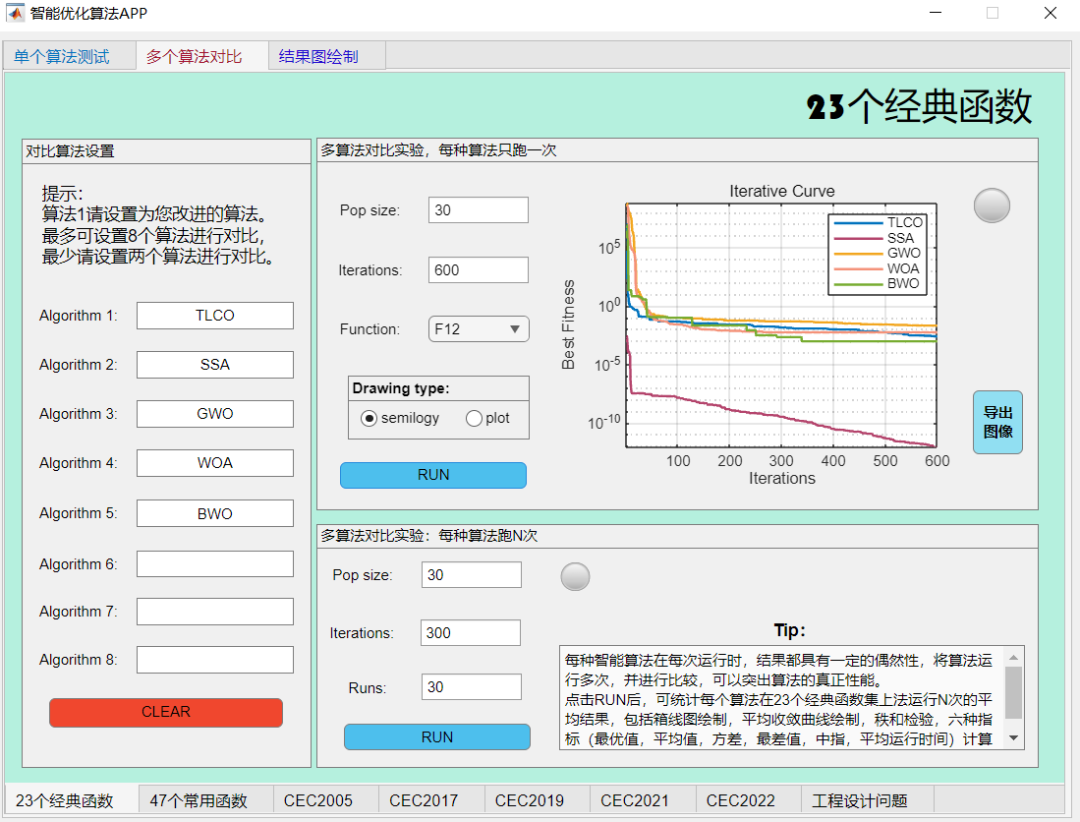
评价:算法性能处于中等。肯定比不上麻雀,但是也不算很弱,其算法公式值得借鉴!
3.MATLAB核心代码
%微信公众号搜索:淘个代码,获取更多免费代码
%禁止倒卖转售,违者必究!!!!!
%唯一官方店铺:https://mbd.pub/o/author-amqYmHBs/work
%代码清单:https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu
%%
function [gBestScore,bestPos,best_TLCO]=TLCO(NP,cycle,lb,ub,dim,fobj)
%% INITIAL DEFINATION
nvar = dim; % Dimension
Lower_B = lb; % Lower boundary
Uper_B= ub; % Uper boundary
lb = Lower_B.*ones(1,nvar); % Lower boundary (vector)
ub = Uper_B.*ones(1,nvar); % Uper boundary (vector)
trial_worker = zeros(NP,1); % Define according to Algorithm 2
trial_soldier = zeros(NP,1); % Define according to Algorithm 2
%% TERMITE LIFE CYCLE OPTIMIZER ------------------------------------------
empt.pos =[];
empt.cost = [];
particle_termine = repmat(empt,NP,1); % Define termite swarms Swarm-Opti
Int_Population = repmat(empt,NP,1); % Define initial population
%% Creare initial poppulation
for i = 1:NP
Int_Population(i).pos = lb + rand(1,nvar).*(ub-lb);
Int_Population(i).cost = fobj(Int_Population(i).pos);
end
% Assign the termite caste
particle_soldier = Int_Population;
particle_worker = Int_Population;
particle_reproductive = Int_Population;
% Find the best solution
[value, index] = min([Int_Population.cost]);
Gbest = Int_Population(index);
%% Main iterations
best_TLCO = zeros(cycle,1);
for k = 1:cycle
% Calculate the proposed beta parameter for modification step length S
beta = (0.5/cycle)*k +1.5; % Equation 6
% Calculate the timing of reproductive termites’ emergence
sigma = 1/(0.1*cycle); % Equation 17
lamda_soldier = 1/(1+exp(-sigma*(k-0.5*cycle))); % Equation 16
lamda_worker = 1- 1/(1+exp(-sigma*(k-0.5*cycle))); % Equation 15
for i = 1:round(NP)
%% The phase of Worker termite Swarm-Opti
if i <= round(0.7*NP)
% Update the new position using Eq.12
particle_worker(i).pos = particle_worker(i).pos + ...
(-1+2*rand(1)).*(rand(1,nvar) + levy_fun_TLCO(1,nvar,beta)).*abs(Gbest.pos - particle_worker(i).pos);
particle_worker(i).pos = boundary_condition(particle_worker(i).pos,lb,ub,dim);
particle_worker(i).cost = fobj( particle_worker(i).pos);
% The process of self-improvement using Algorithm 1
if particle_worker(i).cost < Int_Population(i).cost;
Int_Population(i) = particle_worker(i);
% End of Algorithm 1
if Int_Population(i).cost < Gbest.cost
Gbest = Int_Population(i); % record the best solution
end
else % Recording the wasteful movement using Algorithm 2
trial_worker(i) = trial_worker(i)+1;
end
% The phase of reproductive termites using algorithm 3
if (trial_worker(i))/cycle > lamda_worker
trial_worker(i) = 0;
A=randperm(NP);
A = [1:i-1, i+1:NP];
r1 = randi(numel(A));
A(r1)=[];
r2 = randi(numel(A));
% Update the new position using Eq.20
if Int_Population(r2).cost<Int_Population(r1).cost
particle_reproductive(i).pos = Int_Population(r1).pos + rand(1,nvar).*(Int_Population(r2).pos - Int_Population(r1).pos);
else
particle_reproductive(i).pos =Int_Population(r1).pos - rand(1,nvar).*(Int_Population(r2).pos - Int_Population(r1).pos);
end
particle_reproductive(i).pos = boundary_condition(particle_reproductive(i).pos,lb,ub,dim);
particle_reproductive(i).cost = fobj( particle_reproductive(i).pos);
% The process of self-improvement using Algorithm 1
if particle_reproductive(i).cost < Int_Population(i).cost
Int_Population(i) = particle_reproductive(i);
% End of Algorithm 1
if Int_Population(i).cost < Gbest.cost
Gbest = Int_Population(i); % record the best solution
end
else
% Update the new position using Eq.21
particle_reproductive(i).pos = lb + rand(1,nvar).*(ub-lb);
end
particle_worker(i) = particle_reproductive (i);
% End of Algorithm 3
end
end % End of the termite worker phase
%% -------------------------------------------------------------------
if i >round(0.7*NP) && i <= round(NP)
% Update the new position using Eq.14
particle_soldier(i).pos =2*rand(1).*Gbest.pos +...
(-1+2*rand(1)).*abs( particle_soldier(i).pos - (levy_fun_TLCO(1,nvar,beta).*Gbest.pos)) ;
particle_soldier(i).pos = boundary_condition(particle_soldier(i).pos,lb,ub,dim);
particle_soldier(i).cost = fobj( particle_soldier(i).pos);
% The process of self-improvement using Algorithm 1
if particle_soldier(i).cost < Int_Population(i).cost;
Int_Population(i) = particle_soldier(i);
% End of Algorithm 1
if Int_Population(i).cost < Gbest.cost
Gbest = Int_Population(i);
end
else % Recording the wasteful movement using Algorithm 2
trial_soldier(i) = trial_soldier(i)+1 ;
end
% The phase of reproductive termites using algorithm 3
if (trial_soldier(i))/cycle> lamda_soldier
trial_soldier(i)=0;
A = randperm(NP,0.7*NP);
A = [0.7*NP:i-1, i+1:NP];
r1 = randi(numel(A)); %
A(r1)=[];
r2 = randi(numel(A));
% Update the new position using Eq.20
if Int_Population(r2).cost<Int_Population(r1).cost
particle_reproductive(i).pos = Int_Population(r1).pos + rand(1,nvar).*(Int_Population(r2).pos - Int_Population(r1).pos);
else
particle_reproductive(i).pos = Int_Population(r1).pos - rand(1,nvar).*(Int_Population(r2).pos - Int_Population(r1).pos);
end
particle_reproductive(i).pos = boundary_condition(particle_reproductive(i).pos,lb,ub,dim);
particle_reproductive(i).cost = fobj( particle_reproductive(i).pos);
% The process of self-improvement using Algorithm 1
if particle_reproductive(i).cost < Int_Population(i).pos
Int_Population(i) = particle_reproductive(i);
% End of Algorithm 1
if Int_Population(i).cost < Gbest.cost
Gbest = Int_Population(i);% record the best solution
end
else
% Update the new position using Eq.21
particle_reproductive(i).pos = lb + rand(1,nvar).*(ub-lb);
end
particle_soldier(i) = particle_reproductive(i);
end
% End of Algorithm 3
end % End of termite soldier phase
end
best_TLCO(k) = Gbest.cost;
end % end of cycle
gBestScore = Gbest.cost;
bestPos = Gbest.pos;
end
%%
function [output] = boundary_condition(X,Lb,Ub,dim)
for i = 1:dim
if X(i) > Ub(i)% lon hon can tren
X(i) = Lb(i) + rand.*(Ub(i)-Lb(i));
end
if X(i) < Lb(i)% nho hon can duoi
X(i) = Lb(i) + rand.*(Ub(i)-Lb(i));
end
end
output = X;
end
function [z] = levy_fun_TLCO(n,m,beta)
% This function implements Levy's flight.
% Input parameters
% n -> Number of steps
% m -> Number of Dimensions
% beta -> Power law index % Note: 1 < beta < 2
% Output
% z -> 'n' levy steps in 'm' dimension
% n = 10;
% m = 30;
% beta = 1.4;
num = gamma(1+beta)*sin(pi*beta/2); % used for Numerator
den = gamma((1+beta)/2)*beta*2^((beta-1)/2); % used for Denominator
sigma_u = (num/den)^(1/beta);% Standard deviation
u = random('Normal',0,sigma_u^2,n,m);
v = random('Normal',0,1,n,m);
z =( u./(abs(v).^(1/beta)));
end
4.参考文献
[1]Minh H L, Sang-To T, Theraulaz G, et al. Termite life cycle optimizer[J]. Expert Systems with Applications, 2023, 213: 119211.
完整代码获取
点击下方卡片,获取代码






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










