注:该算法已按照智能优化算法APP标准格式进行整改,可直接集成到APP中,方便大家与自己的算法进行对比。
向量加权平均(weIghted meaN of vectOrs, INFO)是一种新型的优化器,它将权均值思想应用于实体结构,通过更新规则、向量组合和局部搜索三个核心步骤更新向量的位置。更新规则阶段是基于均值定律和收敛加速来生成新向量。向量组合阶段将得到的向量与更新规则进行组合,以获得有希望的解。改进了算法中的更新规则和矢量组合步骤,提高了勘探开发能力。此外,局部搜索阶段有助于该算法避免低精度解,提高挖掘和收敛性。
该成果于2023年发表在计算机领域2区SCI期刊“Engineering Applications Of Artificial Intelligence”上,目前被引20次。

1.算法原理
(1)加权平均数的数学定义
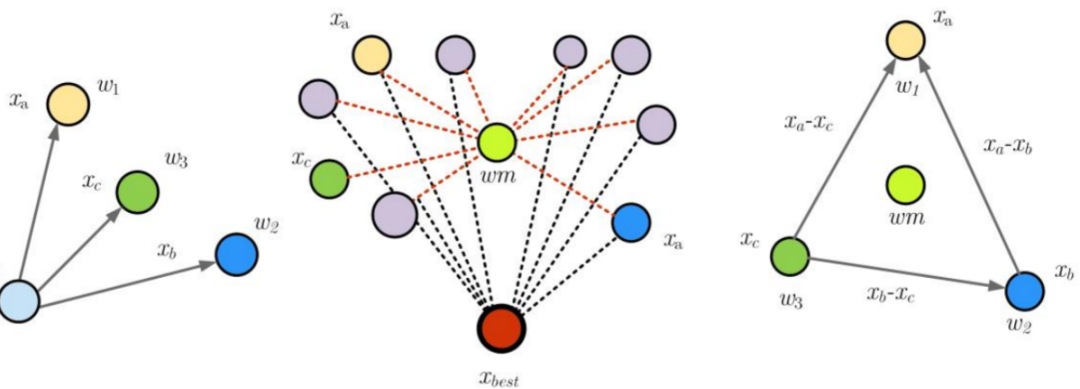
一组向量的平均值被描述为它们的位置(Xi)的平均值,由向量的适应度(wi)加权。事实上,使用这个概念是因为它的简单性和易于实现。下图描述了一组解(向量)的加权平均值,其中具有较大权重的解在计算解的加权平均值时更有效。
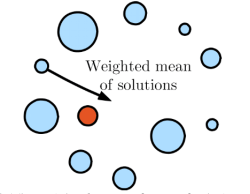
加权平均值(WM)的公式由等式定义:
其中N是向量的数目。
为了提供更好的解释,WM可以被认为是两个矢量,如等式所示:
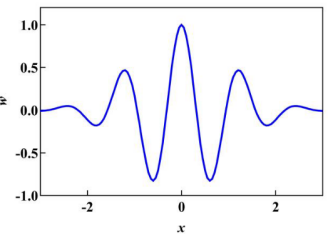
在这项研究中,每个向量的权重是基于小波函数(WF)计算的。通常,小波是用于通过复合振荡函数的平移和膨胀(即母小波)具有有限周期。该函数用于在优化过程中创建有效的波动。下图显示了本研究中使用的母小波,其定义为:
其中,w是一个常数,称为膨胀参数。
下图显示了三个矢量,它们之间的差异如图所示。
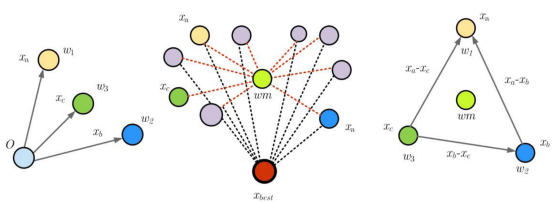
向量的加权平均值由公式计算:
其中, , , ,
其中f(x)表示向量x的适应度函数。
式中rand(0,1)为[0,1]范围内的随机数,Xi0为表示在初始阶段中的第i位置。
(2)向量加权均值(INFO)算法
向量加权平均值算法(INFO)是一种基于种群的优化算法,它计算搜索空间中一组向量的加权平均值。在所提出的算法中,人口是由一组向量,证明可能的解决方案。INFO算法在几个连续的代中找到最优解。
三个运算符在每一代中更新向量的位置:阶段1:更新规则;阶段2:向量组合;阶段3:局部搜索
这里,最小化目标函数的问题被认为是一个例子。
(3)初始化阶段
INFO算法由D维搜索域中的Np个向量的群体 。在这一步中,为INFO算法引入和定义一些控制参数。有两个主要参数:加权平均因子和比例因子。
一般来说,缩放率用于通过更新规则算子放大所获得的向量,这取决于搜索域的大小。该因子用于缩放向量的加权平均值。它的值是基于问题的可行搜索空间指定的,并根据指数公式减少。这两个参数不需要由用户调整并且基于生成而动态地改变。INFO算法使用一种称为随机生成的简单方法来生成初始向量。
(4)更新规则阶段
在INFO算法中,规则更新算子在搜索过程中增加了种群的多样性。该运算符使用向量的加权平均值来创建新的向量。实际上,该运算符将INFO算法与其他算法区分开来,并且由两个主要部分组成。在第一部分中,基于均值的规则是从一组随机向量的加权均值中提取的。基于均值的方法从随机初始解开始,并使用一组随机选择的向量的加权均值信息移动到下一个解。第二部分是收敛加速,提高了算法的收敛速度,使算法的性能更接近最优解。
一般来说,INFO首先使用一组随机选择的差分向量来获得向量的加权平均值,而不是将当前向量移向更好的解决方案。在这项工作中,增加人口的多样性被认为是基于最好,更好和最坏的解决方案的平均规则。应该注意的是,更好的解决方案是从前5个解决方案中随机确定的(关于目标函数值)。因此,基于平均值的规则被引导到MeanRule,如下式定义:
其中,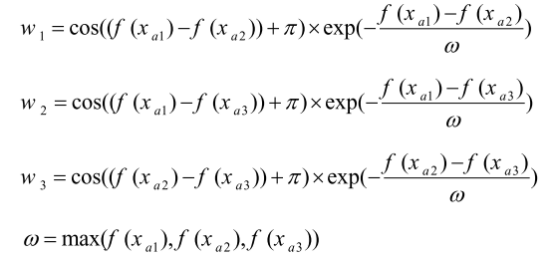
其中,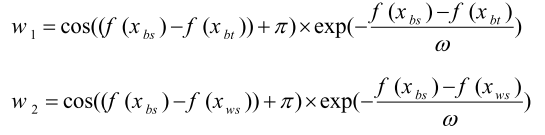
其中f(x)是目标函数的值; 是从范围[1,NP]中随机选择的不同整数; 是一个常数,具有很小的值; randn是正态分布的随机值; xbs,xbt和xws分别是第g代种群中所有向量的最佳、较好和最差解。实际上,这些解是在每次迭代时对解进行排序后确定的。r是范围[0,0.5]内的随机数; w1、w2和w3是用于计算向量的加权平均值的三个WF,这有助于所提出的INFO算法在解空间中全局搜索。
其中,Maxg是最大生成次数。
在规则更新算子中加入收敛加速部分,利用最优向量在搜索空间中移动当前向量,提高全局搜索能力。在INFO算法中,假定最优解是最接近全局最优解的解。事实上,CA帮助向量向更好的方向移动。将下式乘以范围rand[0,1]内的随机数,以确保每个向量在INFO中的每一代中具有不同的步长:
其中randn是具有正态分布的随机数。
最后,使用下式计算新向量:
优化算法通常应该全局搜索以发现搜索域的有希望的空间(探索阶段)。因此,使用以下方案来定义基于xbs,xbt,xgl和xgal的所提出的更新规则:
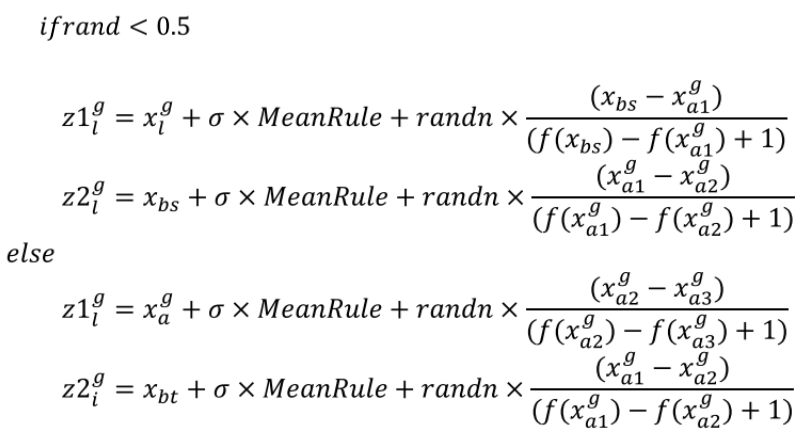
其中,z1gl和z2gl是第g代中的新矢量;并且, 是矢量的缩放率,如下式所定义的:
其中c和d是分别等于2和4的常数。值得注意的是,对于参数k的大值,当前位置倾向于偏离向量的加权平均值(探索搜索),而该参数的小值迫使当前位置向向量的加权平均值移动(利用搜索)。
(5)矢量合并级
在这项研究中,为了增强INFO中的种群多样性,将前一节中计算的两个矢量(z1gl和z2gl)与矢量xgl结合,根据下式,关于条件xgl <0.5,以生成新的矢量ugl:
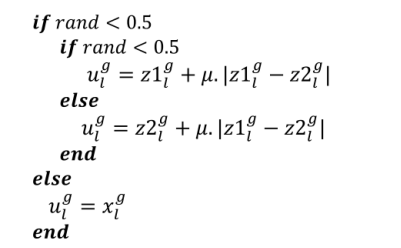
其中,ugi是使用第g代中的向量组合获得的向量;并且u等于0.05×randn。
所提出的INFO算法伪代码如图所示:

INFO的流程图如下所示:
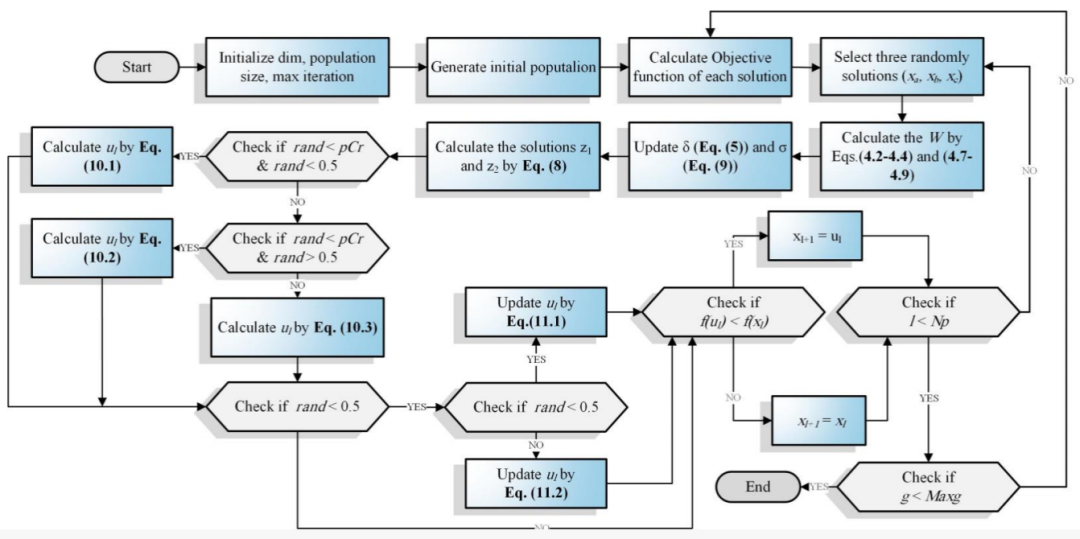
2.结果展示
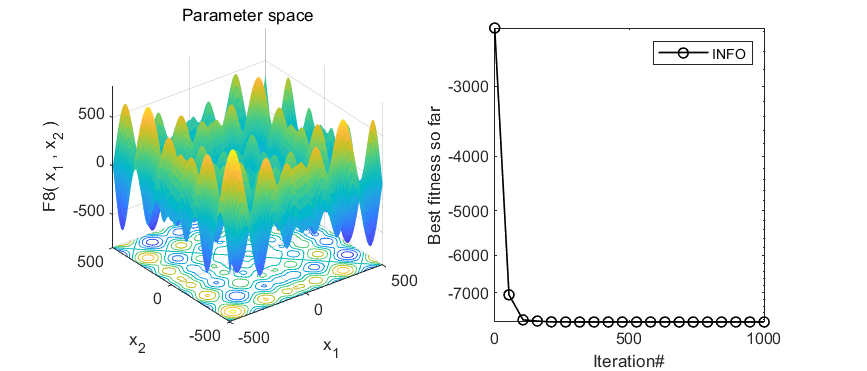
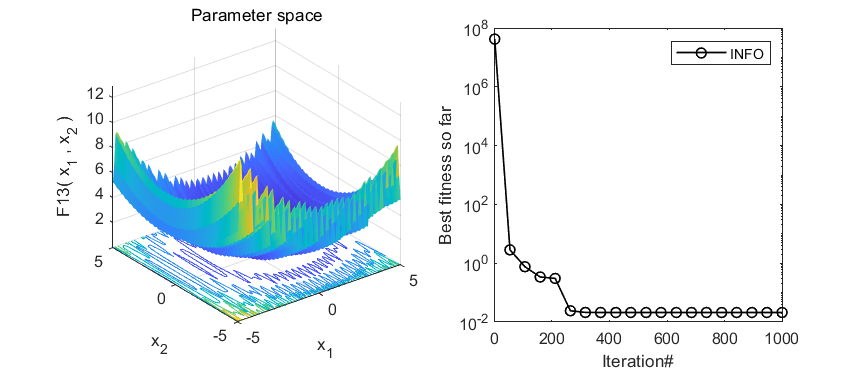
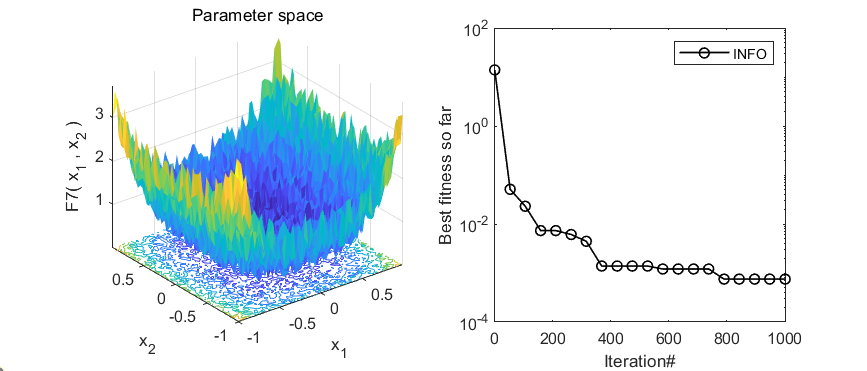
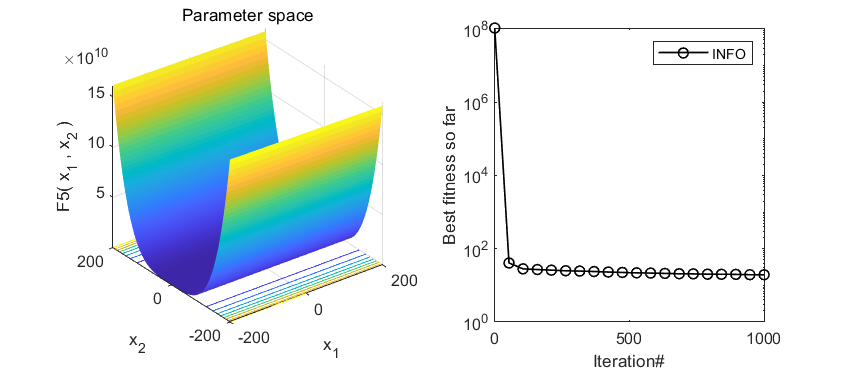
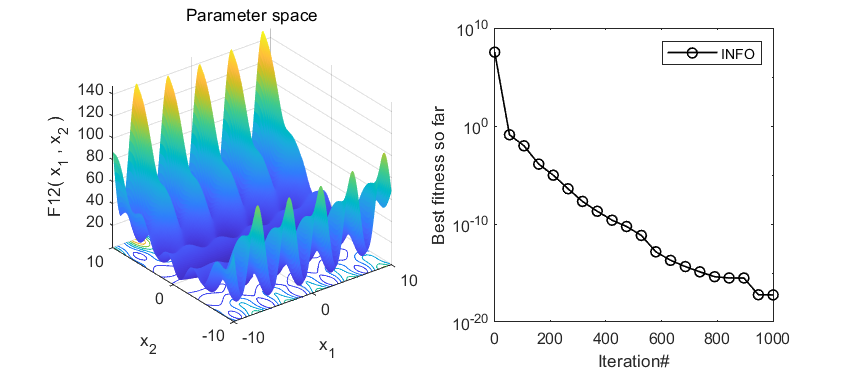
3.MATLAB核心代码
function [Best_Cost,Best_X,Convergence_curve]=INFO(nP,MaxIt,lb,ub,dim,fobj)
%% Initialization
Cost=zeros(nP,1);
M=zeros(nP,1);
X=initialization(nP,dim,ub,lb);
for i=1:nP
Cost(i) = fobj(X(i,:));
M(i)=Cost(i);
end
[~, ind]=sort(Cost);
Best_X = X(ind(1),:);
Best_Cost = Cost(ind(1));
Worst_Cost = Cost(ind(end));
Worst_X = X(ind(end),:);
I=randi([2 5]);
Better_X=X(ind(I),:);
Better_Cost=Cost(ind(I));
%% Main Loop of INFO
for it=1:MaxIt
alpha=2*exp(-4*(it/MaxIt)); % Eqs. (5.1) & % Eq. (9.1)
M_Best=Best_Cost;
M_Better=Better_Cost;
M_Worst=Worst_Cost;
for i=1:nP
% Updating rule stage
del=2*rand*alpha-alpha; % Eq. (5)
sigm=2*rand*alpha-alpha; % Eq. (9)
% Select three random solution
A1=randperm(nP);
A1(A1==i)=[];
a=A1(1);b=A1(2);c=A1(3);
e=1e-25;
epsi=e*rand;
omg = max([M(a) M(b) M(c)]);
MM = [(M(a)-M(b)) (M(a)-M(c)) (M(b)-M(c))];
W(1) = cos(MM(1)+pi)*exp(-(MM(1))/omg); % Eq. (4.2)
W(2) = cos(MM(2)+pi)*exp(-(MM(2))/omg); % Eq. (4.3)
W(3)= cos(MM(3)+pi)*exp(-(MM(3))/omg); % Eq. (4.4)
Wt = sum(W);
WM1 = del.*(W(1).*(X(a,:)-X(b,:))+W(2).*(X(a,:)-X(c,:))+ ... % Eq. (4.1)
W(3).*(X(b,:)-X(c,:)))/(Wt+1)+epsi;
omg = max([M_Best M_Better M_Worst]);
MM = [(M_Best-M_Better) (M_Best-M_Better) (M_Better-M_Worst)];
W(1) = cos(MM(1)+pi)*exp(-MM(1)/omg); % Eq. (4.7)
W(2) = cos(MM(2)+pi)*exp(-MM(2)/omg); % Eq. (4.8)
W(3) = cos(MM(3)+pi)*exp(-MM(3)/omg); % Eq. (4.9)
Wt = sum(W);
WM2 = del.*(W(1).*(Best_X-Better_X)+W(2).*(Best_X-Worst_X)+ ... % Eq. (4.6)
W(3).*(Better_X-Worst_X))/(Wt+1)+epsi;
% Determine MeanRule
r = unifrnd(0.1,0.5);
MeanRule = r.*WM1+(1-r).*WM2; % Eq. (4)
if rand<0.5
z1 = X(i,:)+sigm.*(rand.*MeanRule)+randn.*(Best_X-X(a,:))/(M_Best-M(a)+1);
z2 = Best_X+sigm.*(rand.*MeanRule)+randn.*(X(a,:)-X(b,:))/(M(a)-M(b)+1);
else % Eq. (8)
z1 = X(a,:)+sigm.*(rand.*MeanRule)+randn.*(X(b,:)-X(c,:))/(M(b)-M(c)+1);
z2 = Better_X+sigm.*(rand.*MeanRule)+randn.*(X(a,:)-X(b,:))/(M(a)-M(b)+1);
end
% Vector combining stage
u=zeros(1,dim);
for j=1:dim
mu = 0.05*randn;
if rand <0.5
if rand<0.5
u(j) = z1(j) + mu*abs(z1(j)-z2(j)); % Eq. (10.1)
else
u(j) = z2(j) + mu*abs(z1(j)-z2(j)); % Eq. (10.2)
end
else
u(j) = X(i,j); % Eq. (10.3)
end
end
% Local search stage
if rand<0.5
L=rand<0.5;v1=(1-L)*2*(rand)+L;v2=rand.*L+(1-L); % Eqs. (11.5) & % Eq. (11.6)
Xavg=(X(a,:)+X(b,:)+X(c,:))/3; % Eq. (11.4)
phi=rand;
Xrnd = phi.*(Xavg)+(1-phi)*(phi.*Better_X+(1-phi).*Best_X); % Eq. (11.3)
Randn = L.*randn(1,dim)+(1-L).*randn;
if rand<0.5
u = Best_X + Randn.*(MeanRule+randn.*(Best_X-X(a,:))); % Eq. (11.1)
else
u = Xrnd + Randn.*(MeanRule+randn.*(v1*Best_X-v2*Xrnd)); % Eq. (11.2)
end
end
% Check if new solution go outside the search space and bring them back
New_X= BC(u,lb,ub);
New_Cost = fobj(New_X);
if New_Cost<Cost(i)
X(i,:)=New_X;
Cost(i)=New_Cost;
M(i)=Cost(i);
if Cost(i)<Best_Cost
Best_X=X(i,:);
Best_Cost = Cost(i);
end
end
end
% Determine the worst solution
[~, ind]=sort(Cost);
Worst_X=X(ind(end),:);
Worst_Cost=Cost(ind(end));
% Determine the better solution
I=randi([2 5]);
Better_X=X(ind(I),:);
Better_Cost=Cost(ind(I));
% Update Convergence_curve
Convergence_curve(it)=Best_Cost;
% Show Iteration Information
disp(['Iteration ' num2str(it) ',: Best Cost = ' num2str(Best_Cost)]);
end
end
function X = BC(X,lb,ub)
Flag4ub=X>ub;
Flag4lb=X<lb;
X=(X.*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
end
4.参考文献
[1]Wan T H, Tsang C W, Hui K, et al. Anomaly detection of train wheels utilizing short-time Fourier transform and unsupervised learning algorithms[J]. Engineering Applications of Artificial Intelligence, 2023, 122: 106037.
完整代码获取
点击下方卡片,获取代码后台回复关键词:
TGDM819





















 705
705

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










