【数字信号处理】基于DFT的滤波系列4之加窗(含MATLAB代码)

四、基于DFT的(理想)滤波

加窗以减少频谱泄漏

在上面的例子中，整数次谐波被用来产生理想中的示例。这意味着一个完整的整数周期适合正在使用的样本数。一个明显的问题是，如果使用非整数周期数（以及谐波）会怎样？答案是远没有那么有效。

在现实世界中，从这个意义上说，数据通常并不理想，这就是可以使用时域数据的窗口化来帮助改进频谱的地方，如下例所示。

此示例使用Blackman窗，在 Matlab 中可使用blackman()函数——其他窗函数有Hamming和Hann窗。

下图显示了由3.3次谐波的信号和11.6次谐波的噪声组成的合成数据。

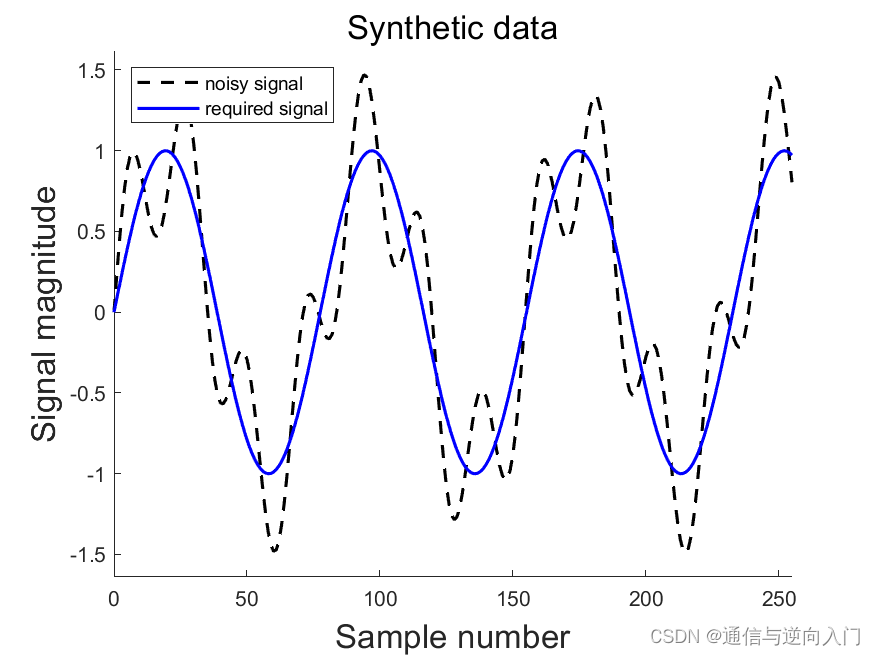
• 图1

应该对 DFT 的操作有足够的了解，这意味着当将信号与不同频率的 DFT 基函数进行比较时，许多频率的DFT基函数将返回非零值。这与信号处于整数谐波时发生的情况形成对比，也就是只有一个基函数将返回非零值——因为所有其他模板都将与信号正交。

该信号的频率分析结果如下图所示。不再显示数据谐波处的单个值，因为它不是整数。所发生的情况是，信号中的能量在以信号频率为中心的同时被“涂抹”在众多谐波上。这种现象被称为频谱泄