利用SVD简化数据——奇异值分解

基础知识

奇异值分解 
优点：简化数据，去除噪声，提高算法的结果。
缺点：数据的转换可能难以理解。
适用数据类型：数值型数据。

作用：数据降维，压缩存储。通过抽取特征数据，
从而去除噪声和冗余数据，达到压缩数据的目的。

应用的主要方面有：隐形语义的索引，推荐引擎，
数据压缩。

下面我们就来具体看看SVD的应用有哪些：

●最早的SVD应用之-就是信息检索,我们称利用SVD的方法为隐性语义索引(LSI) 或隐性语义分析(LSA) 。
●隐性语义索引(Latent Semantic Indexing, LSI) :矩阵=文档+词语
●矩阵存储文档中的词语，通过应用SVD构建奇异值,这些奇异值代表了文档中的概念或主题，从而方便文档搜索。

SVD的另一个应用就是推荐系统。简单版本的推荐系统能够计算项或者人之间的相似度。更
先进的方法则先利用SVD从数据中构建一个主题空间，然后再在该空间下计算其相似度。考虑图
14-1中给出的矩阵，它是由餐馆的菜和品菜师对这些菜的意见构成的。品菜师可以采用1到5之间
的任意一个整数来对菜评级。如果品菜师没有尝过某道菜，则评级为0。


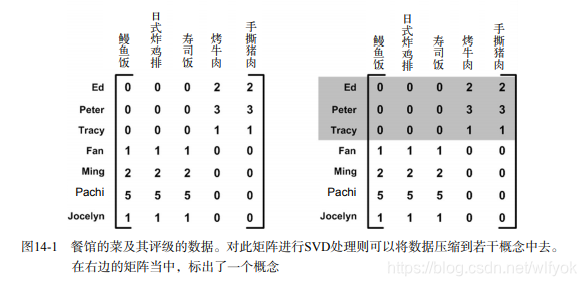
在介绍完基础知识和应用背景之后，我们引入奇异值分解的原理，在数学上保证其成立。

奇异值分解的原理

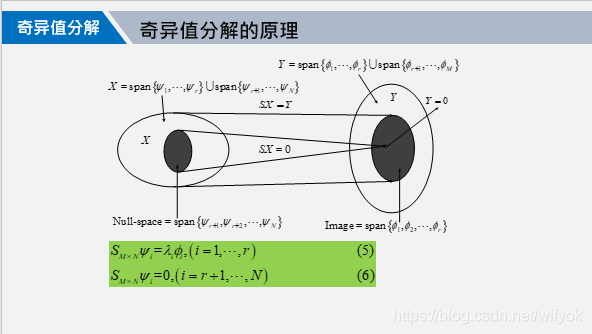
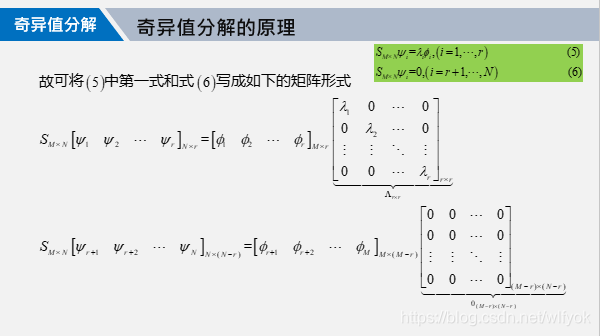
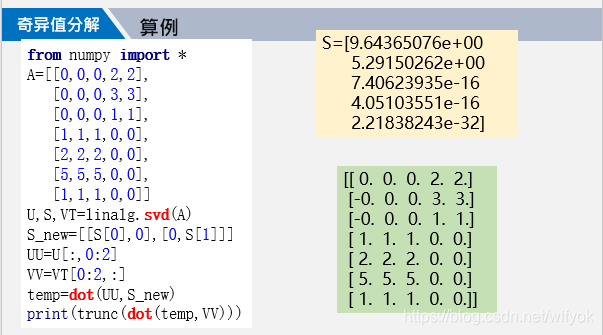
python函式库中自带有svd分解的函数，读者只需要按照使用方法调用即可。
从上面的这个算例中看出，我们对给定的矩阵A进行分解之后，可以A压缩为三个所需存储空间更小的矩阵，且才还原之后数据的几乎可以做到没有损失程度，这是我们所希望看到的结果！


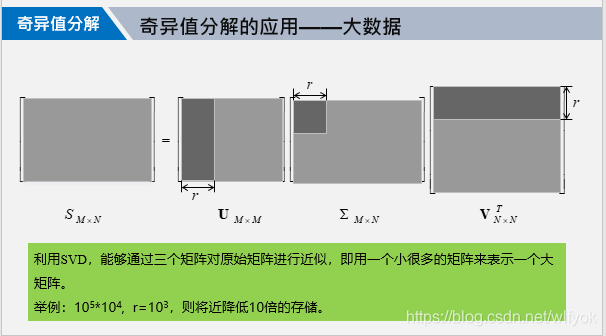
关于特征矩阵的，就是中间的那个对角矩阵的维度的取值，我们一般是将λ进行归一化，然后去其中累计已经超过0.9的哪些特征值作为A=svd中v的维度。当然如果你希望数据还原更精确，你可以再取大一些，只不过这会增大存储的空间。具体的来说，如果A的维度是mn的，那么s，v，d三个矩阵的维度通过奇异值分解就可以变为mr，rr，rn。

对于基于奇异值分解对数据进行压缩存储基本上理解到这里就可以了，代码也就是和之前讲解的图上的差不多，为了读者能更深入理解，我们再介绍一个推荐度的算法。

基于协同过滤的搜索引擎

协同过滤：通过用户和其他用户的数据对比来实现推荐。
例如：我们对某个用户喜欢的电影进行预测，从而判断一部新的影片是否会喜欢。(这里就涉及到了相似度的计算)。
相似度：物品相似度和用户相似的。