题目描述
小轩很喜欢稀奇古怪的事情,所以经常做一些奇怪的梦,有一天晚上,小轩突然梦见自己是学生会会长,要布置一个会场,假设会场是一个n × n的矩阵,为了灯光效果,同一行和同一列只能装一个彩灯,为了节约成本,小轩只购买了5个相同的彩灯。现在小轩问你,摆放这5个彩灯有多少种合理的方案。
如下是一个5 × 5的矩阵。
输入
输入一个n,1 <= n <= 100.
输出
输出合理方案数,如果不存在合理的方案数,则输出0.
样例输入 Copy
5
样例输出 Copy
120
来源/分类
概念:
排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
公式:
对于本题:
"假设会场是一个n × n的矩阵,小轩只购买了5个相同的彩灯,摆放这5个彩灯有多少种合理的方案。"思路就是
先从n行里面选出5行来放彩灯(不考虑排序)。对于选出来的5行:每行n个里面选5个的排列(考虑排序)
注意long long
且输出的时候sum/120*sum,这样先除后乘
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ll n;
cin>>n;
ll sum=1;
for(int i=0;i<5;i++)
{
sum*=(n-i);
}
if(n<5)cout<<"0"<<endl;
else cout<<sum/120*sum<<endl;
return 0;
}




 该博客讨论了一个编程挑战,涉及在n×n矩阵中放置5个彩灯,每行和每列只能有一个。通过计算排列组合,得出放置方案数。题目给出了5×5矩阵的示例,并提供了C++代码实现。解决方案的关键在于理解排列和组合的概念,以及如何计算特定数量的选择和排列。
该博客讨论了一个编程挑战,涉及在n×n矩阵中放置5个彩灯,每行和每列只能有一个。通过计算排列组合,得出放置方案数。题目给出了5×5矩阵的示例,并提供了C++代码实现。解决方案的关键在于理解排列和组合的概念,以及如何计算特定数量的选择和排列。
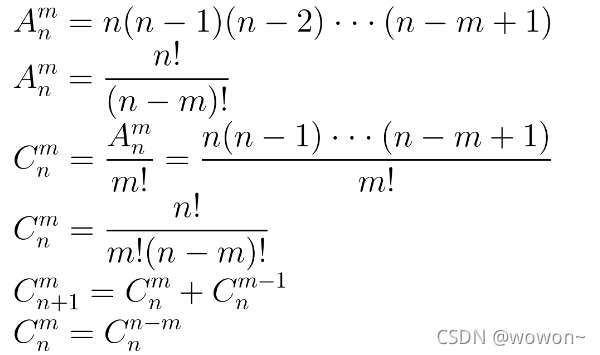
















 830
830

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








