矩阵的秩
对于一个
M
×
N
M \times N
M×N的矩阵A,其秩R(A)为线性无关的行向量(列向量)的数量。在空间中,秩表示矩阵的行向量或列向量所张成的空间的维度。
比如有矩阵并化为行最简矩阵:
[
1
2
1
−
2
2
3
0
−
1
1
−
1
−
5
7
]
∼
[
1
0
−
3
4
0
1
2
−
3
0
0
0
0
]
\begin{bmatrix} 1 &2 &1 & -2\\ 2& 3& 0& -1\\ 1& -1& -5&7 \end{bmatrix} \sim \begin{bmatrix} 1 &0 &-3 & 4\\ 0& 1& 2& -3\\ 0& 0& 0&0 \end{bmatrix}
⎣⎡12123−110−5−2−17⎦⎤∼⎣⎡100010−3204−30⎦⎤
所以上述的矩阵秩为2,表示矩阵中的所有向量都可以由
[
1
0
0
]
\begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}
⎣⎡100⎦⎤和
[
0
1
0
]
\begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}
⎣⎡010⎦⎤线性表示,相当于矩阵张成了二维的空间。
对于
[
1
1
0
2
−
1
−
1
0
−
2
]
\begin{bmatrix} 1 &1 &0 & 2\\ -1& -1& 0& -2\\ \end{bmatrix}
[1−11−1002−2],按行看,行向量在4维空间中关于原点对称;从列来看,列向量在2维空间中4个点位于同一条直线。所以该矩阵只张成了一个1维的空间,所以秩为1,列向量都可以由
[
1
−
1
]
\begin{bmatrix} 1 \\ -1\\ \end{bmatrix}
[1−1]线性表示。
(1)行秩等于列秩,所以矩阵的秩不会超过行向量或列向量的行数和列数,所以有关系:
R
(
A
)
≤
min
(
M
,
N
)
R(A)\leq \min(M,N)
R(A)≤min(M,N)
(2)
R
(
A
B
)
≤
min
(
R
(
A
)
,
R
(
B
)
)
R(AB)\leq \min(R(A),R(B))
R(AB)≤min(R(A),R(B))
两个不同秩的矩阵相乘,得到的矩阵的秩不会超过两者秩的最小值。
比如:
[
1
0
0
0
]
[
1
0
0
0
1
0
]
=
[
1
0
0
0
0
0
]
\begin{bmatrix} 1 &0 \\ 0& 0\\ \end{bmatrix}\begin{bmatrix} 1 &0&0\\ 0& 1&0\\ \end{bmatrix}=\begin{bmatrix} 1 &0 &0 \\ 0& 0& 0\\ \end{bmatrix}
[1000][100100]=[100000]
因为多余的维度会被乘0而消失,当然秩也不一定会等于
min
(
R
(
A
)
,
R
(
B
)
)
\min(R(A),R(B))
min(R(A),R(B)),因为可能相乘的时候有数的位置不一定对应有数的位置,导致都变为0,使得秩下降。
特征值和奇异值
参考链接:https://blog.youkuaiyun.com/qq_36653505/article/details/82052593
特征值: 针对的是
n
n
n阶方阵。设A是n阶方阵,如果存在 λ 和n维非零向量x,使
A
x
=
λ
x
Ax=\lambda x
Ax=λx,则 λ 称为方阵A的一个特征值,x为方阵A对应于或属于特征值 λ 的一个特征向量。从定义上来看,对特征向量
x
x
x进行
A
A
A变换实质上是对
x
x
x进行缩放,缩放因子为
λ
\lambda
λ,所以
x
x
x的方向也不变。一个变换方阵的所有特征向量组成了这个变换矩阵的一组基。N个特征向量就是N个标准正交基,而特征值的模则代表矩阵在每个基上的投影长度(
∣
∣
A
∣
∣
cos
<
A
,
x
>
=
A
x
∣
∣
x
∣
∣
=
A
x
||A||\cos<A,x>=\frac{Ax}{||x||}=Ax
∣∣A∣∣cos<A,x>=∣∣x∣∣Ax=Ax)。特征值越大,说明矩阵在对应的特征向量上的方差越大,功率越大,信息量越多。特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,所有向量组内的其他的向量都可以由特征向量线性组合得到。
奇异值:
特征值及特征值分解都是针对方阵而言,但是大多数矩阵都不是方阵,奇异值相当于方阵中的特征值,奇异值分解相当于方阵中的特征值分解。此时将
A
A
A与其转置相乘
A
T
A
A^{T}A
ATA将会得到一个方阵,再求特征值。
SVD分解
MIT公开课视频:http://open.163.com/movie/2010/11/1/G/M6V0BQC4M_M6V2B5R1G.html
参考博客:https://blog.youkuaiyun.com/u010099080/article/details/68060274
SVD(singular value decompsition),描述:
输入:矩阵
D
M
×
N
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
,
x
i
∈
R
M
D_{M\times N}=(\rm \mathbf{{x}_{1},x_{2},...,x_{n}),x_{i}}\in R^{M}
DM×N=(x1,x2,...,xn),xi∈RM
D
=
∑
k
=
1
p
σ
k
u
k
v
k
T
=
U
M
×
M
Σ
M
×
N
V
N
×
N
T
D=\sum_{k=1}^{p}\sigma_{k} \rm \mathbf {u_{k} v_{k}^{T}}=U_{M\times M}\Sigma_{M\times N} V^{T}_{N\times N}
D=k=1∑pσkukvkT=UM×MΣM×NVN×NT
其中
Σ
\Sigma
Σ为对角矩阵,对角线上的值为矩阵
D
M
×
N
D_{M\times N}
DM×N特征值的平方根(eigenvalues),也就是奇异值(singular values),表示此维度的方差。
u
k
和
v
k
T
\rm \mathbf {u_{k} 和v_{k}^{T}}
uk和vkT为
σ
k
\sigma_{k}
σk对应的左奇异向量(left-singular vectors)和右奇异向量(left-singular vectors)。其中
U
和
V
U和V
U和V均为正交阵(列向量都是单位向量且两两正交(垂直))。
SVD的求解:
U
U
U的列由
A
A
T
AA^{T}
AAT 的单位化过的特征向量构成
V
V
V的列由
A
T
A
A^{T}A
ATA 的单位化过的特征向量构成
Σ
\Sigma
Σ的对角元素来源于
A
A
T
AA^{T}
AAT 和
A
T
A
A^{T}A
ATA 的平方根,从大到小排序选取
min
(
M
,
N
)
\min{(M,N)}
min(M,N)个特征值的平方根作为对角线。。
对于矩阵
D
=
[
2
4
1
3
0
0
0
0
]
D=\begin{bmatrix} 2 & 4 \\ 1 & 3 \\ 0 & 0 \\ 0 & 0 \end{bmatrix}
D=⎣⎢⎢⎡21004300⎦⎥⎥⎤,对应的SVD分解为:

python实现:
import numpy as np
A = np.array([[2, 4], [1, 3], [0, 0], [0, 0]])
print(np.linalg.svd(A))
左特征向量
U
U
U的意义:
U
U
U的每一列对应一个方向(成分),不同列对应的方向相互垂直。
将
Σ
\Sigma
Σ中的特征值从大到小排序,同时
U
(
和
V
)
U(和V)
U(和V)中的列
u
k
(
和
行
v
k
)
\rm \mathbf {u_{k} (和行v_{k})}
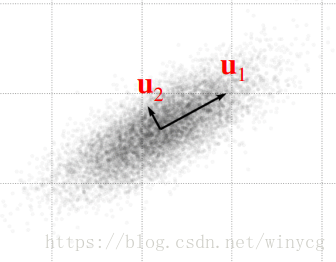
uk(和行vk)也会相应调整。其中
u
1
\rm \mathbf {u_{1}}
u1代表方差最大的方向,
u
2
\rm \mathbf {u_{2}}
u2代表与
u
1
\rm \mathbf {u_{1}}
u1垂直的方差最大的方向,
u
3
\rm \mathbf {u_{3}}
u3代表与
u
1
\rm \mathbf {u_{1}}
u1和
u
2
\rm \mathbf {u_{2}}
u2垂直的方差最大的方向。
以词项-文档关联矩阵为例,矩阵D:每一个文档由所有的M个单词进行表示,每一个维度表示此单词是否在文档中出现。
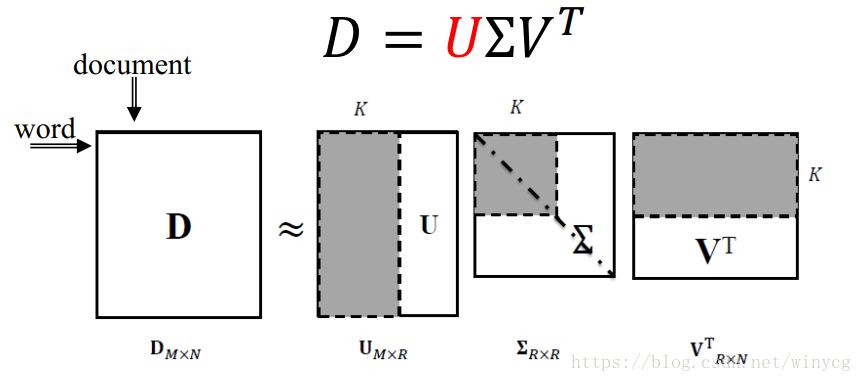
u
i
\rm \mathbf {u_{i}}
ui为M维向量,M维中的每一维表示一个单词。
u
1
,
u
2
,
.
.
.
,
u
R
\rm \mathbf {u_{1}},\rm \mathbf {u_{2}},...,\rm \mathbf {u_{R}}
u1,u2,...,uR组成了一个R维的空间,所有单词在坐标系上张成了一个空间,
u
1
\rm \mathbf {u_{1}}
u1表示方差最大的方向。
右特征向量
V
\rm \mathbf {V}
V意义:
从另一种角度看矩阵D,每一个单词可由N个文档表示,每一个维度表示是否出现该单词。
v
i
\rm \mathbf {v_{i}}
vi为N维向量,N维中的每个维度表示一个文档。
v
1
\rm \mathbf {v_{1}}
v1表示所有文档向量张成的空间中,方差最大的方向。
LSI:SVD在文本数据上的应用
LSI(latent semantic indexing)隐性语义索引,是常用的文本分析话题模型。SVD分解后的
K
K
K为话题数目。假设词项-文档矩阵为如下:
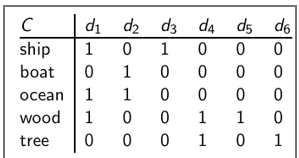
为了简单起见,采用布尔矩阵,一般可使用td-idf值。
矩阵
U
U
U:
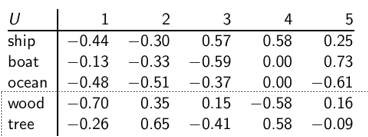
列向量给出的是不同的主题,比如政治,体育,经济等。
u
i
j
u_{ij}
uij表示词项
i
i
i和第
j
j
j个主题的相关度。
奇异值矩阵:
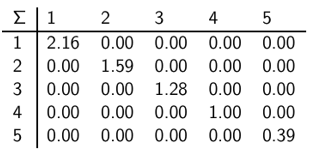
奇异值度量的是主题的重要性。可以通过舍弃较小的奇异值从而删去重要性较小的语义,达到降维的目的。
矩阵
V
V
V
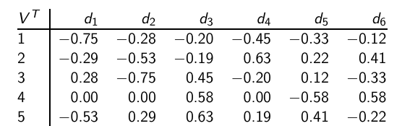
行向量给出的是不同的主题。
v
i
j
v_{ij}
vij表示文档
i
i
i和第
j
j
j个主题的相关度。
将主题压缩到2维,
C
2
=
U
Σ
2
V
T
C_{2}=U\Sigma_{2}V^{T}
C2=UΣ2VT。然后比较
C
C
C和
C
2
C_{2}
C2.
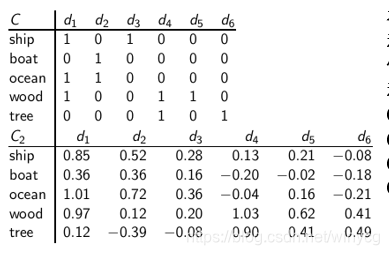
由
C
⇒
C
2
C\Rightarrow C2
C⇒C2,矩阵的秩由5变为2,所以
C
2
C_{2}
C2看作是
C
C
C的低秩近似。在原始的
C
C
C中,'boat’和‘ship’没有余弦相似度,在
C
2
C_{2}
C2中,'boat’和‘ship’具有较高的相似度。低秩近似后,重要主题信息被保留,一些枝节信息被删除。枝节信息可能是噪声,也可能是使得本来应该相似的对象不相似的细节信息。比如鲜红的花朵和红黑的花朵,把颜色信息去掉后更容易看到相似性。
优点: 数学优美,有效
缺点: 低秩矩阵和
U
U
U和
V
V
V中有负值,不好理解;特征向量两两正交,计算难度大。
NMF矩阵分解(nonnegative matrix factorization)
V
≈
W
H
T
V\approx WH^{T}
V≈WHT
其中原始矩阵
V
V
V的值非负,输出矩阵的
W
W
W和
H
H
H的值也是非负的,且不再要求是非负矩阵。求解
W
H
WH
WH的欧式距离优化目标为:
max
W
,
H
1
2
∣
∣
V
−
W
H
T
∣
∣
2
2
=
∑
i
=
1
m
∑
j
=
1
n
(
V
i
j
−
w
i
h
j
)
2
s
.
b
.
W
i
k
≥
0
,
H
k
j
≥
0
,
∀
i
,
k
,
j
\max_{W,H}\frac{1}{2}||V-WH^{T}||_{2}^{2}=\sum_{i=1}^{m}\sum_{j=1}^{n}(V_{ij}-\bm{w}_{i}\bm{h}_{j})^{2}\\ s.b. \ W_{ik}\geq0,H_{kj}\geq0, \forall i,k,j
W,Hmax21∣∣V−WHT∣∣22=i=1∑mj=1∑n(Vij−wihj)2s.b. Wik≥0,Hkj≥0,∀i,k,j
上述目标函数是非凸的,无全局最优解。有2个未知数,进行交替优化,在固定
W
W
W(或
H
H
H)后,目标函数对
H
H
H(或
W
W
W)是凸函数。所以采用如下的优化策略:(1)随机对
W
W
W赋值。(2)固定
W
W
W,最优化
H
H
H。(3)固定
H
H
H,最优化
W
W
W。(4)重复(2)(3),直至收敛。
采用梯度下降优化:
w
i
k
←
w
i
k
−
μ
i
k
∂
J
∂
w
i
k
=
w
i
k
−
μ
i
k
[
−
(
V
−
W
H
)
H
T
]
i
k
h
k
j
←
h
k
j
−
η
k
j
∂
J
∂
h
k
j
=
h
k
j
−
η
k
j
[
−
W
T
(
V
−
W
H
)
]
k
j
w_{ik}\leftarrow w_{ik}-\mu_{ik}\frac{\partial J}{\partial w_{ik}}=w_{ik}-\mu_{ik}[-(V-WH)H^{T}]_{ik} \\ h_{kj}\leftarrow h_{kj}-\eta_{kj}\frac{\partial J}{\partial h_{kj}}=h_{kj}-\eta_{kj}[-W^{T}(V-WH)]_{kj}
wik←wik−μik∂wik∂J=wik−μik[−(V−WH)HT]ikhkj←hkj−ηkj∂hkj∂J=hkj−ηkj[−WT(V−WH)]kj
直接使用梯度下降,不能保证非负,通过修改学习率将梯度下降变为乘法算法。令:
μ
i
k
=
w
i
k
[
W
H
H
T
]
i
k
,
η
k
j
=
h
k
j
[
W
T
W
H
]
k
j
\mu_{ik}=\frac{w_{ik}}{[WHH^{T}]_{ik}}, \eta_{kj}=\frac{h_{kj}}{[W^{T}WH]_{kj}}
μik=[WHHT]ikwik,ηkj=[WTWH]kjhkj
梯度下降变为乘法算法:
w
i
k
←
w
i
k
[
V
H
T
]
i
k
[
W
H
H
T
]
i
k
h
k
j
←
h
k
j
[
W
T
V
]
k
j
[
W
T
W
H
]
k
j
w_{ik}\leftarrow w_{ik}\frac{[VH^{T}]_{ik}}{[WHH^{T}]_{ik}} \\ h_{kj}\leftarrow h_{kj}\frac{[W^{T}V]_{kj}}{[W^{T}WH]_{kj}}
wik←wik[WHHT]ik[VHT]ikhkj←hkj[WTWH]kj[WTV]kj
此时每一次迭代,只要
W
W
W和
H
H
H为非负,迭代之后的
W
W
W和
H
H
H也为非负。最终得到的
W
W
W和
H
H
H为非负。
NMF用于词项-文档主题模型
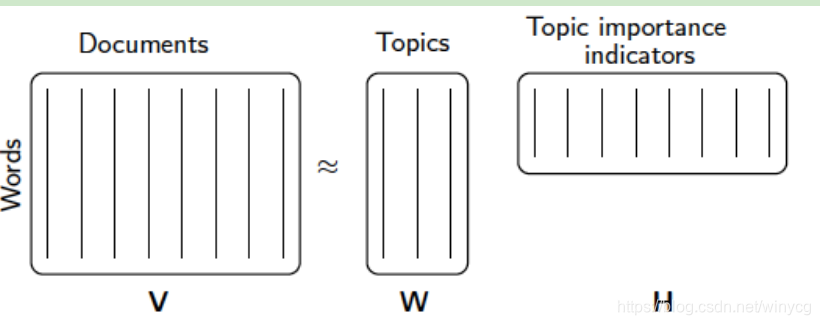
对于词项文档矩阵
V
i
×
j
V_{i\times j}
Vi×j,通常的值为td-idf。将其分解后,分别为
W
i
×
k
W_{i\times k}
Wi×k和
H
k
×
j
H_{k\times j}
Hk×j,其中
k
k
k为隐含的主题数目。
W
i
k
W_{ik}
Wik表示第
i
i
i个词与第
k
k
k个主题的相关度,
H
k
j
H_{kj}
Hkj表示第
k
k
k个主题与第
j
j
j个文档的相关度
import numpy as np
V = np.array(
[[5, 5, 3, 0, 5, 5],
[5, 0, 0, 0, 4, 4],
[0, 3, 0, 5, 4, 5],
[5, 4, 3, 3, 5, 5]])
from sklearn.decomposition import NMF
model = NMF(n_components=2)
W = model.fit_transform(V)
H = model.components_
# 利用NMF分解的结果重构V
print(W.dot(H))
[[5.80643355 3.49158155 2.43565648 0.80514285 5.16417069 5.09095253]
[4.26759859 2.19132302 1.73562676 0. 3.36296649 3.20554893]
[0.02481246 3.29247521 0.48708792 5.17675147 3.80380437 4.70921875]
[4.66621253 3.87135359 2.11231399 2.32870172 5.37938527 5.61496605]]
从 V [ 1 , 2 ] , V [ 1 , 3 ] V[1,2],V[1,3] V[1,2],V[1,3]可以看出虽然原始矩阵 V [ 1 , 2 ] , V [ 1 , 3 ] V[1,2],V[1,3] V[1,2],V[1,3]为0,但是重构的矩阵中 V [ 1 , 2 ] = 2.19 V[1,2]=2.19 V[1,2]=2.19。由此可以看出,NMF具有局部平滑的功能。在文本中,平滑指文档比较相似。
- 如果一个词在一些文档中出现,也会在其他文档出现。NMF重构之后,稀疏的词项-文档矩阵会变成稠密的矩阵。
- 原始矩阵中,词项w1在d1,d2,d3文档中出现,词项w2在d1,d2中出现,NMF重构之后,会认为词项w2在d3中也有一定概率出现。
NMF解决了SVD的计算复杂问题,且求得的所有矩阵都为正值,更好理解。两者的不同在于SVD根据奇异值的大小确定保留哪些隐含维度,NMF直接根据指定的隐含维度分解矩阵。
























 729
729

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








