K-Means聚类

聚类

聚类是无监督学习，用于寻找数据内部的分布结构。聚类将样本集D={(xi,yi)}1ND=\{(\bm{x}_{i},y_{i})\}_{1}^{N}D={(xi​,yi​)}1N​划分为$k$个互不相交的子集{Cm}1M\{C_{m}\}_{1}^{M}{Cm​}1M​，即样本簇。

K-Means

给定样本集D={x1,x2,...,xm}D=\{x_{1},x_{2},...,x_{m}\}D={x1​,x2​,...,xm​},k均值算法针对聚类所得到的簇划分C={C1,C2,...,Ck}C=\{C_{1},C_{2},...,C_{k}\}C={C1​,C2​,...,Ck​}最小化平方误差（SSE，sum of squared error），也称簇惯性（cluster interia）：$$SSE=\sum _{i=1}^k\sum _{x\in c_i}{\Vert x-{\mu }_i\Vert }^2$$
其中${\mu }_i=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$是簇$C_i$的均值向量。上述刻画了簇内样本围绕均指向量的紧密程度，E值越小簇内样本相似性越高。但是该式最小化需要考虑样本集所有的簇划分，是一个NP难问题。K值作为超参数需要用户指定。
算法流程：
输入：训练集D={x1,x2,...,xm}D=\{x_{1},x_{2},...,x_{m}\}D={x1​,x2​,...,xm​}和聚类簇数$k$
1.从$D$中随机选择$k$个样本作为均值向量{μ1,μ2,...,μk}\{\mu_{1},\mu_{2},...,\mu_{k}\}{μ1​,μ2​,...,μk​}
2. repeat
3. --------$forj=1,2,...,mdo$
4. ----------------计算样本$x_j$与各均值向量${\mu }_i,i=1,2,...,k$的距离：$d_{ji}=\Vert x_j-{\mu }_i\Vert$
5. ----------------根据距离最近的均值向量确定$x_j$的簇标记arg⁡min⁡i∈{1,2,...,k}dji\arg \min_{i\in \{1,2,...,k\}}d_{ji}argmini∈{1,2,...,k}​dji​
6. --------$endfor$
7. --------$fori=1,2,...,kdo$
8. ----------------更新均值向量${\mu }_i=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$
9. until当前均值向量均未更新。（通常可设置最大运行轮数或最小调整幅度阈值）

算法的优点：
1.简单，易于理解和实现
2.高效，时间复杂度为$O(TKM)$,T为运行轮数，K簇数，M样本数
缺点：
1.局部最优解。每一个数据点贪心选择距离最近的点，不同出市中心簇的结果可能不同。
2.平均值点的概念对类别特征不适应。
3.K值难以预知
4.对离群点（outlier）比较敏感，因为是求平均值点，所以存在较远异常点的情况下可能造成中心点偏离密集点。

from sklearn.datasets import make_blobs
# 聚类数据生成器
X, y = make_blobs(n_samples=150,
                  n_features=2,
                  centers=3,
                  cluster_std=0.5,
                  shuffle=True,
                  random_state=0)
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3,  # 设定簇数k=3
            init='random',  # 表示使用kmeans算法
            n_init=10,  # 基于不同随机初始点run10次，并选择SSE最小的最终模型
            max_iter=300,  # 最大迭代次数
            tol=1e-4,  # SSE的容忍度
            random_state=0)
y_km = km.fit_predict(X)

import matplotlib.pyplot as plt
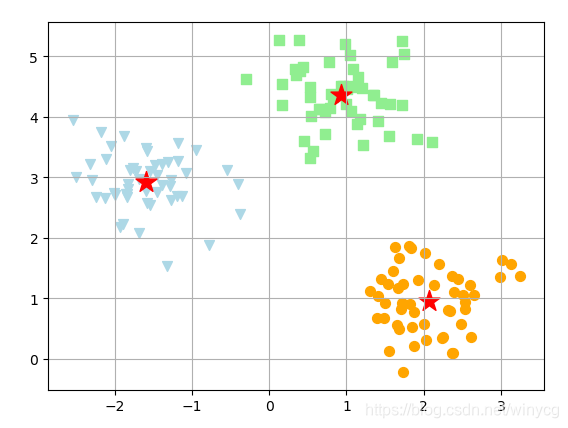
plt.scatter(X[y_km == 0, 0], X[y_km == 0, 1], s=50, c='lightgreen', marker='s', label='cluster1')
plt.scatter(X[y_km == 1, 0], X[y_km == 1, 1], s=50, c='orange', marker='o', label='cluster2')
plt.scatter(X[y_km == 2, 0], X[y_km == 2, 1], s=50, c='lightblue', marker='v', label='cluster3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
            s=250, c='red', marker='*', label='center')
plt.grid()
plt.show()

K-Means的改进
普通的K-means算法每次在批量的划分完样本之后再修正类心，这种粗粒度的修正使得并不能得到最好的收敛目标（最小化误差平方和），且在划分样本时可能出现空簇。为了解决上述问题，进行细粒度的划分样本，每划分一次样本直接进行类心的修正，此方法能保证收敛到确定的误差。
若某样本$\mathbf{x}$从簇$C_i$移到簇$C_k$，此时对两个簇均方误差的变化为：
$$\begin{gathered} J_i=J_i-\frac{N_i}{N_i-1}||\mathbf{x}-m_i|{|}^2 \\ {J}_k=J_k+\frac{N_k}{N_k-1}||\mathbf{x}-m_k|{|}^2 \end{gathered}$$
其中$N_i$和$N_k$分别是簇$C_i$和簇$C_k$的样本数
算法过程如下：
首先采用和朴素K-means相同的初始化生成一个初始聚类结果。
（1）如果$N_i=1$，则放弃该样本的移动判断，该步保证了不会有空簇的出现。
（2）计算与各簇$C_j$的相似度：
$${\rho }_j=\{\begin{array}{c}\frac{N_i}{N_i-1}||\mathbf{x}-{\mathbf{m}}_i|{|}^2,j=i\\ \frac{N_j}{N_j+1}||\mathbf{x}-{\mathbf{m}}_j|{|}^2,j̸=i\end{array}$$
选择移入的簇$C_k$的$k$为：
$$k^{\ast }=\underset{k}{\min }{\rho }_k$$
这实质为：如果最小值为${\rho }_i$，表明此时不要移动样本，移动会导致总体的均平方误差增大。若不是${\rho }_i$，移动会使得总体的均平方误差减小。
（3）修正被调整的两个类的类心：
$$\begin{gathered} {\mathbf{m}}_i={\mathbf{m}}_i-\frac{\mathbf{x}-{\mathbf{m}}_i}{N_i-1} \\ {\mathbf{m}}_k={\mathbf{m}}_k+\frac{\mathbf{x}-{\mathbf{m}}_k}{N_k-1} \end{gathered}$$
（4）计算两个簇的误差：
$$\begin{gathered} J_i=J_i-\frac{N_i}{N_i-1}||\mathbf{x}-m_i|{|}^2 \\ {J}_k=J_k+\frac{N_k}{N_k-1}||\mathbf{x}-m_k|{|}^2 \end{gathered}$$
若经过全部样本遍历后，各簇的误差保持不变，表明此时算法收敛。