线性SVM
SVM的优化目标是最大化分类边距,边距是指两个分离的超平面(决策边界)间的距离,位于分类边距上的数据点成为支持向量。图中蓝线所指的就是支持向量。
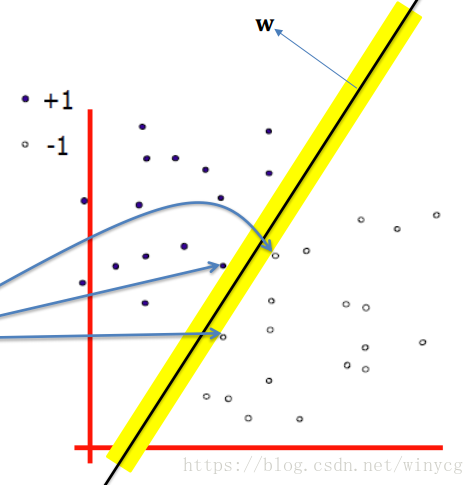
计算边距的大小:
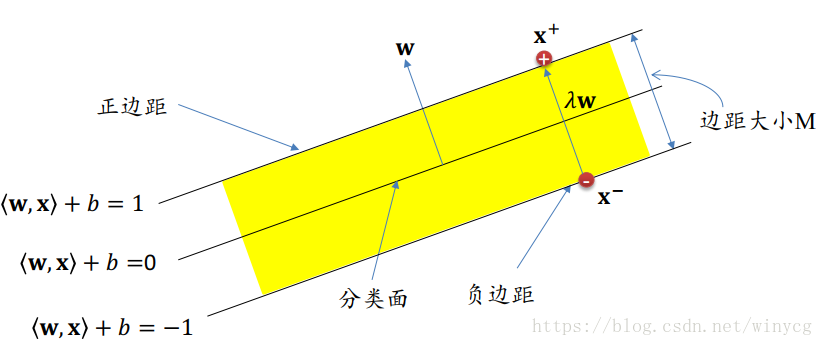
设分类的超平面为:
g(x)=wTx+b=0g(\bm{x})=\bm{w}^{T}\bm{x}+b=0g(x)=wTx+b=0
支撑超平面为g(x)=±cg(\bm{x})=\pm cg(x)=±c,令c=1c=1c=1:
{wTxi+b⩾1,yi=+1wTxi+b⩽−1,yi=−1\left\{\begin{matrix}
\bm{w}^{T}\bm{x}_{i}+b\geqslant1,y_{i}=+1\\
\bm{w}^{T}\bm{x}_{i}+b\leqslant-1,y_{i}=-1
\end{matrix}\right.{wTxi+b⩾1,yi=+1wTxi+b⩽−1,yi=−1
虽然在这里假设c=1c=1c=1,所求得的(w,b)(\bm{w},b)(w,b)若能正确分类,总存在缩放变换: w→ζw,b→ζb\bm{w} \rightarrow \zeta\bm{w},\bm{b} \rightarrow \zeta\bm{b}w→ζw,b→ζb使得上式成立。
由样本到超平面的距离公式:
d=∣g(x)∣∣∣w∣∣d=\frac{|g(\bm{x})|}{||\bm{w}||}d=∣∣w∣∣∣g(x)∣
分类间隔为:
∣+1∣∣∣w∣∣+∣−1∣∣∣w∣∣=2∣∣w∣∣\frac{|+1|}{||\bm{w}||}+\frac{|-1|}{||\bm{w}||}=\frac{2}{||\bm{w}||}∣∣w∣∣∣+1∣+∣∣w∣∣∣−1∣=∣∣w∣∣2
SVM的学习过程归结为寻找合适的w{\rm{w}}w和bbb:
- 所有的训练数据都在正确的分类区域
yi(⟨w,xi⟩+b)≥1,其中yi∈{−1,+1}y_{i}(\left \langle {\rm{w}},{\rm{x}}_{i} \right \rangle+b) \geq 1,其中y_{i} \in \{-1, +1\}yi(⟨w,xi⟩+b)≥1,其中yi∈{−1,+1} - 最大化边距:max2∥w∥⇔min12∥w∥2\max \frac{2}{\parallel {\bm{w}}\parallel} \Leftrightarrow\min \frac{1}{2}{\parallel {\bm{w}}\parallel}^{2}max∥w∥2⇔min21∥w∥2
目标函数可以被整理成为如下的格式:
minw,b12∣∣w∣∣2s.t. yi(wTxi+b)≥1,i=1,2,...,n\min_{\bm{w},b}\frac{1}{2}||\mathbf{\bm{w}}||^{2} \\ s.t. \ y_{i}(\bm{{w}^{T}x_{i}}+b)\geq1,i=1,2,...,nw,bmin21∣∣w∣∣2s.t. yi(wTxi+b)≥1,i=1,2,...,n
此时可以使用在约束g(x)≤0g(\bm{x})\leq0g(x)≤0下最小化f(x)f(\bm{x})f(x)的拉格朗日乘数法,此时需要转化为如下的KKT约束条件:
{g(x)⩽0λ⩾0λg(x)=0 \left\{\begin{matrix} g(\bm{x})\leqslant 0\\ \lambda\geqslant0\\ \lambda g(\bm{x})=0 \end{matrix}\right.⎩⎨⎧g(x)⩽0λ⩾0λg(x)=0
每条约束添加拉格朗日乘子αi⩾0\alpha_{i}\geqslant0αi⩾0,该问题的拉格朗日函数可写为:L(w,b,α)=12∣∣w∣∣2+∑i=1nαi(1−yi(wTxi+b))L(\bm{w},b,\bm{\alpha})=\frac{1}{2}||\mathbf{\bm{w}}||^{2}+\sum_{i=1}^{n}\alpha_{i}(1-y_{i}(\bm{{w}^{T}x_{i}}+b))L(w,b,α)=21∣∣w∣∣2+i=1∑nαi(1−yi(wTxi+b))
原始问题:minw,bθp(w,b)=minw,bmaxαi⩾0L(w,b,α)=p∗\min_{\bm{w},b}\theta_{p}(\bm{w},b)=\min_{\bm{w},b} \max_{\alpha_{i}\geqslant 0}L(\bm{w},b,\alpha)=p^{*}minw,bθp(w,b)=minw,bmaxαi⩾0L(w,b,α)=p∗
对偶问题:maxαθd(α)=maxαi⩾0minw,bL(w,b,α)=d∗\max_{\alpha}\theta_{d}(\alpha)=\max_{\alpha_{i}\geqslant 0}\min_{\bm{w},b}L(\bm{w},b,\alpha)=d^{*}maxαθd(α)=maxαi⩾0minw,bL(w,b,α)=d∗
从以上可以看出,原始问题先固定α\alphaα优化w,b\bm{w},bw,b,求出w,b\bm{w},bw,b再优化α\alphaα。对偶问题先固定w,b\bm{w},bw,b优化α\alphaα,求出α\alphaα后在优化w,b\bm{w},bw,b。采用其对偶问题,先固定先固定w,b\bm{w},bw,b:
∂L(w,b,α)∂w=0⇒w=∑i=1nαiyixi∂L(w,b,α)∂b=0⇒0=∑i=1nαiyi\frac{\partial{L(\bm{w},b,\bm{\alpha})}}{\partial{\bm{w}}}=0\Rightarrow\bm{w}=\sum_{i=1}^{n}\alpha_{i}y_{i}\bm{x}_{i} \\ \frac{\partial{L(\bm{w},b,\bm{\alpha})}}{\partial{b}}=0\Rightarrow 0=\sum_{i=1}^{n}\alpha_{i}y_{i}∂w∂L(w,b,α)=0⇒w=i=1∑nαiyixi∂b∂L(w,b,α)=0⇒0=i=1∑nαiyi
将以上两式子带入L(w,b,α)L(\bm{w},b,\bm{\alpha})L(w,b,α)可得:
12∣∣w∣∣2=12∑i=1n∑j=1nαiαjyiyjxiTxj−∑i=1nαi(1−yi(wTxi+b))=−∑i=1n∑j=1nαiαjyiyjxiTxj+∑i=1nαi\frac{1}{2}||\bm{w}||^{2}=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}\\ -\sum_{i=1}^{n}\alpha_{i}(1-y_{i}(\bm{{w}^{T}x_{i}}+b))=-\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}+\sum_{i=1}^{n}\alpha_{i}21∣∣w∣∣2=21i=1∑nj=1∑nαiαjyiyjxiTxj−i=1∑nαi(1−yi(wTxi+b))=−i=1∑nj=1∑nαiαjyiyjxiTxj+i=1∑nαi
得到θd(α)=∑i=1nαi−12∑i=1n∑j=1nαiαjyiyjxiTxj\theta_{d}(\alpha)=\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}θd(α)=∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjxiTxj
此时需要求解如下关于α\alphaα目标函数:
maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyjxiTxjs.t. ∑i=1nαiyi=0,αi⩾0,i=1,2,...,n\max_{\alpha}\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}\\ s.t. \ \sum_{i=1}^{n}\alpha_{i}y_{i}=0, \\ \alpha_{i}\geqslant0,i=1,2,...,nαmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjxiTxjs.t. i=1∑nαiyi=0,αi⩾0,i=1,2,...,n
上述过程需满足KKT条件:
{yif(xi)−1⩾0αi⩾0αi(yif(xi)−1)=0\left\{\begin{matrix} y_{i}f(\bm{x}_{i})-1\geqslant 0\\ \alpha_{i} \geqslant 0\\ \alpha_{i}(y_{i}f(\bm{x}_{i})-1)=0 \end{matrix}\right.⎩⎨⎧yif(xi)−1⩾0αi⩾0αi(yif(xi)−1)=0
从KKT条件中可以看出,对于∀(xi,yi)\forall (\bm{x}_{i},y_{i})∀(xi,yi),必有αi=0\alpha_{i}=0αi=0或yif(xi)=1y_{i}f(\bm{x}_{i})=1yif(xi)=1。当样本点为非支持向量时,αi=0\alpha_{i}=0αi=0,样本对f(x)f(\bm{x})f(x)没有影响,当αi>0\alpha_{i}>0αi>0时,必有yif(xi)=1y_{i}f(\bm{x}_{i})=1yif(xi)=1,此时对应的样本点为支持向量。所以最终的模型只和支持向量有关。
解出α\alphaα后,求出w,b\bm{w},bw,b:
w=∑i=1nαiyixi=∑xi∈SVαiyixiyj(wTxj+b)−1=0{j∣αj>0}⇒b=yj−wTxj\bm{w}=\sum_{i=1}^{n}\alpha_{i}y_{i}\bm{x}_{i} =\sum_{\bm{x}_{i}\in SV}\alpha_{i}y_{i}\bm{x}_{i} \\ y_{j}(\bm{w}^{T}\bm{x}_{j}+b)-1=0 \{j|\alpha_{j}>0\}\\ \Rightarrow b=y_{j}- \bm{w}^{T}\bm{x}_{j}w=i=1∑nαiyixi=xi∈SV∑αiyixiyj(wTxj+b)−1=0{j∣αj>0}⇒b=yj−wTxj
理论上偏置项bbb的确定可以根据任意的支持向量求解,在现实任务中,采用更加鲁棒性的做法:使用所有支持向量的平均值:
b=1∣SV∣∑xi∈SV(yi−wTxi)b=\frac{1}{|SV|}\sum_{\bm{x}_{i}\in SV}(y_{i}- \bm{w}^{T}\bm{x}_{i})b=∣SV∣1xi∈SV∑(yi−wTxi)
即可得到模型:
f(x)=wTx+b=∑i=1nαiyixiTx+1∣SV∣∑xi∈SV(yi−wTxi)f(\bm{x})=\bm{w}^{T}\bm{x}+b \\ =\sum_{i=1}^{n}\alpha_{i}y_{i}\bm{x}_{i}^{T}\bm{x}+\frac{1}{|SV|}\sum_{\bm{x}_{i}\in SV}(y_{i}- \bm{w}^{T}\bm{x}_{i})f(x)=wTx+b=i=1∑nαiyixiTx+∣SV∣1xi∈SV∑(yi−wTxi)
非线性SVM:核函数法
可将样本映射到高维空间中,使得在低维空间线性不可分的样本在高维空间线性可分。
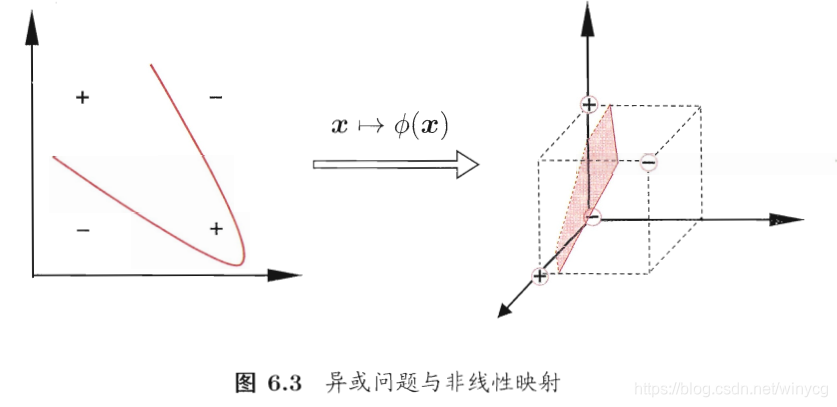
设ϕ(x)\phi(\bm{x})ϕ(x)为x\bm{x}x映射后的特征向量,在特征空间中划分超平面的模型为f(x)=wTϕ(x)+bf(\bm{x})=\bm{w}^{T}\phi(\bm{x})+bf(x)=wTϕ(x)+b
此时的对偶问题是:
maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyjϕ(xi)Tϕ(xj)s.t. ∑i=1nαiyi=0,αi⩾0,i=1,2,...,n\max_{\alpha}\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}\phi(x_{i})^{T}\phi(x_{j})\\
s.t. \ \sum_{i=1}^{n}\alpha_{i}y_{i}=0, \\
\alpha_{i}\geqslant0,i=1,2,...,nαmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjϕ(xi)Tϕ(xj)s.t. i=1∑nαiyi=0,αi⩾0,i=1,2,...,n
由于特征空间可能维度很高,甚至是无穷维,内积运算ϕ(xi)Tϕ(xj)\phi(x_{i})^{T}\phi(x_{j})ϕ(xi)Tϕ(xj)比较困难。此时可以设想一个核函数:
κ(xi,xj)=ϕ(xi)Tϕ(xj)\kappa(\bm{x_{i},x_{j}})=\phi(\bm{x_{i}})^{T}\phi(\bm{x}_{j})κ(xi,xj)=ϕ(xi)Tϕ(xj)
有了核函数,就无需再求高维甚至无穷维特征空间的内积,目标函数可写为:
maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyjκ(xi,xj)s.t. ∑i=1nαiyi=0,αi⩾0,i=1,2,...,n\max_{\alpha}\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}\kappa(\bm{x_{i},x_{j}})\\
s.t. \ \sum_{i=1}^{n}\alpha_{i}y_{i}=0, \\
\alpha_{i}\geqslant0,i=1,2,...,nαmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjκ(xi,xj)s.t. i=1∑nαiyi=0,αi⩾0,i=1,2,...,n
解出α\alphaα后,求出w,b\bm{w},bw,b:
w=∑i=1nαiyixiyi(wTxi+b)−1=0{i∣αi>0}⇒b=yj−∑i=1nαiyiκ(xi,xj)\bm{w}=\sum_{i=1}^{n}\alpha_{i}y_{i}\bm{x}_{i} \\
y_{i}(\bm{w}^{T}\bm{x}_{i}+b)-1=0 \{i|\alpha_{i}>0\}\\
\Rightarrow b=y_{j}-\sum_{i=1}^{n}\alpha_{i}y_{i}\kappa(x_{i},x_{j})w=i=1∑nαiyixiyi(wTxi+b)−1=0{i∣αi>0}⇒b=yj−i=1∑nαiyiκ(xi,xj)
f(x)=wTx+b=∑i=1nαiyiϕ(xi)Tϕ(x)+b=∑i=1nαiyiκ(xi,x)+bf(\bm{x})=\bm{w}^{T}\bm{x}+b=\sum_{i=1}^{n}\alpha_{i}y_{i}\phi(\bm{x}_{i})^{T}\phi(\bm{x})+b=\sum_{i=1}^{n}\alpha_{i}y_{i}\kappa(\bm{x_{i},x})+bf(x)=wTx+b=i=1∑nαiyiϕ(xi)Tϕ(x)+b=i=1∑nαiyiκ(xi,x)+b
核函数:
若已知合适的映射ϕ(⋅)\phi(\cdot )ϕ(⋅),则可写出核函数κ(⋅)\kappa(\cdot )κ(⋅)。在现实任务中我们通常不知道ϕ(⋅)\phi(\cdot )ϕ(⋅)的形式,我们有以下定理可以选择核函数。
X\mathcal{X}X为输入空间,κ(⋅,⋅)\kappa(\cdot,\cdot )κ(⋅,⋅)是定义在X×X\mathcal{X}\times \mathcal{X}X×X的对称函数,则κ\kappaκ是核函数当且仅当对于任意数据D={x1,x2,...,xm}D=\{\bm{x}_{1},\bm{x}_{2},...,\bm{x}_{m}\}D={x1,x2,...,xm},核矩阵K\mathbf{K}K总是半正定的。
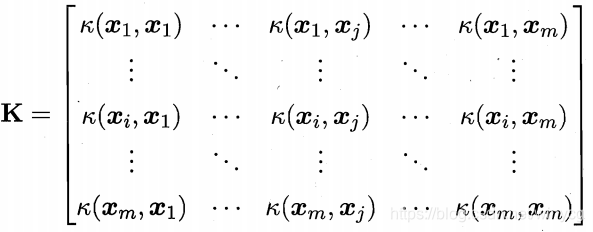
矩阵正定的定义: 对于实对称矩阵AAA,如果对于任意的非0向量x∈Rn≠0\bm{x}\in R^{n}\neq 0x∈Rn̸=0,有xTAx>0\bm{x}^{T}A\bm{x}>0xTAx>0,则矩阵AAA是正定的。其充要条件是矩阵AAA对应的特征值全是正数。
上述的定理表明,对于任意一个对称函数所对应的核矩阵半正定,就能作为核函数使用,同时也隐式对应映射函数ϕ\phiϕ。
我们希望样本在特征空间里线性可分,特征空间的好坏对SVM的性能很重要。在不知道特征映射的情况下,我们并不知道什么样的核函数是最适合的,核函数隐式的定义了特征空间。于是核函数的选择成为SVM的最大变数。若核函数选择不合适,样本会映射到一个不合适的空间,进而导致性能不佳。
常用的核函数:

新的核函数也可以通过组合核函数得到:
- 若κ1\kappa_{1}κ1和κ2\kappa_{2}κ2为核函数,对于任意正数γ1\gamma_{1}γ1和γ2\gamma_{2}γ2,其线性组合γ1κ1+γ2κ2\gamma_{1}\kappa_{1}+\gamma_{2}\kappa_{2}γ1κ1+γ2κ2也是核函数。
- 若κ1\kappa_{1}κ1和κ2\kappa_{2}κ2为核函数,则核函数的直积(笛卡尔积)κ1(x,z)κ2(x,z)\kappa_{1}(\bm{x,z})\kappa_{2}(\bm{x,z})κ1(x,z)κ2(x,z)也是核函数。
- 若κ1\kappa_{1}κ1为核函数,则对于任意函数g(x)g(\bm{x})g(x) $κ(x,z)=g(x)κ1(x,z)g(z)\kappa(\bm{x,z})=g(\bm{x})\kappa_{1}(\bm{x,z})g(\bm{z})κ(x,z)=g(x)κ1(x,z)g(z)
软边距的SVM
如果不存在一个分类面使得训练数据能够被完美分开,或者为了防止由于过拟合而造成的线性可分,那么边距不再是硬性限制(软边距),此时允许一些样本分类错误。这些样本不必满足:
yi(wTxi+b)≥1y_{i}(\bm{w}^{T}\bm{x}_{i}+b)\geq 1yi(wTxi+b)≥1
此时需要在优化目标中加入对错误样本的惩罚,错误惩罚为出错数据点与分类面的距离。如果不加入惩罚项,支持向量会变为最外侧的样本点,造成分类失败;加入惩罚项,会在最大边距与错误样本惩罚项之间得到权衡。
优化目标:minw,b,ξi12∣∣w∣∣2+C∑i=1nξis.t. yi(wTxi+b)≥1−ξiξi≥0,i=1,2,...,n\min_{\bm{w},b,\xi_{i}} {\frac{1}{2}||{\bm{w}}||}^{2}+C\sum_{i=1}^{n}\xi_{i} \\
s.t. \ y_{i}(\bm{w}^{T}\bm{x}_{i}+b)\geq 1-\xi_{i} \\
\xi_{i}\geq 0,i=1,2,...,nw,b,ξimin21∣∣w∣∣2+Ci=1∑nξis.t. yi(wTxi+b)≥1−ξiξi≥0,i=1,2,...,n
例如可以使用hinge函数:l(z)=max(0,1−z)l(z)=\max(0,1-z)l(z)=max(0,1−z)
此时优化函数可写为:
minw,b,ξi12∣∣w∣∣2+C∑i=1nmax(0,1−yi(wTxi+b))\min_{\bm{w},b,\xi_{i}} {\frac{1}{2}||{\bm{w}}||}^{2}+C\sum_{i=1}^{n}\max(0,1-y_{i}(\bm{w}^{T}\bm{x}_{i}+b))w,b,ξimin21∣∣w∣∣2+Ci=1∑nmax(0,1−yi(wTxi+b))
其中参数CCC是一个权衡,CCC变大,牺牲了分类间隔,减少了训练集错误。
对偶问题为:
目标函数可写为:
maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyjκ(xi,xj)s.t. ∑i=1nαiyi=0,0≤αi≤C,i=1,2,...,n\max_{\alpha}\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}\kappa(\bm{x_{i},x_{j}})\\
s.t. \ \sum_{i=1}^{n}\alpha_{i}y_{i}=0, \\
0\leq \alpha_{i} \leq C,i=1,2,...,nαmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjκ(xi,xj)s.t. i=1∑nαiyi=0,0≤αi≤C,i=1,2,...,n
可以看出,与软间隔的目标函数相比,变化只有增加了αi≤C\alpha_{i} \leq Cαi≤C。
f(x)=wTx+b=∑i=1nαiyiϕ(xi)Tϕ(x)+b=∑i=1nαiyiκ(xi,x)+bf(\bm{x})=\bm{w}^{T}\bm{x}+b=\sum_{i=1}^{n}\alpha_{i}y_{i}\phi(\bm{x}_{i})^{T}\phi(\bm{x})+b=\sum_{i=1}^{n}\alpha_{i}y_{i}\kappa(\bm{x_{i},x})+bf(x)=wTx+b=i=1∑nαiyiϕ(xi)Tϕ(x)+b=i=1∑nαiyiκ(xi,x)+b
利用线性SVM对鸢尾花数据集进行分类:
from sklearn.svm import SVC
import numpy as np
from sklearn.preprocessing import StandardScaler
# 数据获取和绘图函数见决策树部分:https://blog.youkuaiyun.com/winycg/article/details/82763334
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
svm = SVC(kernel='linear', C=1.0, random_state=0)
svm.fit(X_train_std, y_train)
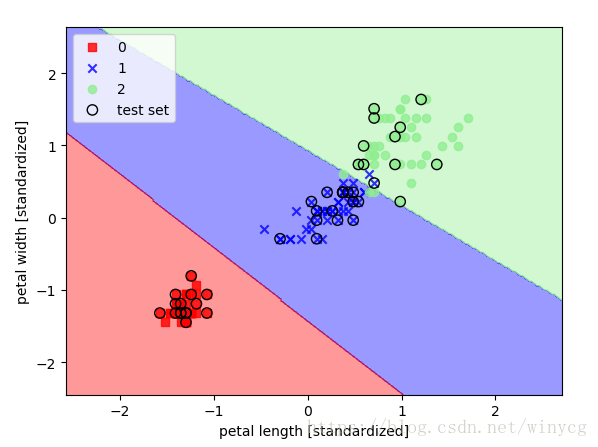





 本文深入探讨线性SVM的工作原理,包括优化目标、边距计算、拉格朗日乘数法的应用,以及如何通过核函数处理非线性问题。同时,介绍了软边距SVM的概念,用于处理不可完全线性分类的数据。
本文深入探讨线性SVM的工作原理,包括优化目标、边距计算、拉格朗日乘数法的应用,以及如何通过核函数处理非线性问题。同时,介绍了软边距SVM的概念,用于处理不可完全线性分类的数据。
















 1148
1148

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








