【AI深究】支持向量机（SVM, Support Vector Machine）全网最详细全流程详解与案例（附Python代码演示）|SVM、SVR|分类、回归任务流程|优、缺点|例子案例及数据演示

最新推荐文章于 2025-09-19 18:04:55 发布

原创最新推荐文章于 2025-09-19 18:04:55 发布 · 3.1k 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #支持向量机 #python #分类 #回归 #svm #算法

【AI深究】专栏系列专栏收录该内容

36 篇文章

订阅专栏

该文章已生成可运行项目，

大家好，我是爱酱。继前几篇系统讲解了集成方法、GMM、DBSCAN等主流算法，这一篇我们来聊聊机器学习中极为经典且实用的模型——支持向量机（SVM）。SVM不仅能做分类，还能做回归、异常检测等任务。本文将围绕SVM的核心原理、数学公式、不同用途（分类/回归）、常见核函数、实际案例与代码实现等，详细分步骤讲解，便于你直接用于技术文档和学习。

注：本文章含大量数学算式、详细例子说明及代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

一、SVM简介与应用场景

支持向量机（SVM）是一种基于统计学习理论的监督学习模型，最初用于二分类问题，但已广泛应用于多分类、回归、异常检测等场景。其核心思想是：在特征空间中寻找一个最优超平面，将不同类别的样本分开，并最大化类别间的间隔（margin）。

典型应用

文本/垃圾邮件分类
图像识别与人脸检测
基因/蛋白质分类、生物信息学
手写数字识别
金融风控、异常检测
回归预测（SVR）

二、SVM分类的数学原理

1. 线性可分SVM

对于线性可分数据，SVM目标是在特征空间中找到一个最优超平面（optimal separating hyperplane） $w^T x + b = 0$ ，使得两类样本间隔最大。

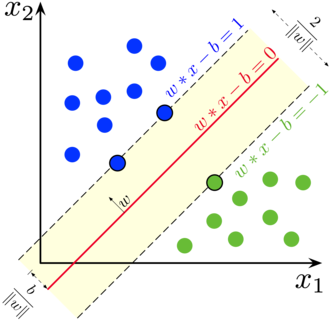
决策函数：

最优间隔的数学表达：

约束条件：

支持向量：距离超平面最近的样本点，决定了分类边界的位置。

2. 软间隔与正则化

实际数据往往不可完全线性分割，引入松弛变量 $\xi_i$ 和正则化参数 $C$ ，允许部分样本被误分：

约束：

$C$ 控制间隔最大化与误分类惩罚的权衡。

3. 非线性SVM与核方法

当数据线性不可分时，SVM通过核函数（Kernel Trick）将数据映射到高维空间，使其线性可分。

常见核函数：

线性核：
多项式核：
高斯径向基核（RBF）：

核方法让SVM能处理复杂的非线性分类问题。

4. SVM分类的对偶问题与支持向量

SVM最终可转化为对偶问题，只有支持向量（即 $\alpha_i > 0$ 的样本）参与决策：

约束：

最终分类函数：

三、SVM回归（SVR, Support Vector Regression）原理

SVM不仅能做分类，还能做回归（SVR）。其目标是找到一个对大多数样本误差在$\epsilon$范围内的回归函数。

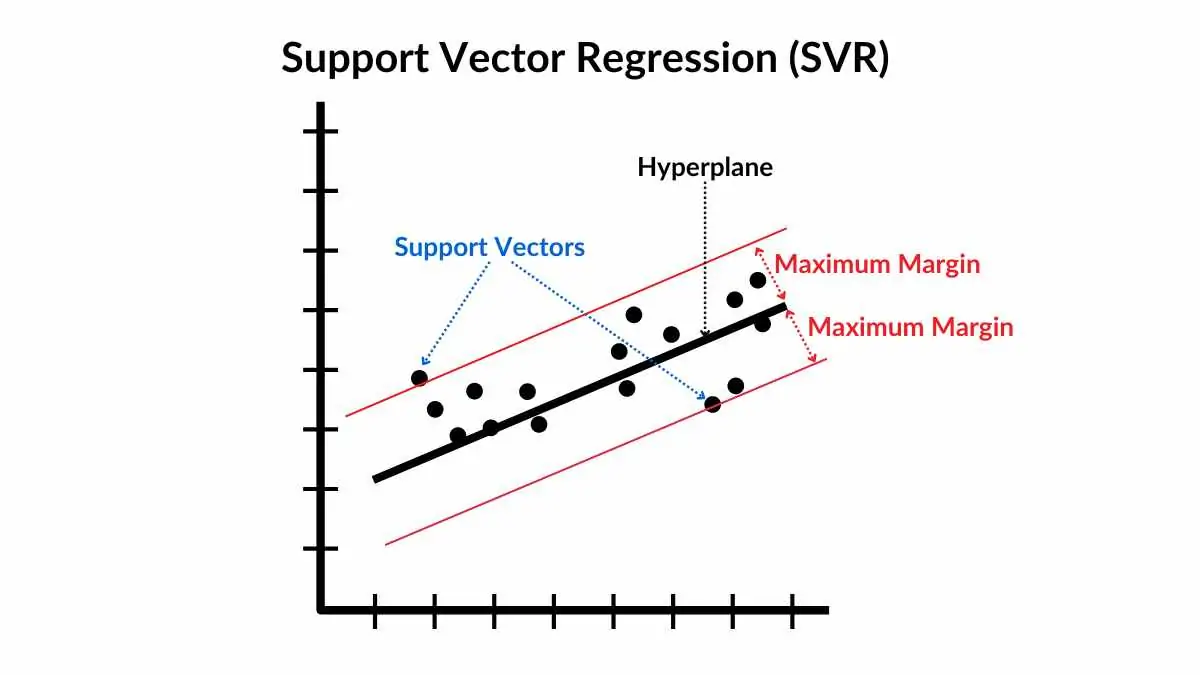
SVR优化目标：

约束：

SVR同样可结合核函数实现非线性回归。

四、SVM分类案例流程（手动二维数据）

1. 构造数据

假设我们有如下二维点：

点	$x_1$	$x_2$	类别
A	2	3	1
B	3	3	1
C	2	2	1
D	7	8	-1
E	8	8	-1
F	7	7	-1

类别1用红色，类别-1用蓝色。

2. 可视化原始数据

用散点图画出这6个点，不同类别不同颜色。
你会看到两组点在二维空间中分布明显。

3. SVM训练流程

目标：找到一条直线（超平面）将两类点分开，并让两类点距离这条线的“间隔”最大。
SVM自动确定这条线的位置和方向。
训练后，距离分界线最近的点就是“支持向量（Support Vector）”，它们决定了分类边界。

4. 结果与决策边界

SVM会输出决策边界（分界线），并标出支持向量。
你可以用网格点可视化SVM的分界线和每个点的分类区域。

五、SVR回归案例流程（手动一维数据）

1. 构造数据

假设我们有如下回归样本：

$x$	$y$
-2	-1.1
-1	-0.8
0	0.1
1	0.9
2	1.2

2. 可视化原始数据

用散点图画出$x$与$y$的关系。

3. SVR训练流程

目标：找到一条曲线或直线，使得大部分点落在“$\epsilon$带宽”内（即误差在$\epsilon$以内）。
带宽外的点会产生惩罚，模型会平衡拟合度和间隔宽度。
支持向量是那些正好落在$\epsilon$带宽边界上的点。

4. 结果与回归曲线

SVR会输出拟合曲线和$\epsilon$带宽（上下两条虚线）。
可视化时，回归曲线穿过数据点，大部分点在带宽内，极少数点在带宽外。

六、完整Python代码实现（含数据、SVM及SVR示例）

注：记得要先 pip install scikit-learn Library喔～还有请大家复制并在本地执行喔～

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC, SVR

# SVM分类案例
X_cls = np.array([[2,3],[3,3],[2,2],[7,8],[8,8],[7,7]])
y_cls = np.array([1,1,1,-1,-1,-1])

plt.figure(figsize=(6,5))
plt.scatter(X_cls[y_cls==1,0], X_cls[y_cls==1,1], color='red', label='Class 1')
plt.scatter(X_cls[y_cls==-1,0], X_cls[y_cls==-1,1], color='blue', label='Class -1')
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('Raw Data (SVM Classification)')
plt.legend()
plt.show()

# 训练SVM
clf = SVC(kernel='linear', C=100)
clf.fit(X_cls, y_cls)

# 可视化决策边界
w = clf.coef_[0]
b = clf.intercept_[0]
xx = np.linspace(1, 9, 100)
yy = -(w[0]*xx + b)/w[1]
plt.figure(figsize=(6,5))
plt.scatter(X_cls[y_cls==1,0], X_cls[y_cls==1,1], color='red', label='Class 1')
plt.scatter(X_cls[y_cls==-1,0], X_cls[y_cls==-1,1], color='blue', label='Class -1')
plt.plot(xx, yy, 'k-', label='Decision Boundary')
plt.scatter(clf.support_vectors_[:,0], clf.support_vectors_[:,1], s=120, facecolors='none', edgecolors='k', linewidths=1.5, label='Support Vectors')
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('SVM Decision Boundary & Support Vectors')
plt.legend()
plt.show()

# SVR回归案例
X_reg = np.array([[-2],[-1],[0],[1],[2]])
y_reg = np.array([-1.1, -0.8, 0.1, 0.9, 1.2])

plt.scatter(X_reg, y_reg, color='blue', label='Data')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Raw Data (SVR Regression)')
plt.legend()
plt.show()

# 训练SVR
svr = SVR(kernel='linear', C=10, epsilon=0.1)
svr.fit(X_reg, y_reg)
X_plot = np.linspace(-2.5, 2.5, 100).reshape(-1,1)
y_pred = svr.predict(X_plot)

plt.scatter(X_reg, y_reg, color='blue', label='Data')
plt.plot(X_plot, y_pred, color='red', label='SVR Prediction')
plt.xlabel('x')
plt.ylabel('y')
plt.title('SVR Regression with Epsilon-Tube')
# 画出epsilon带宽
plt.plot(X_plot, y_pred + svr.epsilon, 'k--', lw=1)
plt.plot(X_plot, y_pred - svr.epsilon, 'k--', lw=1)
plt.legend()
plt.show()