熔盐堆主回路压力损失优化

熔盐堆主回路最小压力损失设计

第四代熔盐反应堆

这些反应堆的发展规划已制定，以便至少有一部分能够在2020至2030年投入使用，届时目前使用的反应堆将寿命到期。这些反应堆能够安全且经济地为我们提供充足的能源。熔盐将用作冷却剂；这类物质可使反应堆在更高温度下运行，从而提高效率。

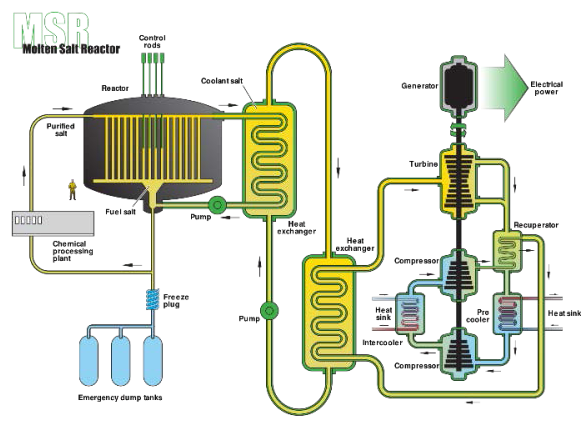
从核能长期使用的角度来看，必须确保反应堆有足够的燃料供应。因此有必要引入快中子反应堆，它们可以使用钚Pu以及铀238U作为燃料。在快中子增殖反应堆构型下，能够提供足够持续数千年的燃料[1,2]。

熔盐堆主回路

核燃料直接溶解在一回路的氟化物熔融盐中，并在石墨周围流动慢化剂以及溶解的裂变产物。这种类型的反应堆具有多个优点：它拓宽了核燃料处理的可能性（包括使用贫化钍‐铀循环的钍‐铀循环），并可在钍‐铀循环中采用快中子增殖反应堆模式；同时实现了对整个反应堆更好的“在线”控制（燃料为液态、均匀分布，因此无需像使用固体推进剂的反应堆那样进行与燃料更换相关的所谓换料周期）[5]。

反应堆参数	参考值
假设功率	1000 兆瓦电
冷却剂进出口温度	565/700 °C，压力为约 0.5 MPa
比体积功率	22 MWt/m³
净效率	44% 至 50%

另一方面，这种类型的反应堆对腐蚀和材料致密性非常敏感（连续运行、溶解有核燃料和裂变产物的熔盐对结构材料的腐蚀活性增强）。该反应堆概念可能在所有第四代反应堆类型中提供最大的综合效益（特别是在其快中子增殖堆版本中），但同时也面临最大的技术挑战，尽管已成功通过测试。这些先进反应堆应包含迄今为止已知的所有积极经验；它们代表着所需的安全标准、高运行可靠性、长期生命周期以及与其他能源相比的经济竞争力。燃料由铀的熔融氟化物组成

UF4或钚PuF3溶解在熔融氟化物LiF + BF2+ NaF的混合物中，在熔盐堆反应堆内循环。燃料将以铀、钠和锆的熔融氟化物形式存在，慢化剂为固体石墨。所用盐的熔点为425至510 °C，在约550至750 °C的工作温度下具有良好的流动性。这些盐不与空气或水发生剧烈反应，显著减少了结构设计问题。蒸汽压很低，因此系统可非承压运行。这些盐具有优良的腐蚀特性，且已有部分适用于此类系统的材料通过测试，例如钼镍铬合金（Škoda JS）[6]。

一回路用氟化物盐材料性能的测定与组成

选择盐混合物时，要求熔化温度为。最低运行温度考虑为Tmin= Ttav+ 100 °C，该值的确定基于快中子钠冷反应堆项目的经验以及PuF3溶解度的变化情况。在采用钍循环的MSBR（熔盐增殖堆）项目中，最低运行温度与熔化温度之差采用了66 °C。这可能对换热器设计产生有利影响，但降低最低运行温度也会减少三氟化物的溶解度。长期运行的最高温度为Tmax C，该值是根据哈氏合金N型材料性能 [8]确定的。

特性与考虑摩尔浓度 [g 摩尔⁻¹ ] 的方程	温度	的方程	相对误差
密度 ³ ]	800 K = 527 °C		± 0.9%
	1000 K = 727 °C
粘度	880 K = 527 °C	‐ 24.606 + 0.85068 摩尔浓度	±(4 až 6)%
	900 K = 627 °C	‐ 9.041 + 0.37085 摩尔浓度
	1000 K = 727 °C	‐ 4.949 + 0.22002 摩尔浓度
热容 cₚ[kJ kg⁻¹ K⁻¹ ]	800 – 1000 K（527 – 724 °C)	cₚ = 3.73 ‐ 0.037 M	±(10 až 20)%
热导率 [W m⁻¹ K⁻¹ ]	800 K = 527 °C	– 0.01796 摩尔浓度	± 15%（总计）
	900 K = 627 °C	– 0.01796 摩尔浓度

我们将根据前面的表格确定氟化物盐的基本性质，其中M为摩尔浓度重量。盐的纯度对其使用至关重要，若不能保持纯度，可能导致结构材料的腐蚀加剧。惰性气体的纯度同样需要保证。使用氦气时，杂质（O、N、C、CO₂,水蒸气）含量应低于0.01% mol，这从氦气冷却反应堆的运行经验中可以看出[8]。

氟化物盐的优缺点

可以使用大量特定元素在不同浓度下的盐混合物来冷却反应堆堆芯。由于单组分盐的熔点高于双组分和多组分盐，因此不使用单组分盐。与大多数常用冷却剂相比，熔盐的优点通常可归纳为四点：
- 高比热容
- 高沸点
- 高温下饱和蒸气压低
- 低熔点

以下几点是氟化物盐的主要缺点：
- 对液态盐纯度要求高
- 需要彻底去除液态盐中的水分——当与H₂O接触时，会生成具有强腐蚀性的氢氟酸（HF）
- 液态盐的凝固温度相对较高
- 对结构材料要求高——高温、液态盐的腐蚀性
- 为辐射安全需设置内置二次回路[8]

熔盐堆主回路整体布局设计

在准备项目时，有必要对带有气体提升装置的均质熔盐堆进行一体化布局设计。我们需要根据堆芯尺寸初步设计压力容器，并参考MSBR项目的经验来选定壁厚 t = 60 mm。由于推荐采用高度为H < 10 m的压缩烟囱，因此在高度上受到限制。容器直径选择为Dn = 6 m，以便可在上部布置6台板式换热器和反射层区域。

不要忘记，气体提升效率受换热器和活性区所处高度的影响。问题在于体积补偿器。我们将采用与气体提升装置模型的类比，从而获得释放气体（氦气）的空间。我们建议设置通道，通道之间留有足够空间用于布置控制棒以及向气体提升装置供应氦气，并将一次盐输送到特定的热交换器。二次盐向压力容器的输送需要在反应堆压力容器上安装传感器。在压力容器底部设有冻结阀

用于排空一次盐的容器设计。初步设计能够解决其他任务，例如：
- 带有冻结阀的被动冷却次临界容器的氦管理方案，可实现紧急停堆。
- 反应堆调节方案。
- 固体裂变产物过滤方案。
- 压力容器壁屏蔽的计算。

气体提升效率随着压力耗散的最小化而提高，即通过优化管道设计、90度弧形弯头、坡口加工、缩径、延伸段等实现。

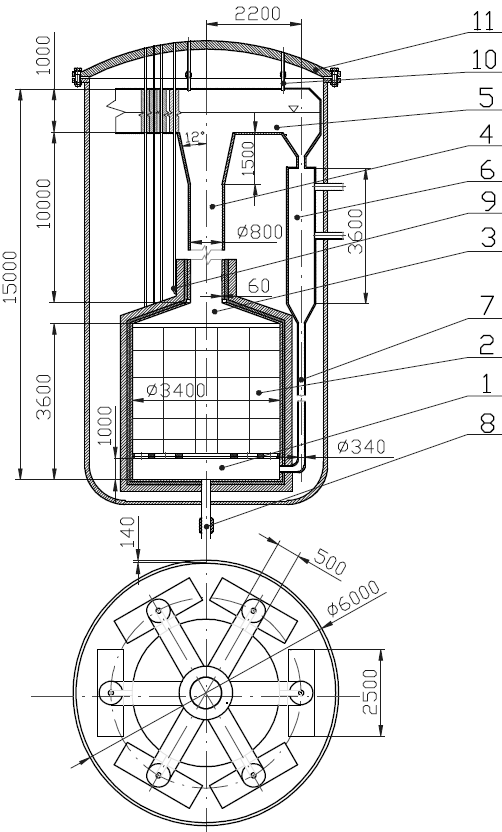
我们将在烟囱底部安装一个环形装置，将惰性气体（氦气）送入该环形装置，并通过孔洞将其注入烟囱。这样可降低氟化物盐的密度，改善循环效果。排出的气体将被回收利用，并去除其中的气态裂变产物后进行净化，随后再次用于回路中。

位置	描述	位置	描述
1	混合室	7	冷腿
2	Core	8	出口阀
3 4	过渡到烟囱 烟囱	9	环形‐氦气入口
		10	氦气出口
5	体积补偿器	11	上集流管
6			逆换流热器

在主MSR回路中使用气体提升具有诸多优点。移除需要电源运行的机械设备，显著提高了核能装置的可靠性和安全性。

所有机械设备均位于堆芯外部，因此可在反应堆运行期间通过切换至备用设备进行维修和调整。此外，另一优势是能耗较低，并且该技术可用于工作温度高于1000°C的反应堆，而目前尚无适用于该温度条件的泵。当前工业泵的工作温度上限为600°C，而新一代可耐受高达700°C的泵正逐步投入使用[4]。

熔盐堆主回路压力损失计算

核反应堆的热工水力计算，以及所有部件和一回路本身的物理、强度和技术经济计算，旨在优化一回路设计并确保核安全性。

热工水力计算与物理计算共同确定了沿堆芯横截面和高度方向由核反应释放的热功率。进一步的计算确定了通过堆芯的载热剂流量、混合表面及内部的温度、循环回路中的压力以及流经一回路介质的其他参数。因此，有必要了解或估算一回路及其工况参数的热工水力特性，以及各反应堆部件的结构材料和热工水力特性。[3]

一回路的设计计算按如下步骤进行：

一回路水力损失的计算过程

首先，我们将定义一回路的基本尺寸（图2）。

我们将考虑均质熔盐堆反应堆反应堆容器中的一体化结构。高温反应堆一回路的主要结构材料是石墨及其复合材料。

在继续之前，有必要列出局部损失清单，并考虑通过结构修改来减小这些损失。一回路各部件的尺寸、高度数据、温度以及堆芯外的次临界检查等参数均应逐一列出。

我们需要根据要求确定堆芯的主要参数——例如，可以通过效率根据电力生产的要求来确定热功率。

$$
\Phi_{th} = \frac{\Phi_{el}}{\eta}
$$

为了确定热功率，我们将选择平均比功率q，用于气举：

$$
q = 25 \div 40\ \text{MWt/m}^3
$$

根据上述数据，可以确定堆芯体积V，以及合适的直径D和高度H。烟囱的直径d可根据次临界条件（kef < 1）确定。

我们将根据一回路设计，从自由流动出发计算理论质量流量 $ \dot{m}_0 $。

$$
\dot{m}_0 = A \cdot \rho \cdot v
$$

我们已知如何根据上述公式确定质量流量。我们将选择一种方法来计算气体提升。对于核反应堆而言，最合适的模型是分散泡流模型，因为它能够最大程度地强化自然循环，并确保无冲击运行。

我们可以通过以下关系确定各个部分的流速：

$$
v_i = \frac{\dot{m}_i}{\rho_i \cdot A_i}
$$

为了计算总损失，必须考虑每个部分的摩擦损失

$$
\Delta p_{fric,i} = \lambda_i \cdot \frac{L_i}{D_i} \cdot \frac{\rho_i \cdot v_i^2}{2}
$$

和局部损失

$$
\Delta p_{loc,i} = \zeta_i \cdot \frac{\rho_i \cdot v_i^2}{2}
$$

p部件中的总摩擦损失将为：

$$
\Delta p_{total,i} = \Delta p_{fric,i} + \sum \Delta p_{loc,i}
$$

在确定总压降后，我们能够通过使用气举[3,4,7]来确定一回路中自然循环的实际稳定质量流量 $ \dot{m}_{real} $。

$$
\dot{m} {real} = \sqrt[3]{2 \cdot A \cdot g \cdot \beta \cdot \Delta T \cdot H \cdot \rho \cdot c_p \cdot \Delta p {total}^{-1}}
$$

where:
$ \dot{m} {real} $ — real mass flow rate in a balanced state
$ \rho $ — mean density of a coolant in a circuit
$ g $ — gravity acceleration
$ \beta $ — thermal expansion coefficient
$ H $ — mean heights of locations of a heat exchanger and core in a primary circuit
$ c_p $ — thermal capacity of the coolant
$ \Delta p {total} $ — total hydraulic losses in a primary circuit

关系式(8)显示了携带流区域对质量流量的立方依赖关系。当使用“气举”时，对于具有横截面的烟囱，以下成立

$$
A_s = \frac{\pi}{4} \cdot d_s^2
$$

根据质量守恒定律

$$
\dot{m} {mix} = \dot{m} {real} + \dot{m}_{gas}
$$

对于使用 $ \dot{m} {mix} $，通常需要针对双相混合物使用 $ c_p $ 和 $ \rho $，同时确定新增损失，因为 $ \dot{m} {mix} $ 会增大一回路中的流速。通过m个孔洞向气体提升烟囱中注入的气体体积，在 $ p_{in}, p_{out} $ 条件下可由以下表达式确定：

$$
V_{gas} = C_d \cdot \frac{\pi}{4} \cdot d_h^2 \cdot \sqrt{\frac{2 \cdot (p_{in} - p_{out})}{\rho_{gas}}}
$$

其中：
$ C_d $ — 耗散系数
$ d_h $ — 孔洞直径
$ p_{in} $ — 节流孔前气体压力
$ p_{out} $ — 节流孔后气体压力

根据盎格鲁‐撒克逊文献，耗散系数由以下关系确定：

$$
C_d = 0.6 + 0.4 \cdot e^{-Re/10000}
$$

以下关系适用于临界系数

$$
\zeta_{crit} = \left( \frac{p_{out}}{p_{in}} \right)^{2/(k+1)} = \left( \frac{2}{k+1} \right)^{k/(k-1)}
$$

评估与结论

计算的目的是优化基本回路尺寸，并总结具体的局部和摩擦损失，见图2，其中列出了各个局部和摩擦损失，这些损失是针对反应堆整个一回路进行计算的，结果见表3。一回路各部分的耗散系数“ζ”也已计算。需要指出的是，在串联主回路中计算压力损失时，损失是累加的；而在并联系统中，损失仅计算一次。这意味着在具有六个回路的情况下，由于是并联系统，六个或更多回路的压力损失将相同。

下表总结了各部件中的压力损失。显然，最大的局部压力损失发生在混合室入口处，该损失可通过入口颈渐扩来减小；这是一个需要在未来予以更多关注并进行更详细和精确解决的细节问题。

Component	部件名称	压力损失
1.	Core	3.3 Pa
2.	烟囱入口（锥形限制）	27.7 Pa
3.	烟囱	14550.7 Pa
4.	烟囱出口（锥形扩张）	721.6 Pa
5.	通道	360.7 Pa
6.	热交换器入口 (锥形收缩)	512.2 Pa
7.	热交换器	22800 Pa
8.	换热器出口 (锥形扩张)	256.5 Pa
9.	冷腿	24943.3 Pa
10.	冷腿弧段	10477.1 Pa
11.	混合室入口	62451.7 Pa
12.	混合室筛网	55000 Pa
13.	总压降 一回路	0.196 MPa

该计算旨在提供更具体的局部和摩擦耗散示例，以及定义这些耗散的关系，并验证哪些参数或尺寸对给定的耗散影响最大。由于我的水力计算必须与物理和热力计算相一致，因此我充分考虑了各个参数和尺寸的微小变化。主要目标是设计一个回路，用于后续项目，以对该问题提供更详细的解决方案。