pytoch学习笔记第一期

原创已于 2025-03-12 12:49:18 修改 · 1.5k 阅读

40 ·

CC 4.0 BY-SA版权

文章标签：

#学习 #笔记 #python

于 2025-03-11 18:37:05 首次发布

1.数据操作

广播机制

a=torch.arange(3).reshape((3,1))
b=torch.arange(2).reshape((1,2))
a,b

output:

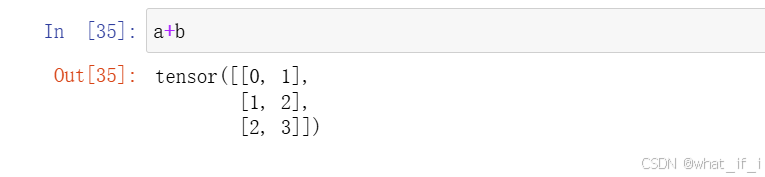
如果两张量的维度相同，那么即使行列不相等也能进行加减操作，即numpy中的广播机制

这时候会把两个张量扩增到相同的行列，再进行相加，比如这里都是3行2列。

特别注意，这种机制使用条件苛刻，不是所有情况都能用！！

不能广播，有特定要求：如果两个数组在某个维度上的大小不同且都不为1，则会引发错误。

数据读取

X[-1] 读取最后一行

X[1:3] 读取第二行和第三行

数据赋值

X[a,b] = y 单个赋值

X[a:b,:]=y 区域赋值，即第a+1行到第b行的所有元素都赋值为y

原地操作

x=x+y 进行该操作后，x会分配一个新的地址空间，与原空间不同

而x+=y 和 x[:]=x+y 都会原地操作，即地址空间不改变

2.数据预处理

创建csv文件

.csv 文件

是逗号分隔值文件（Comma-Separated Values）的通用扩展名，是一种纯文本格式的数据存储文件。

结构：

每一行代表一条数据记录（类似数据库中的一行）。
列之间通过 逗号（,） 分隔（也可以用其他符号如分号 ; 或制表符 \t，但最常见的是逗号）。
第一行通常是 列标题（可选）。

用pandas读取文件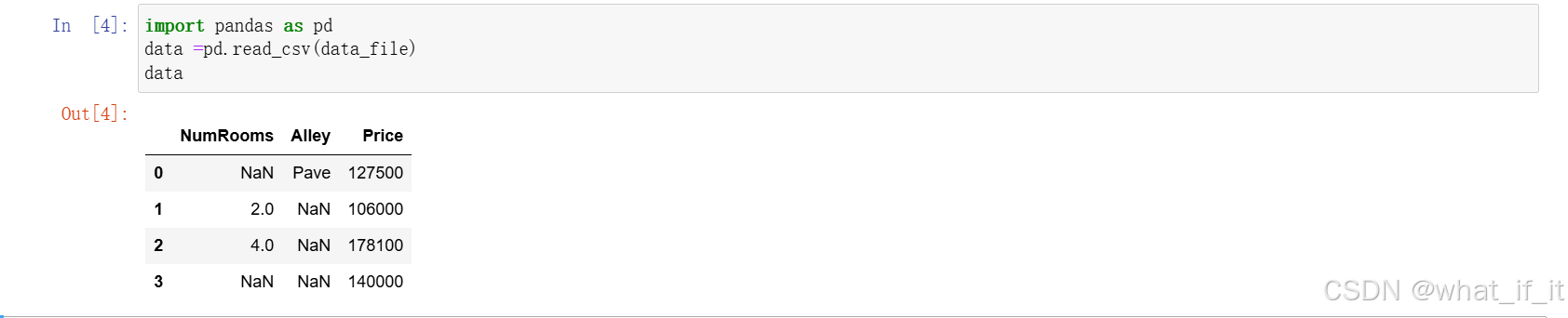

Pandas中的两种数据结构

DataFrame：二维表格型数据结构，类似 Excel 表格或 SQL 表。
# 示例：创建一个 DataFrame
data = {
    '姓名': ['Alice', 'Bob', 'Charlie'],
    '年龄': [25, 30, 35],
    '分数': [90, 85, 95]
}
df = pd.DataFrame(data)
Series：一维数组型数据结构，类似 Excel 列。
s = pd.Series([1, 2, 3], name='数值')

数据预处理

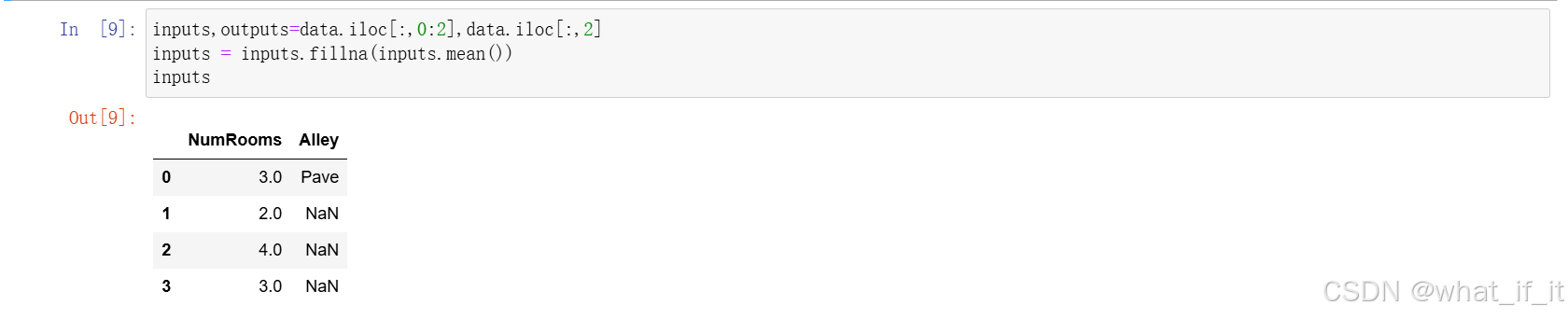
分别读入第1列，第2列数据到Inputs，第3列数据读入outputs，为接下来的数据预处理做准备；

代码中的第二行，inputs.fillna(input.mean())的作用是为inputs数据每列的Nan值数据用该列平均值填充，这里由于第二列数据是字符串类型，所以无法填充，我们用下面另一个方法解决。

用get_dummies(inputs,dummy_na=True)函数处理第二列Nun值数据，即为Nun值数据单独划分出一列来，Pave值也划分一列（即把nan看作一类，与其他不同类值一起划分出来）。

pd.get_dummies() 是 Pandas 中用于 独热编码（One-Hot Encoding） 的核心函数，将分类变量（Categorical Variables）转换为数值型矩阵，每一列代表一个分类值，通过二进制（0/1）表示是否属于该类别。

其他处理方法如下：

# 处理缺失值
df.dropna() # 删除缺失行
df.fillna(0) # 用0填充缺失值

# 过滤数据
df[df['年龄'] > 30] # 筛选年龄大于30的行

转换为tensor数据类型

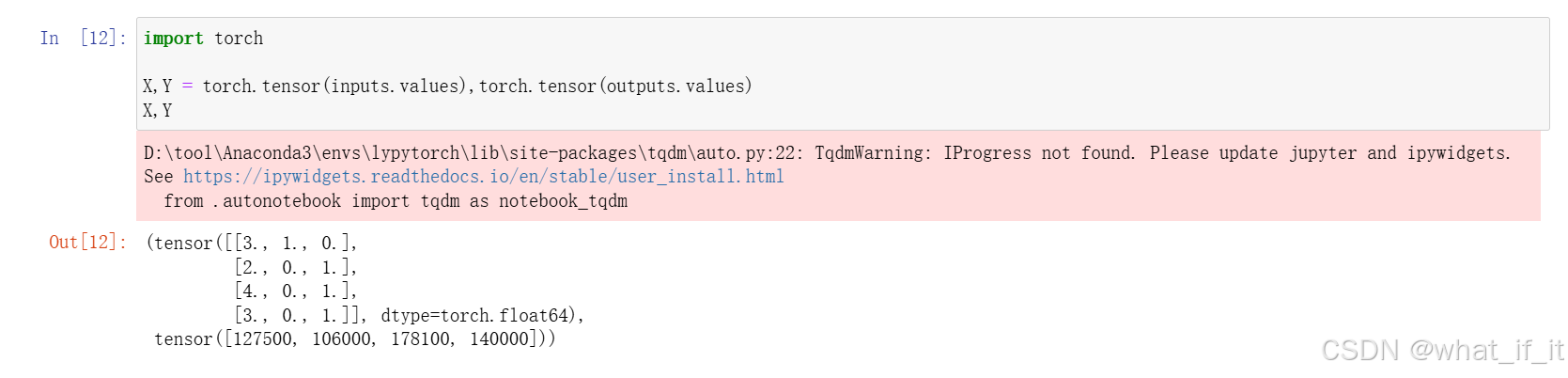
克隆

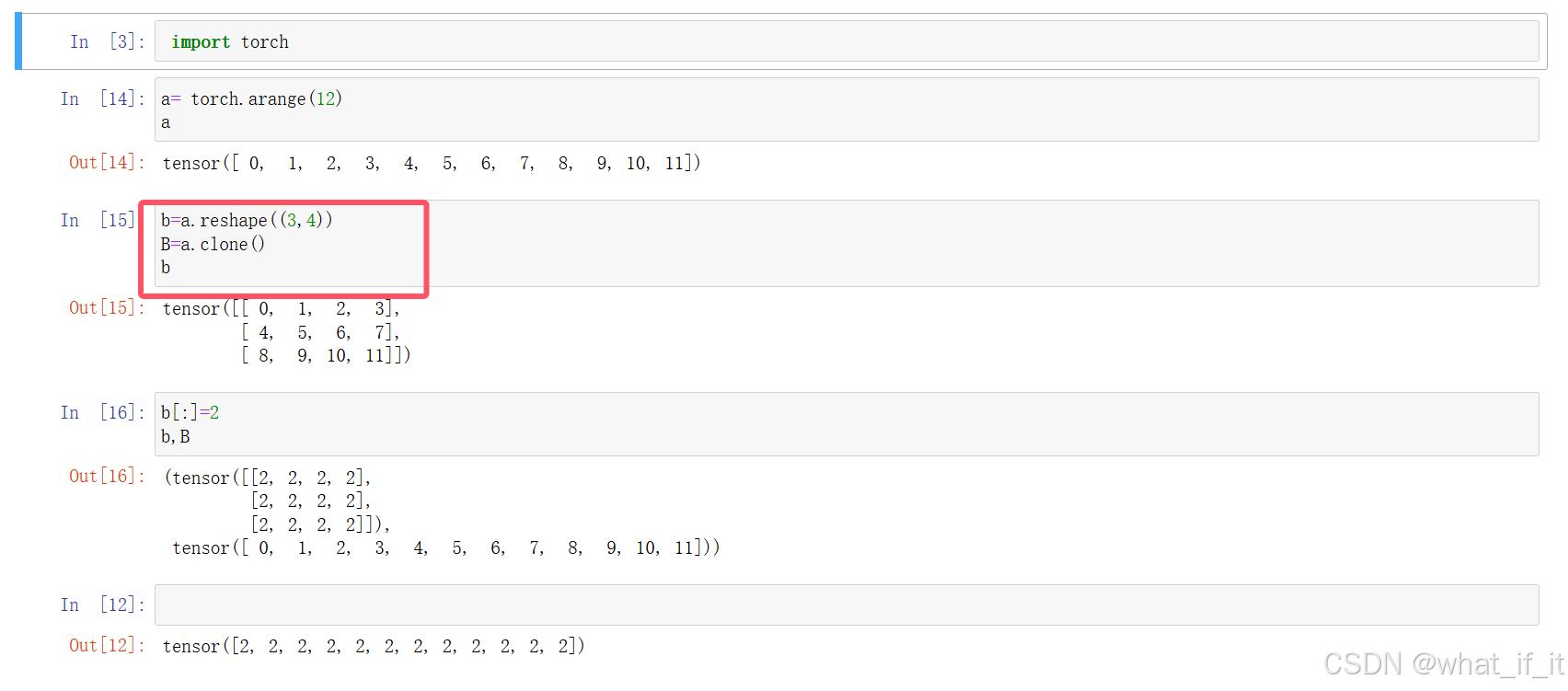
可以看到，若我们直接指代b=a，相当于是C++中的指针，b直接引用的是a原来的地址，即此时改动b，a的数据会发生变化；

而操作B=a.clone()，是创立了一个副本空间，占额外内存。

3.矩阵操作

两个矩阵按元素相乘称为哈达玛积

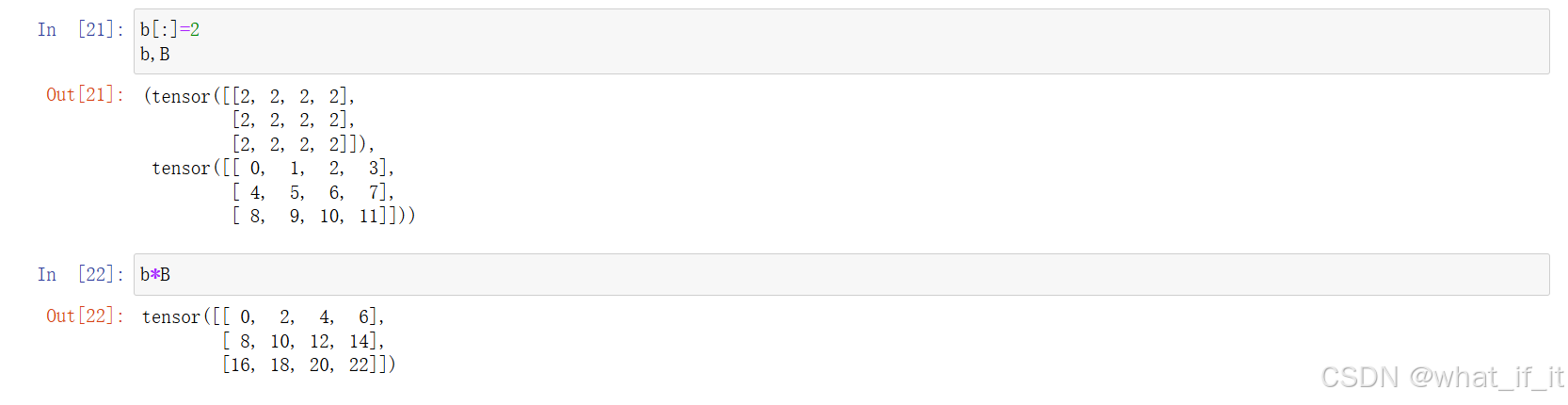
A*B，即A，B同行同列的元素做乘法得到的值填入新矩阵的该行该列。

按维度计算

加上参数（axis=i）即对矩阵按照第i个维度进行相应计算。

注意：此时维度有改变

若不想维度有改变，可以加上keepdims=True的参数

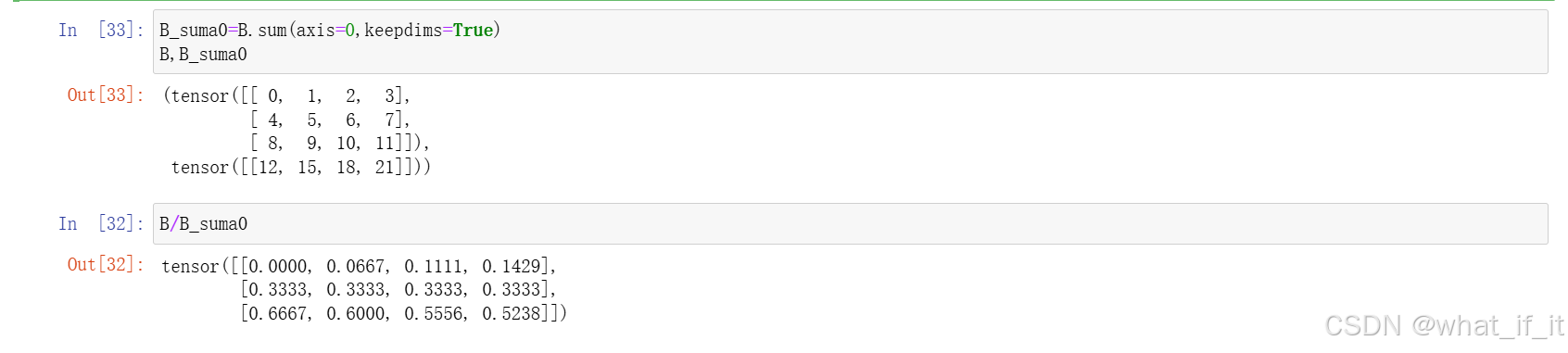
可以看到，虽然显示是降维后的结果，但实际上矩阵维度保持不变，比如这里第一维度的值都用1填充。

进而可以在不改变矩阵维度的情况下使用广播机制。

向量点乘

torch.dot(x,y),对向量x和向量y点乘:求积求和。（向量内积，是一个数，标量）

和torch.sum(x*y)等价

4.计算梯度

存储梯度

x.requires_grad_(True)存储梯度

x.grad 访问梯度

反向传播函数

调用反向传播函数来自动计算y关于x每个分量的梯度

重置梯度

注意：由于torch默认情况下，会累计梯度，所以需要清除之前的值

即 .grad.zero_()，赋于0值

设置常量

u = y.detach(),把u设置为值得大小为y即x*x的常数值，此时求梯度时，u看作常数，不再链式求导。

注意：y.sum().backward()

这里为什么要先sum（）求和，再求梯度？

因为，若不求和，那么y的反向传播所求梯度值会显示为一个梯度矩阵，而pytorch里一般无法处理这种情况；实际上往往应该对其所有属性求导后再加和，得到了这个样本的偏导数之和。

参考：【深度学习】自动求导中有时为什么要先sum()再backward()_sum().backward()-优快云博客