详解#Z0698. 差分入门-优快云博客

本文链接：https://blog.youkuaiyun.com/weq2011/article/details/129149142

文章介绍了使用线段树和差分两种方法来解决区间更新查询的问题，提供了详细的代码实现，并建议读者先学习相关的基础知识。线段树适用于复杂操作，而差分法则更简洁。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

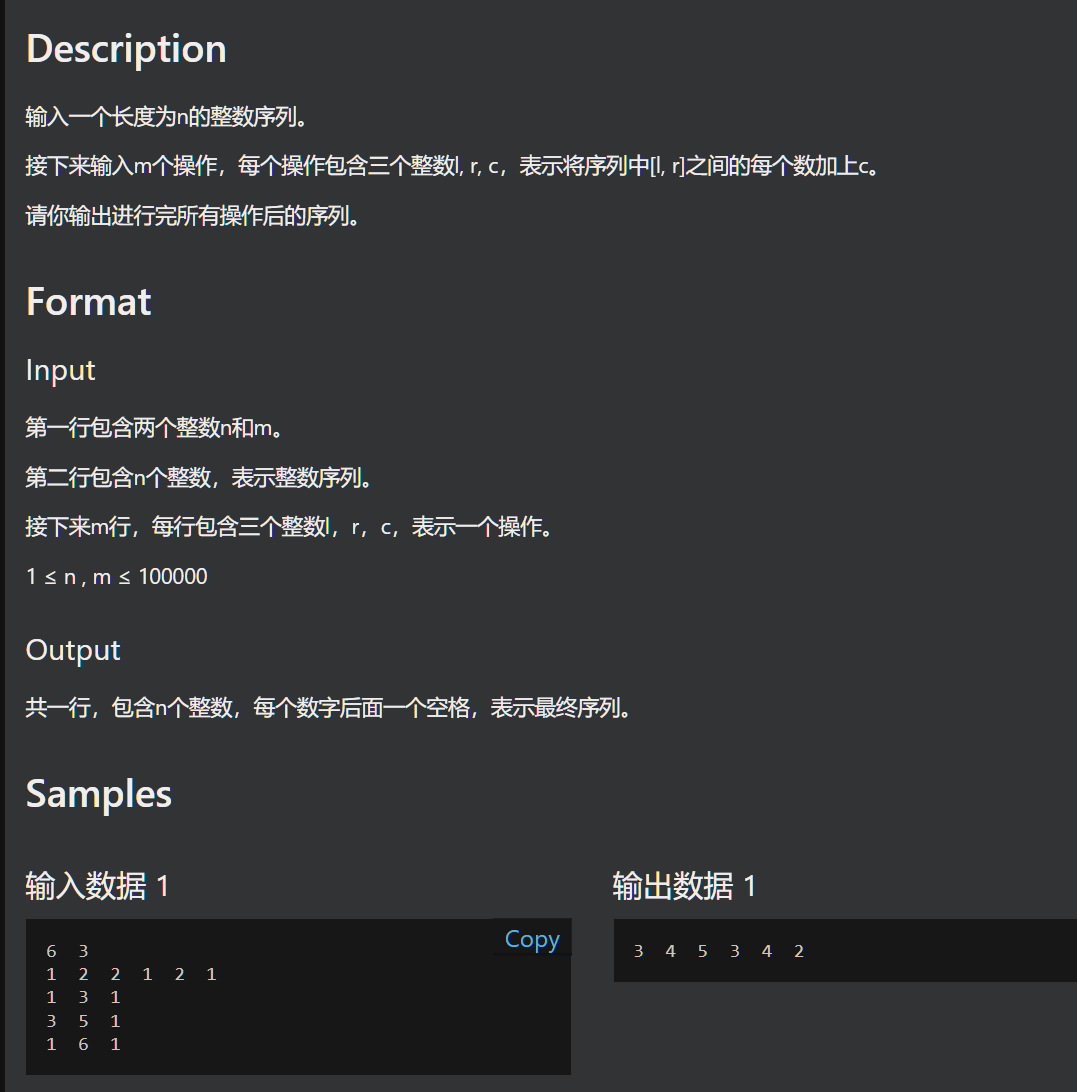
做法.1线段树

我才不会告诉你我第一次做的时候是用线段树AC的

建议先康康超详解线段树(浅显易懂,几乎涵盖所有线段树类型讲解,匠心之作,图文并茂)

代码.1线段树

#include <bits/stdc++.h>
#define int long long
using namespace std;
int sumv[10000001],n,m,a[10000001],lazy[10000001];
void bui(int id,int l,int r)//创建线段树,id表示存储下标,区间[L,r]
{
  if(l == r)
  {
    //叶子
    sumv[id] = a[l];
    return ;
  }
  int mid = (l + r) / 2;
  bui(id * 2,l,mid);
  bui(id * 2 + 1,mid + 1,r);
  sumv[id] = sumv[id * 2] + sumv[id * 2 + 1];
}
void pushup(int id)
{
  sumv[id] = sumv[id * 2] + sumv[id * 2 + 1];
}
void pushdown(int id,int l,int r)
{
  if(lazy[id])
  {
    int mid = (l + r) / 2;
    lazy[id * 2] += lazy[id];
    lazy[id * 2 + 1] += lazy[id];

    sumv[id * 2] += lazy[id] * (mid - l + 1);

    sumv[id * 2 + 1] += lazy[id] * (r - mid);

    lazy[id] = 0;
  }
}
void qjgx(int id,int l,int r,int x,int y,int v)
{
  if(x <= l && r <= y)
  {
    lazy[id] += v;
    sumv[id] += (r - l + 1) * v;
    return ;
  }
  int mid = (l + r) / 2;
  pushdown(id,l,r);
  if(x <= mid) qjgx(id * 2,l,mid,x,y,v);
  if(y > mid) qjgx(id * 2 + 1,mid + 1,r,x,y,v);
  pushup(id);
}
int find(int id,int l,int r,int x,int y)
{
  if(x <= l && r <= y) return sumv[id];
  pushdown(id,l,r);
  int mid = (l + r) / 2;
  int ans = 0;
  if(x <= mid) ans += find(id * 2,l,mid,x,y);
  if(y > mid) ans += find(id * 2 + 1,mid + 1,r,x,y);
  return ans;
}
signed main()
{
  cin>>n>>m;
  for(int i = 1; i <= n; i++) cin>>a[i];
  bui(1,1,n);
  while(m--)
  {
    int k,x,y,p;
    cin>>x>>y>>k;
    qjgx(1,1,n,x,y,k);
  }
  for(int i = 1; i <= n; i++) cout<<find(1,1,n,i,i)<<' ';
  return 0;
}

做法.2差分(正解)

建议先看看一维,二维差分の详解 ,里面讲解了这道题。(★ ω ★)

代码.2差分

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,m,a[1000001],s,c[10000001];
void bil()
{
  for(int i = 1;i <= n;i++) c[i] = a[i] - a[i - 1];
}
void gexi(int x,int y,int z)
{
  c[x] += z;
  c[y + 1] -= z;
}
signed main()
{
  cin>>n>>m;
  for(int i = 1;i <= n;i++) cin>>a[i];
  bil();
  while(m--)
  {
    int x,y,z;
    cin>>x>>y>>z;
    gexi(x,y,z);
  }
  s = c[1];
  cout<<s<<' ';
  for(int i = 2;i <= n;i++) s += c[i],cout<<s<<' ';
  return 0;
}