#B. gsy 的装备配置

最新推荐文章于 2025-07-31 12:29:15 发布

Ia_aIweq

最新推荐文章于 2025-07-31 12:29:15 发布

阅读量151

点赞数 1

CC 4.0 BY-SA版权

分类专栏：数学文章标签： c++

本文链接：https://blog.youkuaiyun.com/weq2011/article/details/128901703

数学专栏收录该内容

44 篇文章

订阅专栏

文章介绍了一种利用正难则反的思考方式，将原本O(n^2)复杂度的算法优化到O(n)。通过计算前缀和，对数字进行分段处理，可以有效地解决题目中关于数字转换的问题。提供的C++代码展示了如何实现这一优化策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

思路

可以采用正难则反的思想。

如果我们希望x是答案，那么只要让所有数字减到离x最近的倍数(同时该倍数也必须<=x)的就可以了

这样的话是 O(n^2)的复杂度

但是数据很大，所以只能 O(n)或者O(log(n))来做

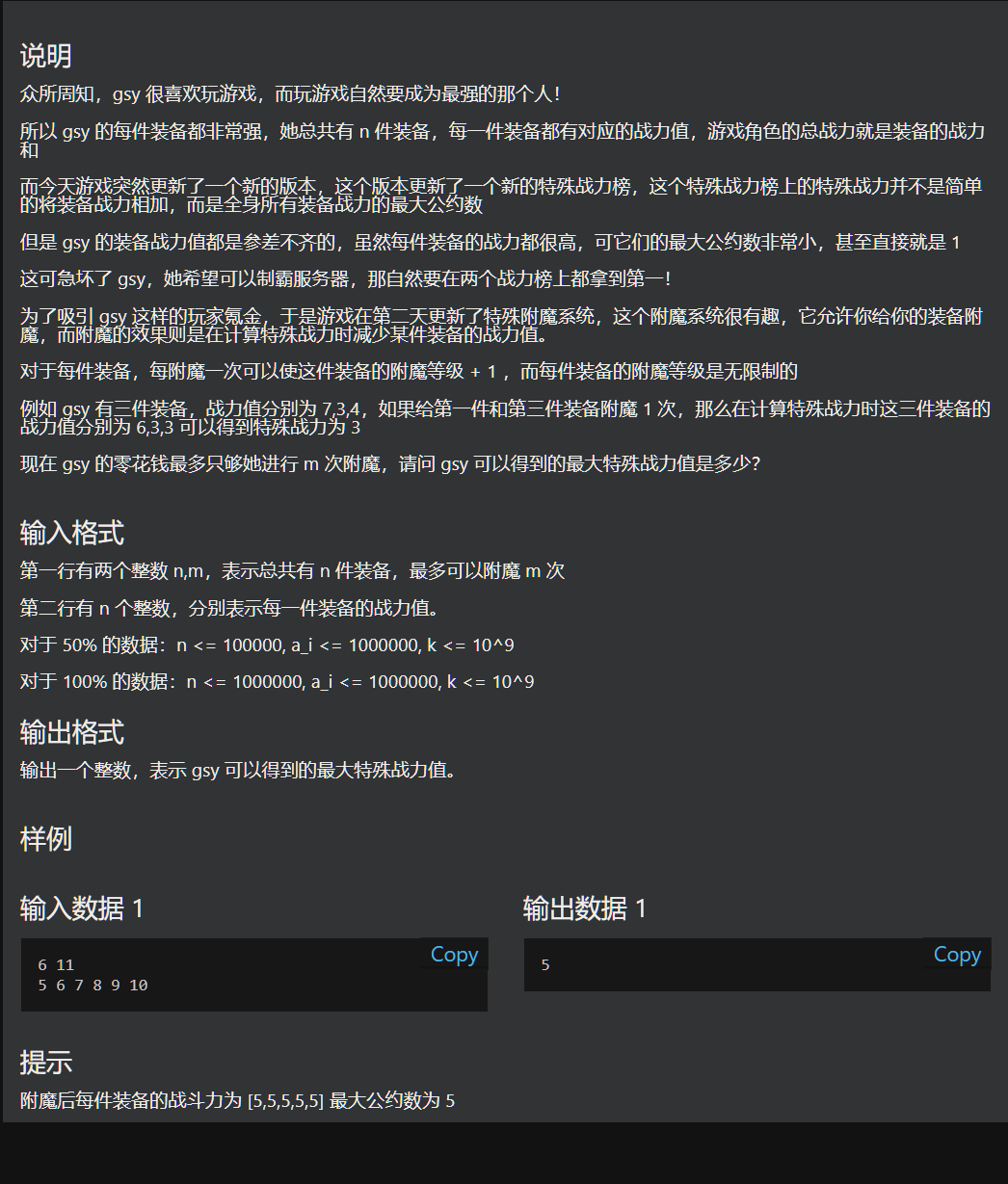
那么我们可以设 pre[i]是下标小于i的数字数量,

sum[i]是下标小于i的数字总和

其实对于x来说，对于某一段区间[k*x,(k+1)*x-1]里的所有数字，都是变化成k*x的

那么我们可以用前缀和计算出该区间的数字和-k*x*该区间的数字个数就可以计算出结果，

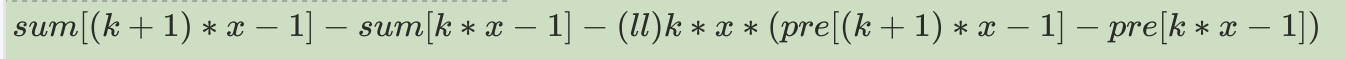
代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
int ans,n,m,pre[10000001],cnt[10000001],t,sum[10000001];
bool f(int x)
{
  int s = 0;
  for(int k = 0; k * x <= 1000001; k++)
    s += (sum[x * (k + 1) - 1] - sum[k * x - 1] - (int)k * x * (pre[x * (k + 1) - 1] - pre[k * x - 1]));
  if(s <= m) return 1;
  return 0;
}
signed main()
{
  scanf("%lld%lld",&n,&m);
  for(int i = 1; i <= n; i++)
  {
    scanf("%lld",&t);
    cnt[t]++;
  }
  for(int i = 1; i <= 2000000; i++) sum[i] = sum[i - 1] + cnt[i] * i;
  for(int i = 1; i <= 2000000; i++) pre[i] = pre[i - 1] + cnt[i];
  for(int x = 1; x <= 1000000; x++)
    if(f(x))
      ans = x;
  printf("%lld",ans);
  return 0;
}
/*
5 2
5 6 7 6 5
*/