算法设计与分析学习笔记

一、基础部分

1.1 复杂度

可参考学习复杂度 - OI Wiki (oi-wiki.org)

二、蛮力法

2.1 原理

蛮力法也称穷举法(枚举法)或暴力法，是一种简单的直接解决问题的方法，通常根据问题的描述和所涉及的概念定义，对问题所有可能的状态(结果)一一进行测试，直到找到解或将全部可能的状态都测试一遍为止。

2.2 排序问题

2.2.1 选择排序

可参考学习选择排序 - OI Wiki (oi-wiki.org)

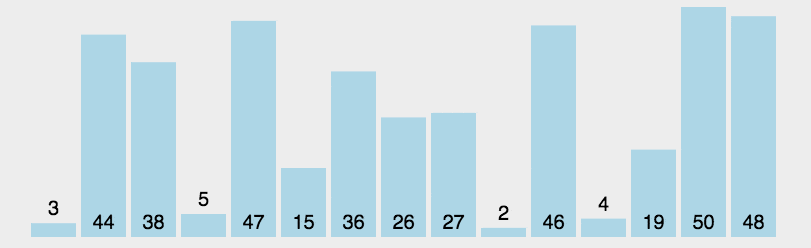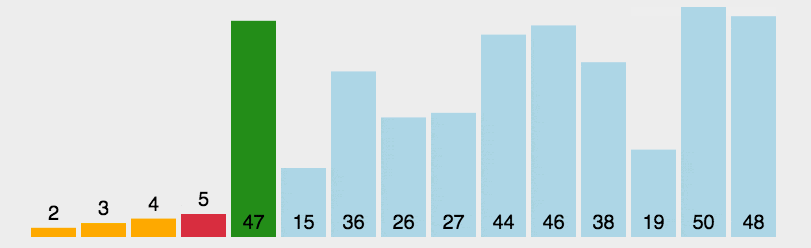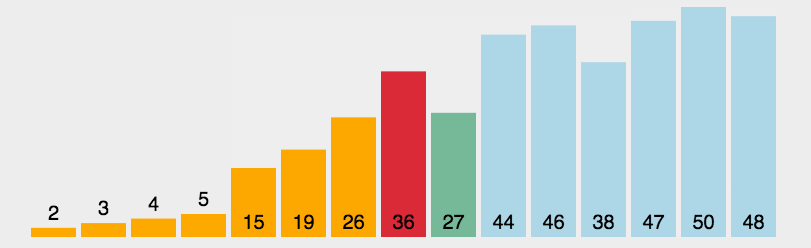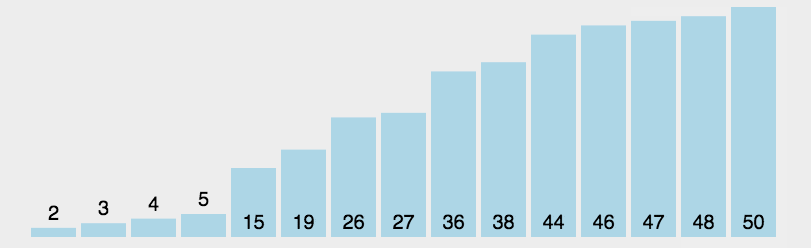
1）思想：每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。

2）时间复杂度：对任何输入来说，选择排序都是一个$O(n^2)$的算法。但键的交换次数仅为$O(n)$，这个特性使得选择排序由于许多其他的排序算法

2.2.2 冒泡排序

可参考学习1.1 冒泡排序 | 菜鸟教程 (runoob.com)

1）思想：从前到后（即从下标较小的元素开始）依次比较相邻元素的值，若发现逆序则交换位置，使值较大的元素逐渐从前移向后部。

2）时间复杂度：对于所有规模为n的数组来说，该冒泡排序的键值比较次数都是相同的，$C(n)=\frac{n(n-1)}{2}$，但它的键交换次数取决于特定的输入。在序列完全有序时，冒泡排序只需遍历一遍数组，不用执行任何交换操作，时间复杂度为$O(n)$，在最坏情况下，冒泡排序要执行$\frac{n(n-1)}{2}$次交换操作，时间复杂度为$O(n^2)$ 。

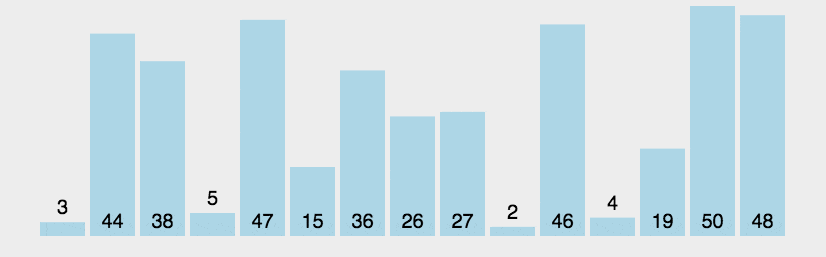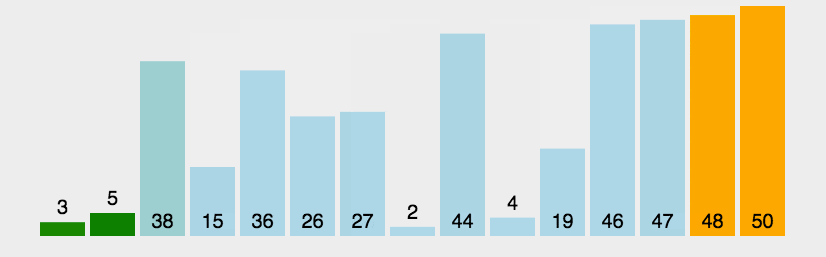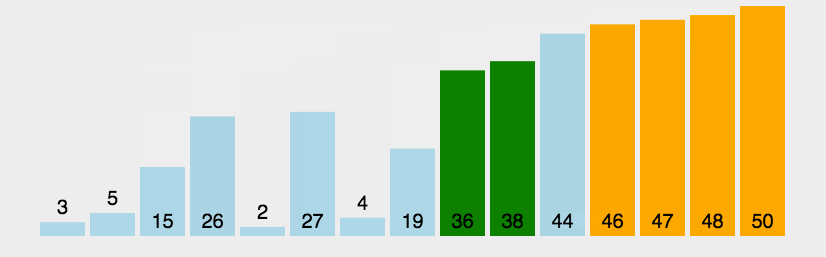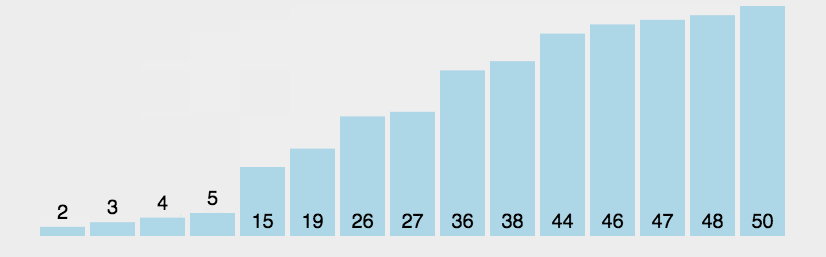
2.3 查找问题

2.3.1 顺序查找

1）思想：简单地将给定列表中的连续元素和给定的查找键进行比较，直到遇到一个匹配的元素（成功查找），或者在遇到匹配元素前遍历了整个列表（失败查找）

2）时间复杂度：顺序查找是阐释蛮力法很好的工具，无论是在最差情况还是平均情况下，该算法仍然是一个线性算法。

2.3.2 蛮力字符串匹配

1）思想：将模式对准文本的前m个字符，然后从左到右匹配每一对相应的字符，直到m对字符全部匹配（算法就可以结束了）或者遇到一对不匹配的字符。在后一种情况下，模式向右移一位，然后从模式的第一个字符开始，继续把模式和文本中的对应字符进行比较。注意，最后一轮子串匹配的起始位置是n-m（假设文本位置的下标是从0到n-1）

2）时间复杂度：最坏的情况下，时间复杂度为$O(nm)$;但事实上在查找随机文本时，时间复杂度为$O(n)$

2.4 最近对问题

1）概述：最近对问题要求在一个包含n个点的集合中，找出距离最近的两个点$d(p_i,p_j)=\sqrt{(x_i-x_j{)}^2-(y_i-y_j{)}^2}$

2）算法：分别计算每一对点之间的距离，然后找出距离最小的那一对。为了避免对同一对点计算两次距离，只考虑$i<j$的那些$d(p_i,p_j)$

3）时间复杂度：$O(n^2)$

2.5 凸包问题

可参考学习：凸包 - OI Wiki (oi-wiki.org)

1）概述：在平面或者高维空间的一个给定点集合中寻找凸包。

定义1：对于平面上的一个点集合（有限的或无限的）如果以集合中任意两点p和q为端点的线段都属于该集合，我们说这个集合时凸的。

定义2：一个点集合S的凸包是包含S的最小（S的凸包一定是所有包含S的凸集合的子集）凸集合。即是说对于平面上n个点的集合，他的凸包就是包含所有这些点（或者在内部，或者在边界上）的最小凸多边形。

2）算法：对于一个n个点集合中的两个点，当且仅当该集合中的其他点都位于穿过这两点的直线的同一边时，他们的连线是该集合凸包边界的一部分，对每一对点都做一遍检验之后，满足条件的线段构成了该凸包的边界。

检验是否位于这条直线的同一边:把每一个点代入$ax+by-c（a=y_2-y_1,b=x_1-x_2,c=x_1{y}_2-y_1{x}_2）$，其中点$（x_1，y_1）,（x_2，y_2）$为直线上的点

3）时间复杂度：$O(n^3)$

2.6 穷举查找

2.6.1 原理

生成问题域中的每一个元素，选出其中满足问题约束的元素，然后再找出一个期望元素。

2.6.1 旅行商问题

1）概述：找出一条n个给定的城市间的最短路径，使我们在回到出发的城市之前，对每个城市都只访问一次。

2）时间复杂度：$O(n!)$

2.6.2 背包问题

1）概述：给定n个重量为$w_1,w_2,\dots \dots w_n$,价值为$v_1,v_2,\dots \dots ,v_n$的物品和一个承重为W的背包，求这些物品中一个最有价值的子集，并且要能够装到背包中。

2）时间复杂度：$\Omega (2^n)$

2.6.3 分配问题

1）概述：有n个任务需要分配给n个人执行，一个任务对应一个人（每个任务只分配个一个人，每个人只分配一个任务）。对于每一对i,j=1,2,……,n来说，将第j个任务分配给第i个人的成本是C[i,j]。该问题要找出总成本最小的分配方案。

2）时间复杂度：$O(n!)$

2.7 图遍历算法

2.7.1 深度优先查找

可参考学习：01. 图的深度优先搜索知识 | 算法通关手册（LeetCode） (itcharge.cn)

1）思想：从起始节点开始，沿着一条路径尽可能深入地访问节点，直到无法继续前进时为止，然后回溯到上一个未访问的节点，继续深入搜索，直到完成整个搜索过程。

2）时间复杂度：

对于邻接矩阵表示法：$\Theta (|V{|}^2)$；

对于邻接链表表示法：$\Theta (|V|+|E|)$，其中|V|和|E|分别是图的顶点和边的数量

2.7.2 广度优先查找

可参考学习：03. 图的广度优先搜索知识 | 算法通关手册（LeetCode） (itcharge.cn)

1）思想：从起始节点开始，逐层扩展，先访问离起始节点最近的节点，后访问离起始节点稍远的节点。以此类推，直到完成整个搜索过程。

2）时间复杂度：

对于邻接矩阵表示法：$\Theta (|V{|}^2)$；

对于邻接链表表示法：$\Theta (|V|+|E|)$，其中|V|和|E|分别是图的顶点和边的数量

三、减治法

3.1 原理

同样是将一个大问题划分为若干个小的子问题，但是这些子问题不需要分别求解，只需要求解其中一个子问题便可，因此也不需要对子问题进行合并，可以说，减治法是一种退化版的分治法。

减治法可分为3种：

• 问题规模减去一个常量
• 问题规模减去常数因子
• 问题规模减去可变因子

3.2 插入排序

参考学习插入排序 - OI Wiki (oi-wiki.org)

1）思想：将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

2）时间复杂度：

对于有序数组：$\Theta (n)$

平均效率：$\Theta (n^2)$

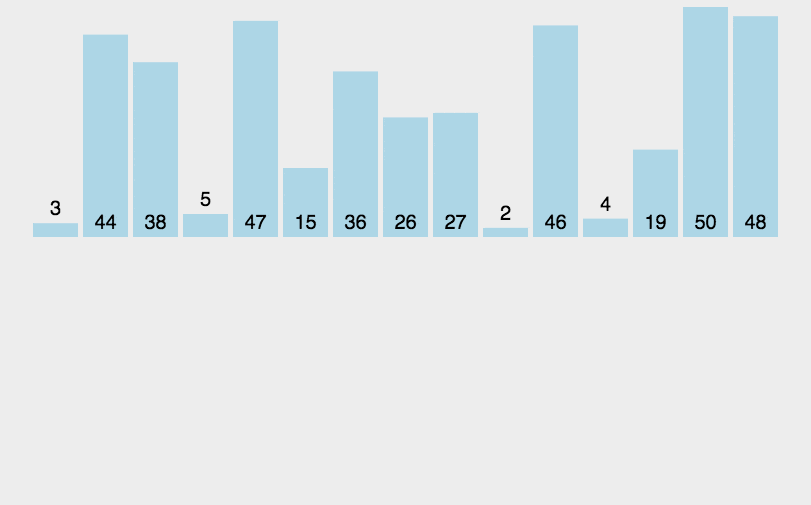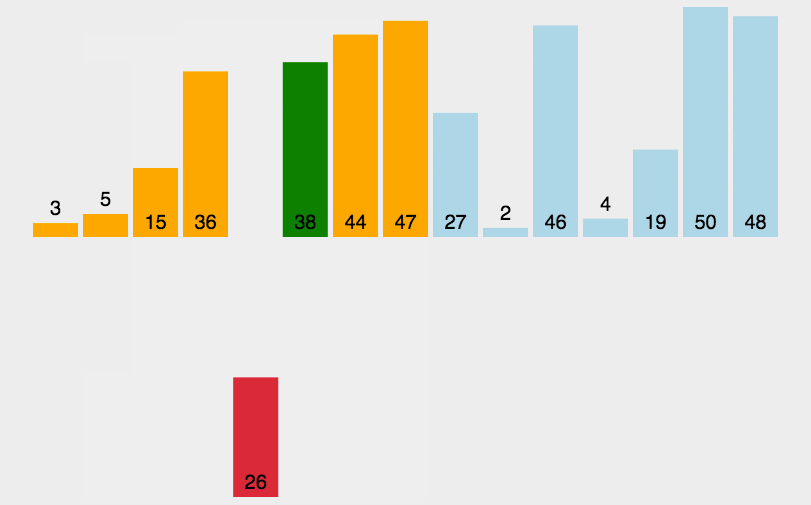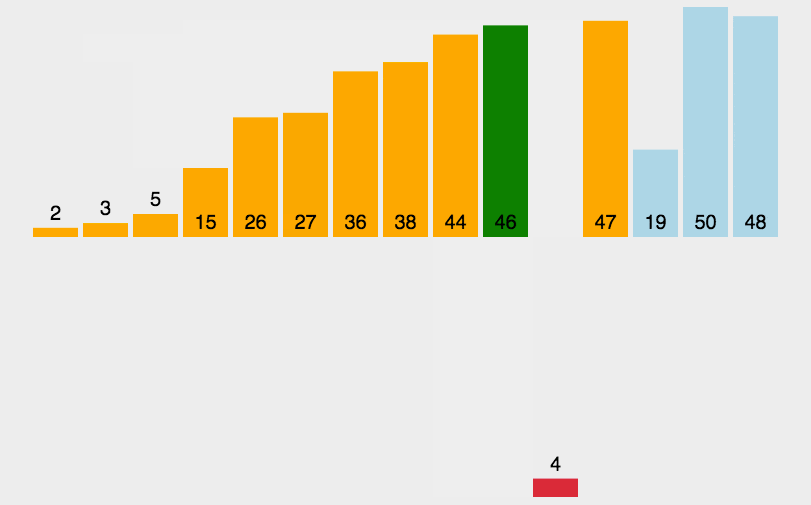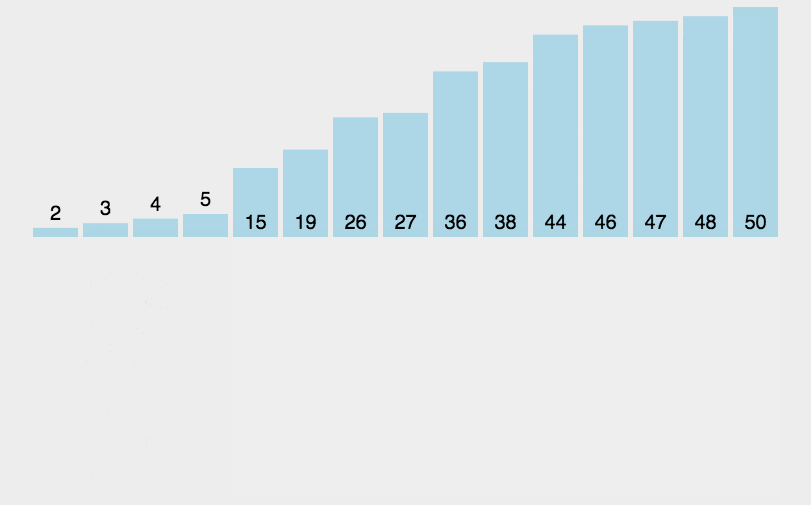
3.3 拓扑排序

可参考学习拓扑排序详解（包含算法原理图解、算法实现过程详解、算法例题变式全面讲解等）-阿里云开发者社区 (aliyun.com)

1）思想：对一个有向无环图G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

3.4 生成组合对象的算法

3.4.1 生成排列

1）概述：研究数1，2，……，n生成所有的排列问题

2）算法：

如果元素k的箭头指向一个相邻的较小元素，我们说他在这个以箭头标记的排列中是移动的

【Johnson-Trotter算法】

【字典序】

3）时间复杂度：Johnson-Trotter算法：$O(n!)$

3.4.2 生成子集

1）概述：生成抽象集合A的所有子集

3.5 减常因子算法

3.5.1 原理

减治法的第二种主要变化形式（问题规模减去常数因子）

3.5.2 折半查找

可参考学习01. 二分查找知识（一） | 算法通关手册（LeetCode） (itcharge.cn)

1）思想：通过比较查找键K和数组中间元素A[m]来完成查找工作。如果他们相等，算法结束。否则，如果K<A[m]，就对数组的前半部分执行该操作，如果K>A[m]，则对数组的后半部分执行该操作。

2）时间复杂度：

最差情况：$\Theta (logn)$

最优情况：$\Theta (1)$

3.5.3 假币问题

1）概述：在n枚外观相同的硬币中，有一枚是假币。在一架天平上，可以比较任意两组硬币，通过观察天平是右倾、左倾、停在中间来判断两组硬币的重量。设计一个高效的算法来检测这枚假币。

2）算法：把n枚硬币分成两堆，每堆有n/2枚硬币。如果n为奇数，就留下一枚额外的硬币，然后把两堆硬币放在天平上。如果两堆硬币重量相同，那么放在旁边的硬币就是假币；否则可以用同样的方法对较轻的一堆硬币进行处理，这堆硬币中一定包含那枚假币。

3）时间复杂度：$\Theta (lo{g}_{2}n)$

3.5.4 俄式乘法

1）思想：它是对两个正整数相乘的非主流算法。假设m和n是两个正整数，我们要计算它们的乘积。

它的主要原理如下：

当n为偶数时：$n\times m=\frac{n}{2}\times 2m$

当n为奇数时：$n\times m=\frac{n-1}{2}\times 2m+m$

并以$1\times m=m$作为结束条件。

3.5.5 约瑟夫斯问题

1）概述：N个人围成一圈，从第一个开始报数，第M个将被杀掉，最后剩下一个，其余人都将被杀掉。这个问题就是要求算出幸存者的号码J(n)

据说著名犹太历史学家Josephus（弗拉维奥·约瑟夫斯）有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是，给定了和，一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

2）算法：参考学习约瑟夫问题 - OI Wiki (oi-wiki.org)

3.6 减可变规模算法

3.6.1 原理

减治法的第三种主要变化形式（问题规模减去可变因子）

3.6.2 插值查找

可参考学习插值查找 - 算法与复杂度 | 小白·菜的空间 (infinityglow.github.io)

1）思想：不同于折半查找总是把查找键和给定有序数组的中间元素进行比较，插值查找为了找到用来和查找键进行比较的数组元素，考虑了查找键的值。例如在字典查找单词yell时，总是会翻到靠近结尾的地方，而不是翻到开头处。

2）时间复杂度

3.6.3 二叉查找树的查找和插入

1）概念

• 每个节点一个元素
• 所有左子树的元素都小于子树根节点的元素
• 所有右子树的元素都大于子树根节点的元素（左小右大）

2）时间复杂度：查找/插入一颗由n个随机键构造起来的二叉查找树：$\Theta (logn)$

3.6.4 拈游戏

【单堆拈游戏】

1）概述：现在只有一堆n个棋子，两个玩家轮流从堆中拿走最少1个，最多m个棋子。每次拿走的棋子数都可以不同，但能够拿走的上下限数量是不变的。如果每个玩家都做出了最佳选择，哪个玩家能够胜任拿到最后那个棋子？是先走的还是后走的

2）算法：当且仅当n不是m+1的倍数时，n个棋子的实例是一个胜局。胜利的策略是在每次拿走n mod （m+1）个棋子；如果背离这个策略，则会把胜局留给对手。

【拈游戏】

四、分治法

4.1 原理

将一个大问题划分为若干个子问题，分别求解后将子问题的解进行合并得到原问题的解。
许多分治算法的时间效率T(n)满足方程T(n)=aT(n/b)+f(n)。主定理确定了该方程解的增长次数。

4.2 归并排序

可参考学习05. 归并排序 | 算法通关手册（LeetCode） (itcharge.cn)

1）思想：先递归地将当前数组平均分成两半，然后将有序数组两两合并，最终合并成一个有序数组。

归并排序的实现有两种方法：

• 自上而下的递归；
• 自下而上的迭代；

2）步骤：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4. 重复步骤 3 直到某一指针达到序列尾；
5. 将另一序列剩下的所有元素直接复制到合并序列尾。

3）时间复杂度：$O(nlogn)$

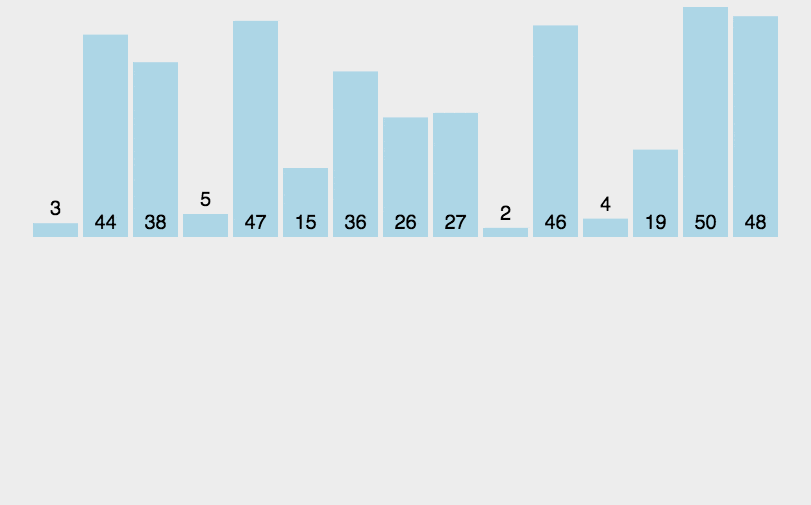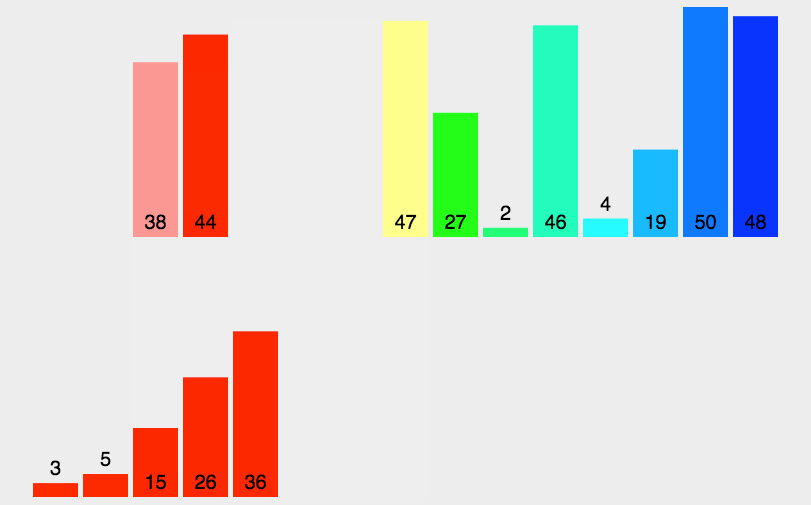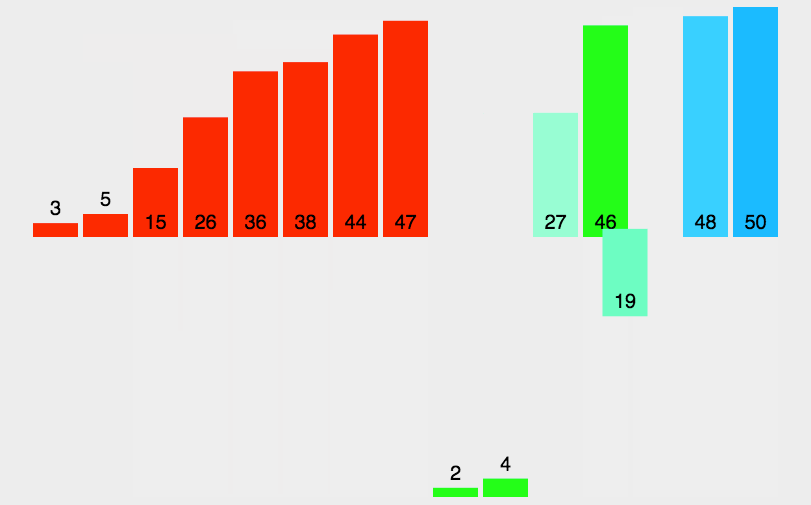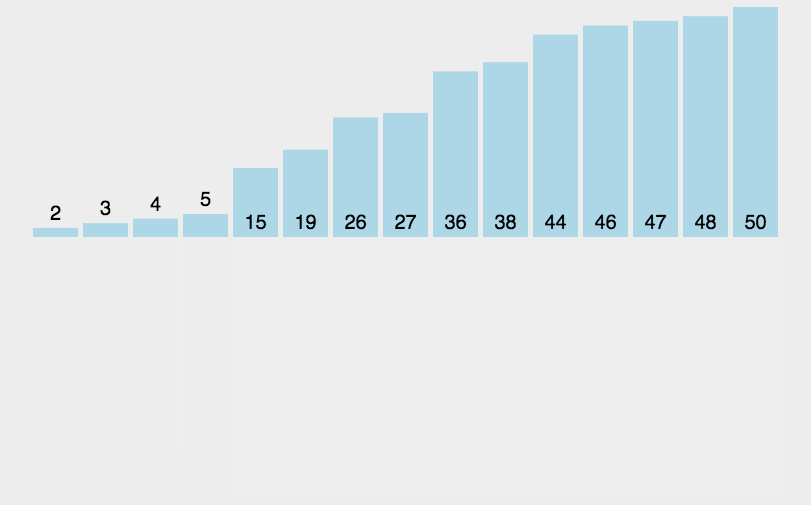
4.3 快速排序

可参考学习06. 快速排序 | 算法通关手册（LeetCode） (itcharge.cn)

1）思想：选择数组中某个元素作为基准数，通过一趟排序将数组分为独立的两个子数组，一个子数组中所有元素值都比基准数小，另一个子数组中所有元素值都比基准数大。然后再按照同样的方式递归的对两个子数组分别进行快速排序，以达到整个数组有序。

2）时间复杂度：

最优情况：$O(nlogn)$

最差情况：$O(n^2)$

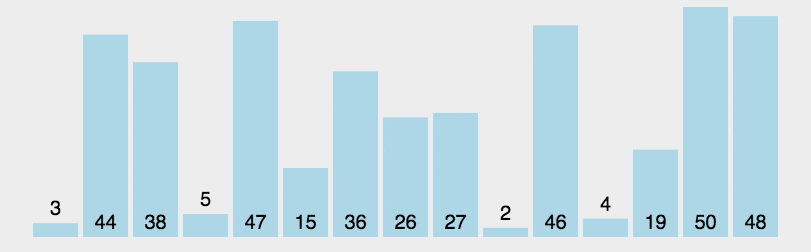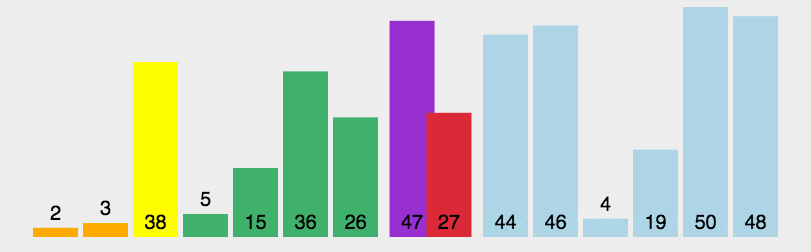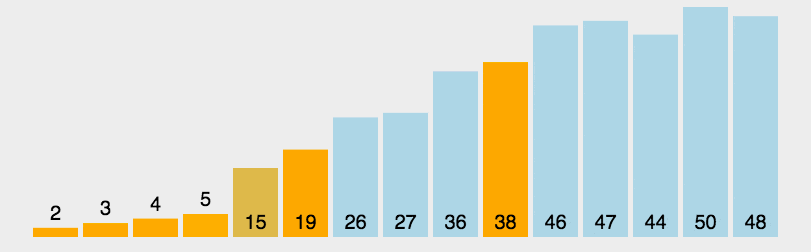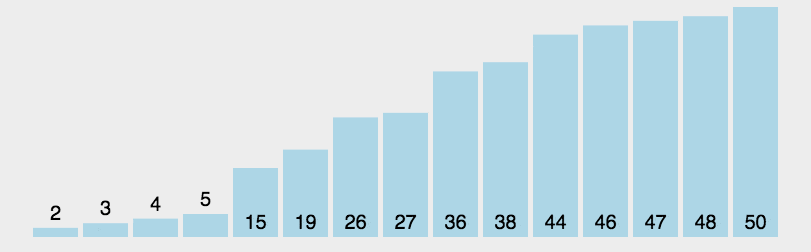
4.4 二叉树遍历及其相关特性

1）定义：我们把二叉树定义为若干节点的一个有限集合，他要么为空，要么由一个根和两颗称为$T_L$和$T_R$的不相交二叉树构成，这两颗二叉树分别为根的左右子树。我们常常认为二叉树是有序树的一种特例，见下图。

2）三种遍历算法：

• 前序遍历：根—>左子树—>右子树
• 中序遍历：左子树—>根—>右子树
• 后序遍历：左子树—>右子树—>根

3）伪代码：

算法  Height(T)
	//递归计算二叉树的高度
	//输入：一棵二叉树T
	//输出：T的高度
	if T=0 return -1
	else return max{Height(T_left),Height(T_right)}+1

4）完全二叉树：一种每个节点仅具有0个或2个子女的二叉树。

4.5 大整数乘法

参考学习【算法】大数乘法问题及其高效算法 - 夏尔_717 - 博客园 (cnblogs.com)

1）概述：对超过100位的乘法十进制整数进行乘法运算时，由于这样的整数过于长，现代计算机的一个字是装不下的，因此就需要对他们做特别的处理。

2）算法：

对于任何两位数$a=a_1{a}_0$和$b=b_1{b}_0$来说，他们的的积c可以用下列公式来计算：$c=a\times b=c_{2}10^2+c_{1}10^1+c_0$，其中$c_2=a_1\times b_1$是他们第一个数字的积；$c_0=a_0\times b_0$，是他们第二个数字的积；$c_1=（a_1+a_0)\times (b_1+b_0)-(c_2+c_0)$；

对于n位整数，其中n是偶数而言，则有$c=a\times b=(a_{1}10^{n/2}+a_0)\times (b_{1}10^{n/2}+b_0)=(a_1\times b_1)10^n+(a_1\times b_0+a_0\times b_1)10^{n/2}+(a_0\times b_0)=c_{2}10^n+c_{1}10^{n/2}+c_0$，其中$c_2=a_1\times b_1$是他们前半部分的积；$c_0=a_0\times b_0$，是他们后半部分的积；$c_1=（a_1+a_0)\times (b_1+b_0)-(c_2+c_0)$；

2）时间复杂度：$\Theta (n^{lo{g}_{2}3})$

4.6 Strassen矩阵乘法

参考学习4-2.矩阵乘法的Strassen算法详解 - 程序员修练之路 - 博客园 (cnblogs.com)

1）概述：分治法既然可以减少两个数乘法中的位乘次数，同样也可以在矩阵乘法中发挥同样作用

2）算法:

计算两个$2\times 2$矩阵A和B的积C只需要进行7次乘法运算。下图所示：

对A和B两个n$\times$n矩阵的计算也同理（如果n不是2的乘方，矩阵可以用为0的行或列来填充），可以把A,B,C分别划分为4个(n/2)$\times$ (n/2)的子矩阵

3）时间复杂度：$\Theta (n^{lo{g}_{2}7})$

4.7 最近对问题

1）概述：最近对问题要求在一个包含n个点的集合中，找出距离最近的两个点$d(p_i,p_j)=\sqrt{(x_i-x_j{)}^2-(y_i-y_j{)}^2}$

2）算法：

当$2\le n\le 3$时，可以通过蛮力算法求解。

当$n\ge 3$时，利用点集在x轴方向上的中位数m，在该处做一条垂线，将点集分成大小分别为n/2和n/2的两个子集$P_1$和$P_r$，使得n/2个点位于线的左边或线上，n/2个点位于线的右边或线上，通过递归求解子问题$P_1$和$P_r$来得到最近点对问题的解，其中$d_1$和$d_r$分别表示在$P_1$和$P_r$中的最近对距离，并定义$d=min{d}_1,d_r$。

但d不一定是所有点对的最小距离，因为距离最近的两个点可能分别位于分界线的两侧，因此在合并较小子问题的解时，需要检查是否存在这样的点。

算法 EfficientClosestPair(P,Q)
//使用分治算法来求解最近点对问题
//输入：数组P中存储了平面上的n>=2个点，并且按照这些点的x轴坐标升序排列
//	   数组Q中存储了与P相同的点，只是它是按照这点的y轴坐标升序排列
//输出：最近点对之间的欧几里得距离
if n<=3
    返回由蛮力算法求出的最小距离
else 
    将P的前[n/2]个点复制到P1
    将Q的前[n/2]个点复制到Q1
    将P中余下的[n/2]个点复制到Pr
    将Q中余下的[n/2]个点复制到Qr
    d1 <- EfficientClosestPair(P1,Q1)
    dr <- EfficientClosestPair(Pr,Qr)  
    d  <- min(d1,dr)
    m  <- p[(n/2)-1].x
    将Q中所有|x-m|<d的点复制到数组S[0..num-1]
    dminsq <- pow(d,2)
    for i  <- 0 to num-1 do 
        k  <- i+1
        while k<=num-1 and pow((S[k].y-S[i].y),2)< dminsq
        	dminsq <- min(pow((S[k].x-S[i].x),2)+pow((S[k].y-S[i].y),2),dminsq)
            k <- k+1
return sqrt(dminsq)

3）时间复杂度：$\Omega (nlogn)$

4.8 凸包问题

1）概述：在平面或者高维空间的一个给定点集合中寻找凸包。

2）（快包算法）：

假设集合S由平面上n>1个点构成，假设这些点按照x轴坐标升序排列，如果x轴坐标相同，则按照y轴坐标升序排列。

直线$\overrightarrow{p_1{p}_n}$把点分为两个集合，$S_1$是位于直线左侧或直线上的点构成的集合，$S_2$是位于直线右侧或直线上的点构成的集合（如果$\overrightarrow{q_1{q}_2}$是方向从$q_1$到$q_2$的直线，如果$q_1{q}_2{q}_3$构成了一个逆时针回路，则说$q_3$位于$\overrightarrow{q_1{q}_2}$的左侧）

集合S由上包和下包构成；

构造上包

如果$S_1$为空，上包就是以$p_1$和$p_n$为端点的线段。

如果$S_1$不为空，该算法找到$S_1$中的顶点$p_{max}$,他是距离直线$\overrightarrow{p_1{p}_n}$最远的点，如果距离直线最远的点有多个，就找能使角$\angle p_{max}{p}_1{p}_n$最大的点，然后找出$S_1$中所有在直线$\overrightarrow{p_1{p}_{max}}$左边的点，这些点以及$p_1$和$p_{max}$构成了集合$S_{1，1}$，$S_1$中所有在直线$\overrightarrow{p_1{p}_{max}}$左边的点，这些点以及和$p_{max}$构成$p_n$了集合$S_{1，2}$。因此该算法可以继续递归构造$p_1\bigcup S_{1,1}\bigcup p_{max}$和$p_{max}\bigcup S_{1,2}\bigcup p_n$的上包，然后把它们连接起来，以得到整个集合$p_1\bigcup S_1\bigcup p_n$的上包

构造下包也同理

该算法的几何操作：

如果$q_1(x_1,x_1),q_2(x_2,x_2),q_3(x_3,x_3)$是平面上的任意三个点，那么三角形$\Delta q_1{q}_2{q}_3$的面积等于下列这个行列式绝对值的二分之一。

$\left|\begin{array}{ccc}{x}_1& y_1& 1\\ x_1& y_1& 1\\ x_1& y_1& 1\end{array}\right|=x_1{y}_2+x_3{y}_1+x_2{y}_3-x_3{y}_2-x_2{y}_1-x_1{y}_3$

当且仅当$q_3=(x_3,y_3)$位于直线$\overrightarrow{q_1{q}_2}$的左侧时，该表达式的符号为正。

3）时间复杂度：$\Theta (n^2)$

五、变治法

5.1 原理

5.1 预排序

5.1.1 思想

在计算机科学中，预排序是一种很古老的思想。实际上，对于排序算法的兴趣很大程度上是因为这样一个事实：如果列表是有序的，许多关于列表的问题更容易求解。

5.1.2 应用

1）检验数组元素的唯一性

先对数组排序，然后只检查他的连续元素

2）模式计算

在给定的数字列表中最经常出现的一个数值称为模式

如果若干个不同的值都是最经常出现的，他们中的任何一个值都可以看作模式

先对输入排序，这样所有相等的数值都会邻接在一起。要求出模式，只需求出在该有序数组中邻接次数最多的等值元素即可。

3）查找问题

如果给定的数组预先排好序，可以应用折半查找。

5.2 高斯消去法

5.2.1 原理

1）原理：

把n个线性方程构成的n元联立方程组变换为一个等价的方程组（也就是说，它的解和原来的方程组相同），该方程组有着一个上三角的系数矩阵，这种矩阵的主对角先下方元素全部为0。$Ax=b⟹A^{\prime }x=b^{\prime }$

通过初等变换将A推导出A‘

初等变换

交换方程组中两个方程的位置

把一个方程替换为它的非零倍

把一个方程替换为它和另一个方程倍数之间的和或差。

2）流程：

a. 前向消元：将系数矩阵变换为上三角形式，消除系数矩阵的下三角元素。

b. 回代：从最后一行开始，通过反向替换求解方程组的解。

3）实例：

4）伪代码：

注意:如果A[i，i]=0，就不能以他为除数

5）优化：部分选主元法

时间复杂度：$\Theta (n^3)$

5.2.2 LU分解

参考学习解线性方程组——直接解法：LU分解、PLU分解(类似列主元消去法) | 北太天元_lu直接分解-优快云博客

1）原理：把一个矩阵分成一个下三角矩阵乘上一个上三角矩阵的形式

2）实例：

$A=\left[\begin{array}{ccc}2& -1& 1\\ 4& 1& -1\\ 1& 1& 1\end{array}\right]$则有$L=\left[\begin{array}{ccc}1& 0& 0\\ 2& 1& 0\\ \frac{1}{2}& \frac{1}{2}& 1\end{array}\right]$，$U=\left[\begin{array}{ccc}2& -1& 1\\ 0& 3& -3\\ 0& 0& 2\end{array}\right]$

可以看出两个矩阵的乘积LU等于矩阵A，所以解方程组Ax=b等价于解方程组LUx=b。

设y=Ux，那么Ly=b。

$\left[\begin{array}{ccc}1& 0& 0\\ 2& 1& 0\\ \frac{1}{2}& \frac{1}{2}& 1\end{array}\right]\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right]=\left[\begin{array}{c}1\\ 5\\ 0\end{array}\right]$

则有$y_1=1,y_2=5-2y_1=3,y_3=0-\frac{1}{2}{y}_1-\frac{1}{2}{y}_2=-2$

解Ux=y意味着解

$\left[\begin{array}{ccc}2& -1& 1\\ 0& 3& -3\\ 0& 0& 2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}1\\ 3\\ -2\end{array}\right]$

而它的解是：

$x_3=(-2)/2=-1,x_2=(3-(-3)x_3)/3=0,x_1=(1-x_3-(-1)x_2)/2=1$

5.2.3 计算矩阵的逆

1）逆：一个n阶的方阵的逆也是一个n阶方阵，我们把它记作$A^{-1}$，使得$A{A}^{-1}=I$。其中I是一个单位矩阵

2）求解：参考学习逆矩阵 (shuxuele.com)

5.2.4 计算矩阵的行列式

1）行列式：一个n阶方阵A的行列式记作det A或者|A|。

2）计算：

如果n=1，$detA=a_{11}$

如果n>1，$detA={\sum }_{j=1}^n{s}_j{a}_{1j}det{A}_j$

3）实例：

4）克拉默法则：参考学习Cramer`s Rule 克莱姆法则（克拉默法则）-优快云博客

5.3 平衡查找树

5.3.1 原理

二叉查找树在平均情况下查找、插入和删除的时间效率都属于$\Theta (logn)$，但在最差情况下这些操作属于$\Theta (n)$，因此给出两种方案。

1）实例化简类型：

把一颗不平衡的二叉查找树转变为平衡的形式，这类树属于自平衡。特例有：AVL树，红黑树，分裂树。

2）改变表现类型：

允许一棵查找树的单个节点中不止包含一个元素。特例有：2-3树，2-3-4树以及B树。

5.3.2 AVL树

1）定义：

一颗AVL树是一颗二叉查找树，其中每个节点的平衡因子定义为该节点左子树和右子树的高度差，这个平衡因子要么为0，要么为+1或者-1（一颗空树的高度定义为-1，当然，平衡因子也可以被定义为左右子树的叶子数的差而不是高度差）

2）算法：如果插入的新节点是一颗AVL树失去了平衡，则用旋转对这棵树做一个变换。

4种旋转的简单形式：

5.3.3 2-3树

1）定义：

是一种可以包含两种类型节点的树：2节点和3节点。一个2节点只包含一个键K和两个子女：左子女作为一颗所有键都小于K的子树的根，而右子女作为一颗所有键都大于K的子树的根。一个3节点包含两个有序的键$K_1$和$K_2$（$K_1<K_2$)并且有3个子女。最左边的子女作为键值小于$K_1$的子树的根，中间的子女作为键值位于$K_1$和$K_2$之间的子树的根，最右边的子女作为一颗键值大于$K_2$的子树的根。

2-3树要求树中的所有叶子必须位于同一层，即是说一颗2-3树总是高度平衡的。

2）算法：

参考学习2-3树 - 算法与复杂度 | 小白·菜的空间 (infinityglow.github.io)

查找：

（1）如果根是一个2节点，如果K等于根的键值，算法停止；如果K小于或大于根的键值，分别在左子树或右子树中继续查找。

（2）如果根是一个3节点，在不超过两次比较之后，就能知道是停止查找（K等于根的某个键值），还是应该在根的3课子树的哪一棵中继续查找。

插入：

排除空树，否则我们总是把一个新的键K插入一个叶子里。

通过查找K来确定一个合适的插入位置，如果找到的叶子是一个2节点，根据K是小于还是大于节点中原来的键，把K作为第一个键或者第二个键插入。如果叶子是一个3节点，则把叶子分裂成2个节点：3个键（2个原来的键和1个新键）中最小的放到第一个叶子中，最大的键放到第二个叶子中，同时中间的键提升到原来父母中（如果这个叶子恰好是树的根，就创建一个新的根来接纳这个中间键）注意，中间键提升到父母中可能会导致父母的溢出（如果她是一个3节点）并且因此会导致 沿着该叶子的祖先链条发生多个节点的分裂。

3）时间复杂度：$\Theta (logn)$

5.4 堆和堆排序

可参考学习07. 堆排序 | 算法通关手册（LeetCode） (itcharge.cn)

5.4.1 堆

这里主要讨论大根堆

1）堆：

堆可以定义为一棵二叉树，树的节点中包含键（每个节点一个键），并且满足下面的两个条件：

(1)树的形状——这棵树是基本完备的，简称为完全二叉树

(2)父母优势——每个节点的键都要大于或等于他子女的键

2）特性：

• 只存在一颗n个节点的完全二叉树，它的高度为$lo{g}_{2}n$
• 堆的根总是包含了堆的最大元素
• 可以用数组来实现堆，方法使用从上到下、从左到右的方式来记录堆的元素。为了方便，可以在数组从1到n的位置上存放堆元素，留下H[0]。那么则有父母节点的键将位于前n/2个位置中，而叶子节点的键将占据后n/2个位置。

因此也可以把堆定义为一个数组H[1…n]，其中数组前半部分中，每个位置i上的元素总是大于等于位置2i和2i+1中的元素，即$对于i=1，\cdots \lfloor n/2\rfloor ,H[i]\ge maxH[2i],H[2i+1]$

3）构造：

自底向上堆构造

（1）按照给定的顺序来放置键

（2）从最后的父母节点开始，到根为止，检查节点的键是否满足父母优势要求，如果不满足，把节点的键K和它子女的最大键进行交换

（3）在新位置上检查K是否满足父母优势要求，直到对K的父母优势要求得到满足

自顶向下堆构造

时间效率为O(logn)

4）删除：

（1）根的键和堆的最后一个键K做交换

（2）堆的规模减1

（3）严格按照自底向上堆构造算法，把K沿着树向下帅选，来对这颗较小的树进行堆化

5.4.2 堆排序

1）流程

（1）构造堆，即为一个给定的数组构造一个堆

（2）删除最大键，即对剩下的堆应用n-1次根删除操作

2）时间复杂度：$O(nlogn)$

5.5 霍纳法则

1）介绍：一个古老的计算多项式的算法，但却十分优雅和高效。

2）算法：

已知x，求多项式$p(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0$ (6.1)

由式(6.1)推导

$p(x)=(\cdots (a_{n}x+a_{n-1})x+\cdots )x+a_0$ (6.2)

a. 实例

对于多项式$p(x)=2x^4-x^3-3x^2+x-5$ ，则有

$p(x)=2x^4-x^3-3x^2+x-5=x(2x^3-x^2+3x+1)-5=x(x(2x^2-x+3)+1)-5=x(x(x(2x-1)+3)+1)-5$ (6.3)

当x=3时

系数	2	-1	3	1	-5
x=3	2	$3\times 2+(-1)=5$	$3\times 5+3=18$	$3\times 18+1=55$	$3\times 55+(-5)=160$

所以p(3)=160

b. 伪代码

算法 Horner(P[0..n],x)
	//用霍纳法则求一个多项式在一个给定点的值
	//输入：一个n次多项式的系数数组P[0..n]（从低到高存储），以及一个数字x
	//输出：多项式在x点的值
	p <- P[n]
	for i <- n-1 downto 0 do
		p <- x*p+P[i]
    return p

3）时间复杂度： $\Theta (n)$

5.6 二进制幂

1）介绍：当用霍纳法则计算$a^n$时，退化成了一种对a自乘的蛮力算法。

2）算法

设$n=b_l\cdots b_i\cdots b_0$是在二进制系统中，表示一个正整数n的位串。这意味着可以通过下面的式子来计算n的值

$p(x)=b_l{x}^l+\cdots +b_i{x}^i+\cdots +b_0$，其中x=2。

实例：如果n=13，他的二进制表示是1101，就有$13=1\times 2^3+1\times 2^2+0\times 2^1+1\times 2^0$

从左至右二进制幂

有$a^n=a^{p(2)}=a^{b_l{x}^l+\cdots +b_i{x}^i+\cdots +b_0}$

用霍纳法则计算p(2)，就有：

$a^{2p+b_i}=a^{2p}\times a^{b_i}=(a^p{)}^2\times a^{b_i}=\{\begin{array}{ll}(a^p{)}^2& 如果b_i=0\\ (a^p{)}^2\times a& 如果b_i=1\end{array}$

实例：

从右至左二进制幂

有$a^n=a^{p(2)}=a^{b_l{x}^l+\cdots +b_i{x}^i+\cdots +b_0}=a^{b_l{2}^l}\times \cdots \times a^{b_i{2}^i}\times \cdots \times a^{b_0}$

各项有：$a^{b_i{2}^i}=\{\begin{array}{ll}{a}^{2^i}& 如果b_i=1\\ 1& 如果b_i=0\end{array}$

实例：

5.7 问题化简

5.7.1 原理

5.7.2 求最小公倍数

1）介绍：两个正整数m和n的最小公倍数，记作lcm(m,n)，把它定义为能够被m和n整除的最小整数。

2）算法：$lcm(m,n)=\frac{m\times n}{gcd(m,n)}$，其中gcd(m,n)可以用欧几里得算法高效地计算出来欧几里得算法_百度百科 (baidu.com)

5.7.3 线性规划

线性规划（运筹学术语）_百度百科 (baidu.com)

六、时空权衡

6.1 原理

对问题的部分或全部输入做预处理，然后将获得的额外信息进行存储，以加速后面问题的求解，将这个方法称之为输入增强。

还有一种和空间换时间权衡思想相关的算法设计技术：动态规划。这个策略的基础是把给定问题中重复子问题的解记录在表中，然后求得所讨论问题的解。

注意：不是在所有的情况下，时间和空间这两种资源都必须相互竞争，实际上，它们可以联合起来，使得一个算法无论在运行时间上还是在消耗的空间上都达到最小化。

6.2 计数排序

可参考学习08. 计数排序 | 算法通关手册（LeetCode） (itcharge.cn)

6.2.1 比较计数排序

1）思想：针对待排序列表中的每一个元素，算出列表中小于该元素的元素个数，并把结果记录在一张表中。这个个数指出了该元素在有序列表中的位置。

2）算法：

算法 ComparisonCountingSort(A[0..n-1])
	//用比较计数法对数组排序
	//输入：可排序数组A[0..n-1]
	//输出：将A中元素按照升序排列的数组S[0..n-1]
	for i <- 0 to n-1 do Count[i] <- 0
	for i <- 0 to n-2 do 
		for j <- i+1 to n-1 do
			if A[i]<A[j]
				Count[j] <- Count[j]+1
		    else Count[i] <- Count[i]+1
		for i <- 0 to n-1 do S[Count[i]] <- A[i]
	return S

6.2.2 计数排序

1）思想：通过统计数组中每个元素在数组中出现的次数，根据这些统计信息将数组元素有序的放置到正确位置，从而达到排序的目的。

2）时间复杂度：$O(n+k)$,其中k代表待排序数据的值域大小

6.3 字符串匹配的输入增强技术

6.3.1 Horspool算法

1）原理

从模式的最后一个字符开始从右向左，比较模式和文本中的相应字符对。如果模式中所有的字符都匹配成功，就找到了一个匹配的子串，就可以结束查找。如果遇到了一对不匹配字符，需要把模式右移。

假设文本中，对齐模式最后一个字符的元素是字符c，Horspool算法根据c的不同情况来确定移动的距离，无论c是否和模式的最后一个字符相匹配。

😄会有以下4种情况：

（1）如果模式中不存在c，模式安全移动的幅度就是他的全部长度。

（2）如果模式存在c，但它不是模式的最后一个字符，移动时应该把模式中最右边的c和文本中的c对齐

（3）如果c正好是模式中的最后一个字符，但是在模式的其他m-1个字符中不包含c，移动的情况就是类似（1）

（4）如果c正好是模式中的最后一个字符，且在模式的其他m-1个字符中也包含c，移动的情况就类似于（2）

🍰移动距离$t(c)=\{\begin{array}{ll}模式的长度m& 如果c不包含在模式的m-1个字符中\\ 模式前m-1个字符中最右边的c到模式最后一个字符的距离& 其他情况下\end{array}$（7.1）

2）实例

3）算法

算法 ShiftTable(P[0..m-1])
	//用Horspool算法和Boyer-Moore算法填充移动表
    //输入：模式P[0..m-1]以及一个可能出现字符的字母表
    //输出：以字母表中字符为索引的数组Table[0..size-1]
    //表中填充的移动距离是通过移动距离公式计算
    for i <- 0 to size-1 do Table[i] <- m
    for j <- 0 to m-2 do Table[P[j]] <- m-1-j   //该字符到模式右端的距离
    return Table
算法 HorspoolMatching(P[0..m-1]，T[0..n-1])
    //实现Horspool字符串匹配算法
    //输入：模式P[0..m-1]和文本T[0..n-1]
    //输出：第一个匹配子串最左端字符的下标，如果没有匹配子串，则返回-1
    ShiftTable(P[0..m-1])                  //生成移动表
    i <- m-1							   //模式最右端
    while i<=n-1 do						   
        k <- 0							   //匹配字符串个数
        while k<=m-1 and P[m-1-k]=T[i-k] do 
            k <- k+1
        if k=m
        	return i-m+1
        else i <- i+Table[T[i]]
    return -1

🍎最差效率：O(nm)

☔️对于随机文本：$\Theta (n)$

6.3.2 Boyer-Moore算法

1）原理

如果模式最右边的字符和文本中的相应字符c所做的初次比较失败了，该算法和Horspool算法所做的操作完全一致。

然而在遇到一个不匹配字符之前，如果已经有k(0<k<m)个字符成功匹配，这两个算法的操作是不同的。

在这种情况下，Boyer-Moore算法会参考两个数值来确定移动的距离：第一个数值是由文本中的一个字符c确定的，它导致了模式中的相应字符和它不匹配，因此称为坏符号移动。可以用$t_1(c)-k$来计算移动的距离，其中$t_1(c)$是Horspool算法用到的预先算好的表中的单元格，而k是成功匹配的字符串个数。

😄坏符号移动 d 1 = m a x { t 1 c − k , 1 } d_1=max\lbrace t_1c-k,1\rbrace d1​=max{t1​c−k,1}，如果$d_1$>0，为$t_1(c)-k$，否则则为1。

第二种移动是由模式中最后k>0个成功匹配的字符确定的。把模式的结尾部分叫做模式的长度为k的后辍，记作suff(k)，把这种类型称为好后辍移动。好后辍移动表是根据模式后辍的长度1，…，m-1来分别填充表格的。$d_2$是从右数第二个suff(k)到最右边的suff(k)之间的距离。

2）流程：

3）时间复杂度：最坏情况下是线性的。

4）实例

6.4 散列法

6.4.1 思想

1）思想

把键分布在一个称为散列表的一维数组H[0…m-1]中，通过对每个键计算某些被称为散列函数的预定义函数h的值，来完成这种分布。该函数为每个键指定一个称为散列地址的位于0到m-1之间的整数。

2）特点

散列函数需要满足下列要求

（1）散列表的长度相对于键的个数不应过大，但也不应过小

（2）散列函数需要把键在散列表的单元格中尽可能均匀分布

（3）散列函数必须容易计算

如果散列表长度m小于键的数量n，会遇到碰撞

6.4.2 开散列（分离链）

1）思想：键被存储在附着于散列表单元格上的链表中。

2）实例：假设使用用于字符串的简单函数来作为散列函数，即将词中的字母在字母表中的位置全部加起来，在除以13以后，计算出这个和的余数，这就是散列表的长度。

查找：设要查找键KID，先算出h(KID)=11，发现附着在单元格11上的链表不为空：先把KID与ARE比较，然后与SOON比较之后，才以失败告终。

如果散列函数大致均匀将n个键分布在散列表的m个单元格中，每个链表长度大约为n/m个键，其比率a=n/m称为散列表的负载因子。假设在成功查找和不成功查找中平均需检查的指针个数分别为S和U，他们的值分别为：$S=1+\frac{a}{2},U=a$

6.4.3 闭散列（开式寻址）

1）思想：所有的键都存储在散列表本身中，而没有使用链表。可采用不同的策略来解决碰撞：线性探查，它检查碰撞发生处后面的单元格，如果该单元格为空，新的键就放置在那里；如果该单元格被占用，则检查该单元格的后继是否可用，以此类推，如果到达了散列表的尾部，就折回到表的开始处。

2）实例：

查找：设要查找键KID，先算出h(KID)=11，如果单元格为空，则查找失败，如果单元格不为空，则将其与单元格的内容进行比较，如果相等，就找到了一个匹配的键；如果不相等，就拿键KID与下一个单元格中的键比较，直到遇到一个匹配的键或一个空的单元格。

在成功查找和不成功查找的情况下，对于负载因子为a的散列表，该算法要访问的次数分别为：$S\approx \frac{1}{2}(1+\frac{1}{1-a})$和$U\approx \frac{1}{2}[1+\frac{1}{(1-a{)}^2}]$

线性探查中的聚类是一系列被连续占据的单元格（包括可能的环绕），聚类对于散列是一个坏消息，因为他们降低了字典操作的效率。

6.5 B树

1）思想：所有的数据记录（或者记录的键）都按照键的升序存储在叶子中，他们的父母节点作为索引。每个父母节点包含n-1个有序的键$K_1<\cdots <K_{n-1}$，子树$T_0$中的所有键都小于$K_1$，子树$T_1$中的所有键都大于等于$K_1$且小于$K_2$

2）特性

对于一颗次数为$m\ge 2$的B树要满足以下特性：

• 它的根要么是一个叶子，要么具有2到m个子女
• 除了根和叶子以外的每个节点，具有m/2到m个子女
• 这棵树是完美平衡的，也就是说他的所有叶子都在同一层上

2）算法：

查找：和二叉查找树的查找非常相似，时间效率为O(logn)

插入：和2-3树插入算法非常相似。

七、动态规划

7.1 原理

动态规划是一种算法设计技术，有着相当有趣的历史，是一种是多阶段决策过程最优的通用方法。

7.1 背包问题

1）概述：给定n个重量为$w_1,w_2,\dots \dots w_n$,价值为$v_1,v_2,\dots \dots ,v_n$的物品和一个承重为W的背包，求这些物品中一个最有价值的子集，并且要能够装到背包中。

2）算法：

设F(i,j)为该实例的最优解的物品总价值，背包的承重量为j，物品的重量分别为$w_1,\cdots w_i$，价值分别为

$v_1,\cdots v_i$；则有

（1）在不包括第i个物品的子集中，最优子集的价值是F(i-1,j)

（2）在包括第i个物品的子集中，最优子集是由该物品和前i-1个物品中能够放进承重量$j-w_i$的背包的最优子集组成，这种最优子集的总价值为$v_i+F(i-1,j-w_i)$。

😄 F ( i , j ) = { m a x { F ( i − 1 , j ) , v i + F ( i − 1 , j − w i ) } , j − w i ≥ 0 F ( i − 1 , j ) , j − w i < 0 F(i,j)=\begin{cases} max\lbrace F(i-1,j),v_i+F(i-1,j-w_i)\rbrace, & \text j-w_i \geq 0 \\[4ex] F(i-1,j), & \text j-w_i<0 \end{cases} F(i,j)=⎩ ⎨ ⎧​max{F(i−1,j),vi​+F(i−1,j−wi​)},F(i−1,j),​j−wi​≥0j−wi​<0​

​ 当$j\ge 0时，F(0,j)=0;当i\ge 0时，F(i,0)=0$

3）实例：

7.2 最优二叉查找树

1）思想：设$a_1,\cdots ,a_n$是从小到大排列的互不相等的键，$p_1,\cdots ,p_n$是他们的查找概率。$T_i^j$是由键$a_i,\cdots ,a_j$构成的二叉树，C(i,j)是这棵树中成功查找的最小平均查找次数，其中i，j是一些整数的下标。从键$a_i,\cdots ,a_j$中选择一个根$a_k$，使得他的左子树最优排列，右子树最优排列。

当 1 ≤ i ≤ j ≤ n 时 , C ( i , j ) = m i n i ≤ k ≤ j m i n { C ( i , k − 1 ) + C ( k + 1 , j ) } + ∑ s = i j p s 1 \leq i \leq j\leq n时,C(i,j)=min_{i\leq k\leq j} min\lbrace C(i,k-1)+C(k+1,j)\rbrace +\sum ^j_{s=i}p_s 1≤i≤j≤n时,C(i,j)=mini≤k≤j​min{C(i,k−1)+C(k+1,j)}+∑s=ij​ps​

当$1\le i\le n时,C(i,i)=p_i$

当$1\le i\le n+1时,C(i,i-1)=0$

2）实例：

2）算法：

算法 OptimalBST(P[1..n])
    //用动态规划算法求最优二叉查找树
    //输入：一个n个键的有序列表的查找概率数组P[1..n]
    //输出：在最优BST中成功查找的平均比较次数，以及最优BST中子树的根表R
    for i <- 1 to n do 
        C[i,i-1] <- 0
        C[i,i] <- P[i]
        R[i,i] <- i
    C[n+1,n] <- 0
    for d  <- to n-1 do //对角数计数
        for i <- 1 to n-d do 
            j <- i+d
            minval <- 无穷
            for k <- i to j do 
                if C[i,k-1]+C[k+1,j]<minval
                minval <- C[i,k-1]+C[k+1,j];kmin <- k
             R[i,j] <- kmin
             sum <- P[i];for s  <- i+1 to j do sum <- sum+P[s]
             C[i,j] <- minval+sum
     return C[1,n],R

3）时间复杂度：立方级

7.3 Warshell算法

1）思想：

😢定义：一个n顶点有向图的传递闭包可以定义为一个n阶布尔矩阵 T = { t i j } T=\lbrace t_{ij} \rbrace T={tij​}，如果从第i个顶点到第j个顶点之间存在一条有效的有向路径（即长度大于0的有向路径），矩阵第i行第j列的元素为1，否则为0。

假设有向图的顶点数目为n，因此顶点矩阵的行和列可以用1到n表示，Warshell算法通过一系列n阶布尔矩阵来构造传递闭包。$R^{(0)},\cdots ,R^{(k-1)},R^{(k)},R^{(n)}$ (8.9)

Warshell算法核心是任何$R^{(k)}$中的所有元素都可以通过它在序列(8.9)中的直接前趋$R^{(k-1)}$计算得到。把矩阵$R^{(k)}$中第i行第j列的元素$r_{ij}^{(k)}$置为1。意味着存在一条从第i个顶点$v_i$到第j个顶点$v_j$的路径，路径中每一个中间顶点的编号都不大于k。

​ $r_{ij}^{(k)}=r_{ij}^{(k-1)}或r_{ik}^{(k-1)}和r_{kj}^{(k-1)}$

2）实例：

3）算法：

时间复杂度：$\Theta (n^3)$

7.4 Floyd算法

1）思想：给定一个加权连通图（无向的或有向的），安全最短路径问题要求找到从每个顶点到其他所有顶点之间的距离（最短路径长度）。把最短路径的长度记录在距离矩阵的n阶矩阵D中：矩阵第i行第j列的元素$d_{ij}$指出了从第i个顶点到第

j个顶点之间最短路径的长度$(1\le i,j\le n)$。可以采用一种类似于Warshell算法来生成距离矩阵。

Floyd算法通过一系列n阶矩阵来计算一个n顶点加权图的距离矩阵：$D^{(0)},\cdots ,D^{(k-1)},D^{(k)},\cdots ,D^{(0)},$

​ 当 k ≥ 1 , d i j ( 0 ) = w i j 时， d i j ( k ) = m i n { d i j ( k − 1 ) , d i k ( k − 1 ) + d k j ( k − 1 ) } k \geq 1,d_{ij}^{(0)}=w_{ij}时，d_{ij}^{(k)}=min \lbrace d_{ij}^{(k-1)},d_{ik}^{(k-1)}+d_{kj}^{(k-1)}\rbrace k≥1,dij(0)​=wij​时，dij(k)​=min{dij(k−1)​,dik(k−1)​+dkj(k−1)​}

2）实例：

3）算法：

算法 Floyd(W[1..n,1..n])
    //实现计算完全最短路径的Floyd算法
    //输入：不包含长度为负的回路的图的权重矩阵W
    //输出：包含最短路径长度的距离矩阵
    D <- W              //如果可以改写W，这一步可以省略
    for k <- 1 to n do
        for i <- 1 to n do
            for j <- 1 to n do 
                D[i,j] <- min{D[i,j],D[i,k]+D[k,j]}
    return D

时间复杂度：$\Theta (n^3)$

八、贪婪技术

8.1 原理

通过一系列步骤来构造问题的解，每一步对目前构造的部分解做一个拓展，直到获得问题的完整解为止。这个技术的核心是，所做的每一步选择都必须满足以下条件：

（1）可行性：即它必须满足问题的约束

（2）局部最优：是当前步骤所有可行选择中最佳的局部选择

（3）不可取消：选择一旦做出，在算法的后面步骤中就无法改变了。

8.2最小生成树问题

8.2.1 Prim算法

参考学习最小生成树 - OI Wiki (oi-wiki.org)

1）思想：

定义：连通图的一颗生成树是包含图的所有顶点的连通无环子图（也就是一棵树）。加权连通图的一棵最小生成树是图的一棵权重最小的生成树，其中，树的权重定义为所有边的权重总和。最小生成树问题就是求一个给定的加权连通图的最小生成树问题。

Prim算法通过一系列不断扩张的子树来构造一棵最小生成树。从图的顶点集合V中任意选择一个单顶点，作为序列中的初始子树。每一次迭代以一种贪婪的方式来扩张当前的生成树，即把不在树中的最近顶点添加到树中。当图的所有顶点都包含在所构造的树中以后，该算法就停止了。

2）算法：

3）时间复杂度：$O(|E|log|V|)$

8.2.2 Kruskal算法

😄参考学习最小生成树 - OI Wiki (oi-wiki.org)

1）思想：将一个加权连通图G=<V,E>的最小生成树看作一个具有|V|-1条边的无环子图，并且边的权重和是最小的。

该算法开始时，会按照权重的非递减顺序对图的边进行排序，然后从一个空子图开始，扫描这个有序列表，并试图把列表中的下一条边加到当前的子图中，如果产生了回路，则把这条边跳过。

2）算法：

3）时间复杂度：假如排序算法是高效的：$O(|E|log|E|)$

8.3 Dijkstra算法

参考学习[最短路径问题]Dijkstra算法(含还原具体路径) - MarisaMagic - 博客园 (cnblogs.com)

1）思想：

单起点最短路径问题：对于加权连通图的一个称为起点的给定顶点，求出它到所有其他顶点之间的一系列最短路径。

Dijkstra算法按照从给定起点到图中顶点的距离，顺序求出最短的路径。首先求出从起点到最接近起点的顶点之间的最短路径，然后求出第二近的，以此类推。

2）实例：

3）算法：

8.4 哈夫曼树及编码

参考学习霍夫曼树 - OI Wiki (oi-wiki.org)

1）思想：

假设必须为文本中的每一个字符赋予一串称为代码字的比特位，对n个不同字符组成的文本进行编码，并且这些字符都来自于某张字母表。

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

哈夫曼树最重要的应用是哈夫曼编码

2）算法：

🦀哈夫曼算法：

（1）初始化n个单节点的树，并为他们标上字母表中的字符。把每个字符的概率记在树的根中，用来指出树的权重（树的权重等于树中所有叶子的概率之和）

（2）重复以下步骤，直到只剩一颗单独的树。找到两棵权重最小的树（对于权重相同的树，可任选其一）。把它们作为新树中的左右子树，并把其权重之和作为新的权重记录在新树的根中。

🦀哈夫曼编码：

一种最优的自由前缀变长编码方案，基于字符在给定文本中的出现频率，把位串赋给字符。这是通过贪婪地构造一棵二叉树来完成的，二叉树的叶子代表字母表中的字符，而树中的边则标记为0或1。

3）实例：