机器学习——支持向量机（SVM）

栀沫-x

已于 2024-06-11 16:47:17 修改

阅读量7.8k

点赞数 29

文章标签：支持向量机机器学习算法

于 2024-06-11 16:36:41 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_74731967/article/details/139598635

版权

一、SVM介绍

1.1SVM基本概念

        支持向量机（Support Vector Machine，SVM）是一种常用的机器学习算法，SVM可以用于线性和非线性分类问题，回归以及异常值检测
        其基本原理是通过在特征空间中找到一个超平面，将不同类别的样本分开，并且使得离超平面最近的样本点到超平面的距离最大化。这个超平面称为最大间隔超平面，它可以很好地进行分类预测。
        具体而言，SVM通过将样本映射到高维特征空间，使得数据在该空间中线性可分。如果在原始输入空间中无法找到一个线性超平面将数据分开，SVM引入了核函数，将计算复杂度从高维特征空间转移到原始输入空间中。常用的核函数有线性核、多项式核和高斯核等。

1.2线性可分支持向量

D0 和 D1 是 n 维欧氏空间中的两个点集。如果存在 n 维向量 w 和实数 b，使得所有属于 D0 的点Xi都有 wXi+b>0 ，而对于所有属于 D1 的点则有 wXi+b<0 ，则称 D0 和 D1 线性可分。

如图：两类点被一条直线完全分开叫做线性可分。

1.3最大间隔超平面

分割直线可能不止一条，为了保证鲁棒性，将会选择中间的一条直线。

鲁棒性是指系统或算法对于输入数据发生变化或异常情况时的稳定性和可靠性。一个鲁棒性强的系统能够在面对不同类型的输入数据时仍能保持良好的表现，并且能够有效地处理异常情况，而不会产生严重的错误或崩溃。

从二维扩展到多维空间中时，将 D0 和 D1 完全正确地划分开的 wx+b=0 就成了一个超平面。（w是权重，b是截距，训练数据就是训练得到权重和截距。）

为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。

两类样本分别分割在该超平面的两侧；

两侧距离超平面最近的样本点到超平面的距离被最大化了。

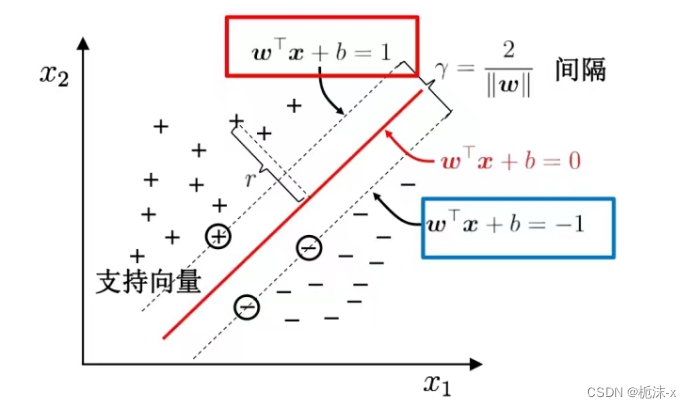
支持向量：样本中距离超平面最近的一些点，这些点叫做支持向量。

1.4软间隔和硬间隔

软间隔和硬间隔用于描述分类器对数据的容忍程度和灵活性。

硬间隔：在一个线性可分的情况下，硬间隔SVM试图找到一个能够完全将不同类别的数据分开的超平面。这意味着不允许任何数据点出现在间隔边界之间。硬间隔SVM对异常值非常敏感，因为即使一个异常值的存在都可能导致无法找到一个完全将数据分开的超平面。

软间隔：在实际应用中，数据往往不是完全线性可分的，可能会存在一些噪声或异常点。软间隔SVM允许一些数据点出现在间隔边界之间，并引入了超参数 C(惩罚系数），控制了模型的复杂度和容错能力。较小的C值会导致容错能力较高（即更宽的缓冲区），可能会产生更多的错误分类（即间隔违规）；较大的C值会导致容错能力较低，可能会产生更少的错误分类。

这样一来，软间隔SVM相对于硬间隔SVM具有更强的鲁棒性，能够更好地处理现实世界中的数据集。在实际应用中，软间隔SVM通常比硬间隔SVM更加常见，因为它能够更好地适应真实世界中的数据，对噪声和异常点有更好的容忍度。

以一个二维平面为例，判定边界是一个超平面（在二维平面是一条线），它是由支持向量所确定的（支持向量决定了判定边界的位置）。
间隔的正中就是判定边界，间隔距离体现了两类数据的差异大小