【蓝桥杯】壁画

Thanh 想在一面被均分为 N 段的墙上画一幅精美的壁画。每段墙面都有一个美观评分，这表示它的美观程度（如果它的上面有画的话）。不幸的是，由于洪水泛滥，墙体开始崩溃，所以他需要加快他的作画进度！每天 Thanh 可以绘制一段墙体。在第一天，他可以自由的选择任意一段墙面进行绘制。

在接下来的每一天，他只能选择与绘制完成的墙面相邻的墙段进行作画，因为他不想分开壁画。

在每天结束时，一段未被涂颜料的墙将被摧毁（Thanh 使用的是防水涂料，因此涂漆的部分不能被破坏），且被毁掉的墙段一定只与一段还未被毁掉的墙面相邻。

Thanh 的壁画的总体美观程度将等于他作画的所有墙段的美观评分的总和。Thanh想要保证，无论墙壁是如何被摧毁的，他都可以达到至少 B的美观总分。

请问他能够保证达到的美观总分 B 的最大值是多少。

输入格式

第一行包含整数 T，表示共有 T组测试数据。

每组数据的第一行包含整数 N。

第二行包含一个长度为 N的字符串，字符串由数字 0∼90∼9 构成，第 i个字符表示第 i段墙面被上色后能达到的美观评分。

输出格式

每组数据输出一个结果，每个结果占一行。

结果表示为 Case #x: y，其中 x为组别编号（从 11 开始），y为 Thanh 可以保证达到的美观评分的最大值。

数据范围

1≤T≤100
存在一个测试点N=5*10e6,其他测试点均满足2≤N≤100

输入样例：

4
4
1332
4
9583
3
616
10
1029384756

输出样例：

Case #1: 6
Case #2: 14
Case #3: 7
Case #4: 31

样例解释

在第一个样例中，无论墙壁如何被破坏，Thanh都可以获得 66 分的美观总分。在第一天，他可以随便选一个美观评分3的墙段进行绘画。在一天结束时，第一部分或第四部分将被摧毁，但无论哪一部分都无关紧要。在第二天，他都可以在另一段美观评分 33 的墙段上作画。

在第二个样例中，Thanh 在第一天选择最左边的美观评分为 99 的墙段上作画。在第一天结束时唯一可以被毁掉的墙体是最右边的那段墙体，因为最左边的墙壁被涂上了颜料。在第二天，他可以选择在左数第二段评分为 55 的墙面上作画。然后右数第二段墙体被摧毁。请注意，在第二天，Thanh不能选择绘制第三段墙面，因为它不与任何其他作画墙面相邻。这样可以获得 1414 分的美观总分。

思路：

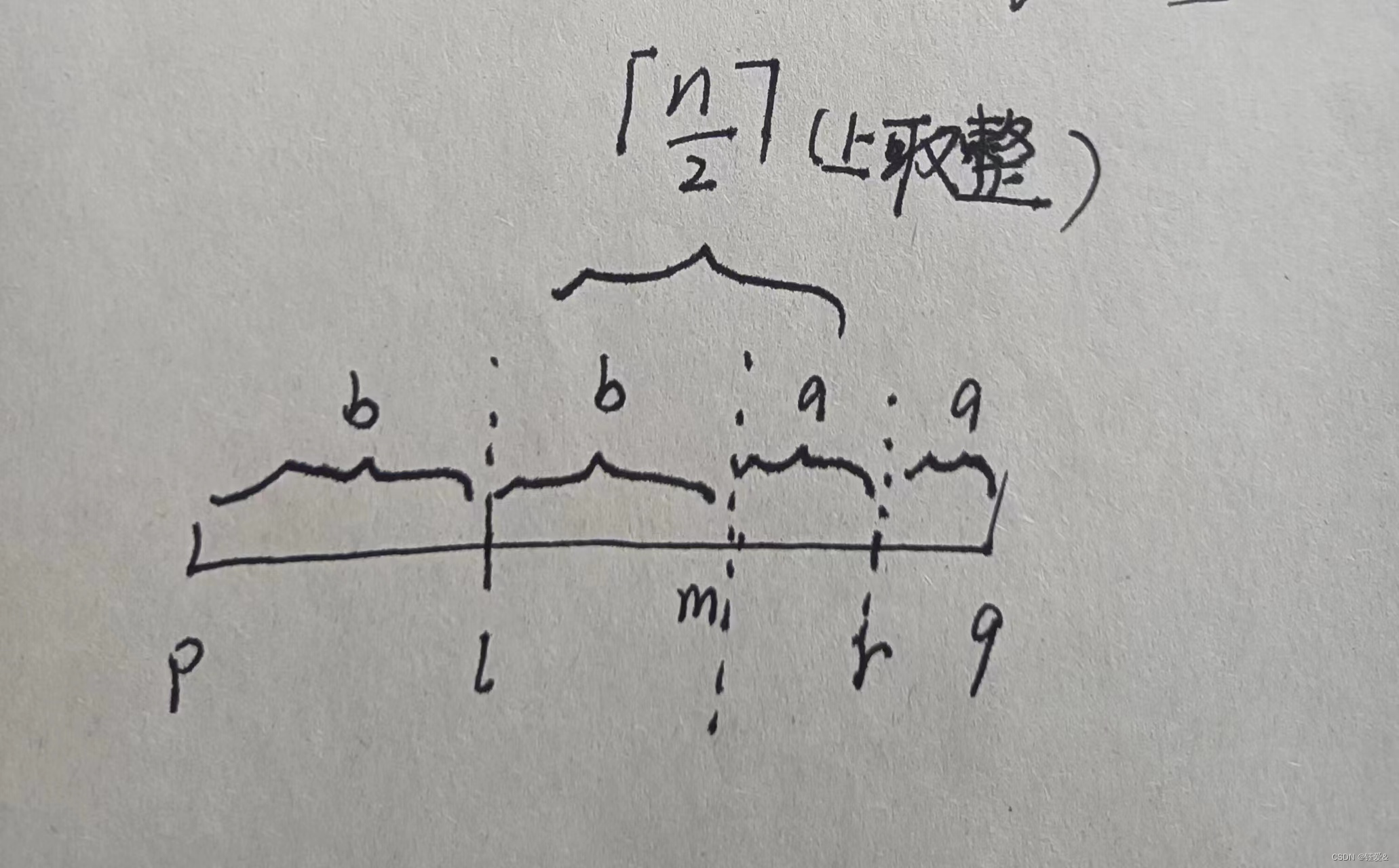
因为是先刷墙，后毁墙，所以如果为奇数，会多刷一面墙，上取整，最后会刷n/2或n/2+1，毁掉n/2

假设一整段为墙壁，任取n/2段（l,r）,以r为对称轴，q对称点为m，左边以l为中点，基本也是对称的

#include<iostream>
#include<algorithm>
#define N 5000010
using namespace std;
int main(){
    int n;
    int sum[N];
    char str[N];
    int t;
    cin>>t;
    for(int i=1;i<=t;i++){
        cin>>n;
        cin>>str+1;//从第1个开始存
        for(int j=1;j<=n;j++){//前缀和，最好序列从1开始
            sum[j]=sum[j-1]+str[j]-'0';//字符串转化为数字
        }
        int res=0,m=(n+1)/2;
        for(int k=m;k<=n;k++){
             res=max(res,sum[k]-sum[k-m]);//n/2的区间从头向右移动   
        }
        cout<<"Case #"<<i<<": "<<res<<endl;
    }
    return 0;
}