LeetCode题号96——不同的二叉搜索树（递归和动态规划两种解法，C++版本）

声明：原创代码，转载请附上本文链接

题目：

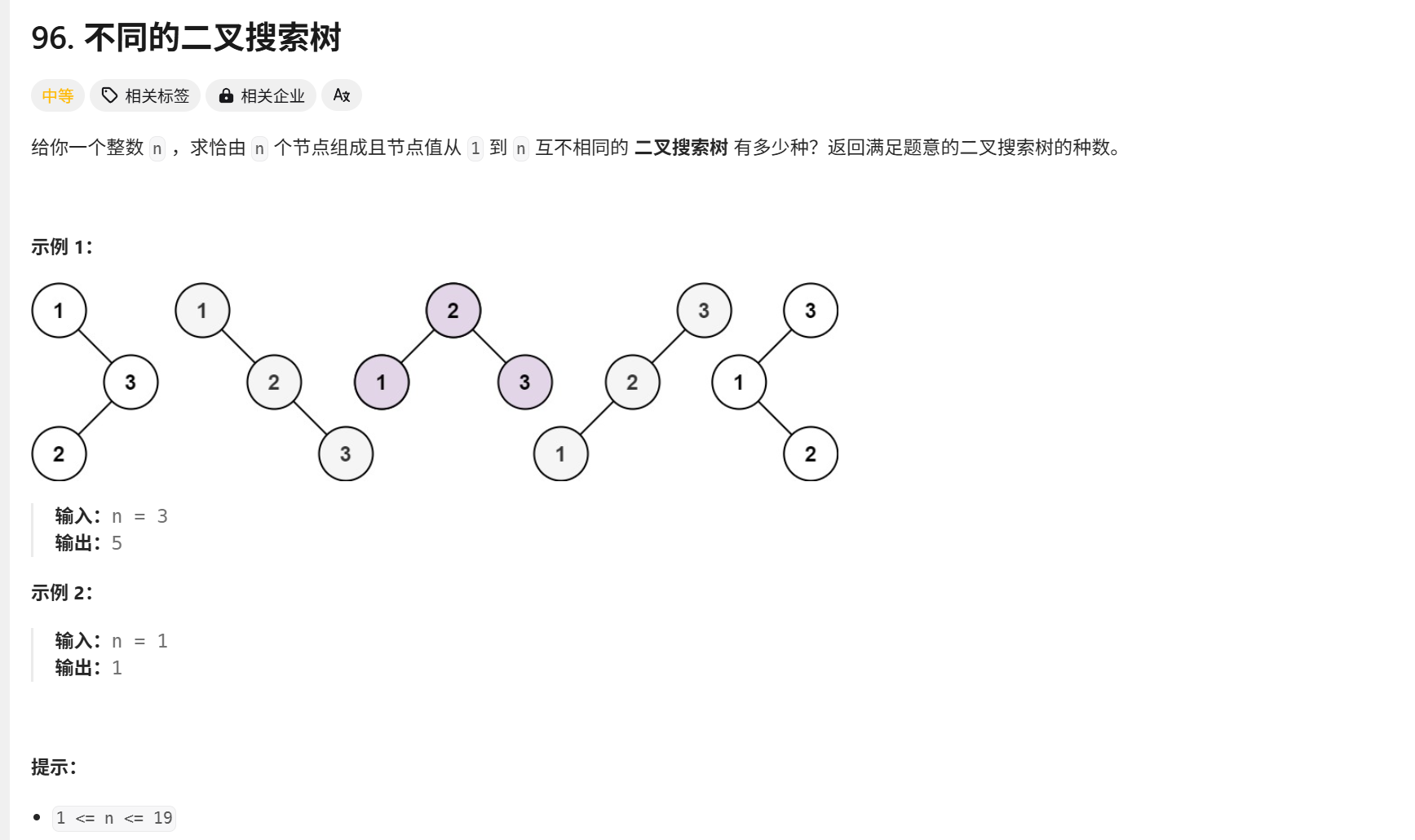
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

题目分析：

二叉搜索树（BST）是一种特殊的二叉树，满足以下性质：

• 每个节点的值大于其左子树中所有节点的值。

• 每个节点的值小于其右子树中所有节点的值。

题目要求计算由n个节点（值分别为1到n）组成的BST的种数。

该题完全等价于有n个不同节点值不同的节点，所能组成的二叉搜索树有多少分种？

思路分析：

这个题目主要有两种解法，分别是递归（暴力）和动态规划。、

首先讲解递归方法，递归也就是暴力算法，通过枚举每个节点作为根节点，然后进一步递归构造左右子树来求解该问题。该算法时间复杂度很高O(n^2)，在节点数较多的情况下算法效率较低，但理解起来非常直观，适合刚入门的小伙伴。基本思路就是：已经拥有一个递增的有序序列，通过遍历序列，将每个节点作为根节点进行BST构造，由于BST本身的特性，左子树的所有节点均比根节点小，右子树的所有结点均比根节点大，由于我们本身的节点序列已经是递增的，那么我们可以很直观的发现，当选取某个节点作为根节点构造BST时，该节点左侧所有节点即为它的左子树，右侧所有节点均为它的右子树，那么就可以进行递归左右子树了，当节点数为1时递归终止返回1。这时候小伙伴们有没有发现什么神奇的事情？？？？？？这个递增序列不就是BST的中序遍历结果吗！！！这个问题不就等同于给你一颗二叉树的中序遍历序列，让你求能构造出来多少棵二叉树吗？这时候，不知道细心的小伙伴们有没有发现，我们这个递增序列的节点值好像没有什么用啊？实际上确实如此，在没有相同节点值的情况下，我们只需要知道一个BST节点的数量就可以算出能够构造出的BST数量了（这个好像是有公式可以直接计算的，煮啵在某道数据结构考研辅导书上感觉看到过，记不大清了）。为什么这样嘞？给你一堆节点值，肯定是可以排成一个递增序列的，我们只需要知道比它大的数有多少，比它小的有多少就可以了，因为你每次递归都是将这个序列分成左右子树两部分，传递的只是每个部分的节点数量，而前面提到过递归的终止条件是节点数量为1，根本不需要关注节点的具体数值。以某个节点为根节点所能构造的BST数量即为左右子树数量之积，如果左子树或右子树为空那么数量为1。这个就是这个问题的核心算法，递归算法和动态规划算法的本质也在于此，从上述分析我们此时应该已经有了一个清晰的认知：BST的数量仅仅与节点数有关系，和节点值无关。那么我们在计算BST数量时，就可以按照节点数从小到大去计算BST的数量，计算给定节点数的BST数量时候，既可以直接调用之前已经计算过的，这就是动态规划算法，而递归算法时间复杂度较高的原因就在于它会进行多次重复性计算给定节点数的BST数量。这也是一些同一个问题可以用递归和动态规划同时解决，但时间复杂度相差较大的原因。这里给出动态规划的递推公式。

dp[i] ;//i个节点的BST数量
dp[0] = dp [1] = 1 ; //初始化
//当然了，n个节点就要进行下面计算n次，因为可以选取n个节点作为根节点
dp[n] += dp[h] * dp[k];//这里h,k即为n个节点选定某个节点为根节点时，左右子树的节点数量

基本思路就是这样，下面给出详细代码（实现方式不统一，本质思路相同）

递归算法代码

class Solution {
public:
    // 计算从节点值为left到节点值为right的范围内，可以组成的二叉搜索树的数量
    int GetExactNodeNum(int left, int right) {
        // 如果left等于right，说明只有一个节点，只有一种树的结构（单个节点本身）
        if (left == right) return 1;

        // 初始化当前范围内的树的数量为0
        int num = 0;

        // 遍历当前范围内的所有节点值，尝试将每个节点值作为根节点
        for (int i = left; i <= right; i++) {
            // 如果当前节点值i是范围内的最小值（即left），则没有左子树
            // 只需要计算右子树的数量（从i+1到right）
            if (i == left) num += GetExactNodeNum(i + 1, right);
            // 如果当前节点值i是范围内的最大值（即right），则没有右子树
            // 只需要计算左子树的数量（从left到i-1）
            else if (i == right) num += GetExactNodeNum(left, i - 1);
            // 如果当前节点值i既不是最小值也不是最大值，则既有左子树也有右子树
            // 左子树的数量为从left到i-1的树的数量
            // 右子树的数量为从i+1到right的树的数量
            // 以i为根节点的树的数量为左子树数量乘以右子树数量
            else {
                num += GetExactNodeNum(left, i - 1) * GetExactNodeNum(i + 1, right);
            }
        }

        // 返回当前范围内可以组成的二叉搜索树的数量
        return num;
    }

    // 计算由n个节点组成的二叉搜索树的数量
    int numTrees(int n) {
        // 调用GetExactNodeNum函数，从值为1的节点到值为n的节点
        return GetExactNodeNum(1, n);
    }
};

动态规划代码

class Solution {
public:
    // 动态规划函数，用于计算ans[n]的值
    void SetNumTrees(vector<int>& ans, int n) {
        int left = 0;         // 左边界，表示左子树的节点数
        int right = n - 1;    // 右边界，表示右子树的节点数
        int num = 0;          // 用于存储当前n个节点的BST数量

        // 遍历所有可能的左子树和右子树的组合
        while (left <= right) {
            // 如果左子树和右子树的节点数相同（即对称情况）
            if (left == right) {
                num += ans[left] * ans[right];  // 只有一种组合方式
            } else {
                // 如果左子树和右子树的节点数不同
                num += ans[left] * ans[right] * 2;  // 左右子树可以互换，因此乘以2
            }
            left++;  // 左子树节点数增加
            right--; // 右子树节点数减少
        }

        // 将计算结果存储到ans数组中
        ans[n] = num;
    }

    // 主函数，计算由n个节点组成的BST的数量
    int numTrees(int n) {
        vector<int> ans;       // 动态规划数组，存储每个节点数对应的BST数量
        ans.resize(n + 1);     // 初始化数组大小为n+1
        ans[0] = 1;            // 0个节点的BST数量为1（空树）
        ans[1] = 1;            // 1个节点的BST数量为1（单个节点）

        // 从2个节点开始，逐步计算到n个节点的BST数量
        for (int i = 2; i <= n; i++) {
            SetNumTrees(ans, i);  // 调用SetNumTrees函数计算ans[i]
        }

        // 返回最终结果，即n个节点的BST数量
        return ans[n];
    }
};

我这里n个节点的遍历为了降低计算量使用了优化写法，可以直接遍历的影响不大。这里的优化是：比方有个5个节点的BST，那么我分别选取第二个，第四个节点作为根节点，那么这两个情况的左右子树数量分别为（1，3）（3，1），很明显根据我们之前的分析，这两种情况构造出来的数量相等，直接乘以2。 

煮啵是个新手，写的很口语化，感谢观看！！！