模式分解这边主要包括无损分解和保持函数依赖的分解两种形式,简单整理一下。
无损分解
把一个 RRR 分成 ρ={R1,R2,⋯ ,Rk}\rho =\{R_1,R_2,\cdots,R_k\}ρ={R1,R2,⋯,Rk},然后通过自然连接 R1⋈R2⋈⋯⋈RkR_1\bowtie R_2\bowtie \cdots\bowtie R_kR1⋈R2⋈⋯⋈Rk,如果连回来了就是无损分解,如果多出了一些冗余元组就是有损分解。
这个定义很难直接用来判定,下面介绍一个判定算法。
判定算法
术语描述
ρ={R1<U1,F1>,⋯ ,Rk<Uk,Fk>}\rho = \{R_1<U_1,F_1>,\cdots,R_k<U_k,F_k>\}ρ={R1<U1,F1>,⋯,Rk<Uk,Fk>} 是 R<U,F>R<U,F>R<U,F> 的一个分解,U={A1,⋯ ,An}U=\{A_1,\cdots,A_n\}U={A1,⋯,An},F={FD1,⋯ ,FDρ}F=\{\mathrm{FD_1,\cdots,FD}_\rho\}F={FD1,⋯,FDρ}(必须是极小依赖集),其中 FDi:=Xi→Ali\mathrm{FD}_i:=X_i\rightarrow A_{li}FDi:=Xi→Ali。算法的过程:
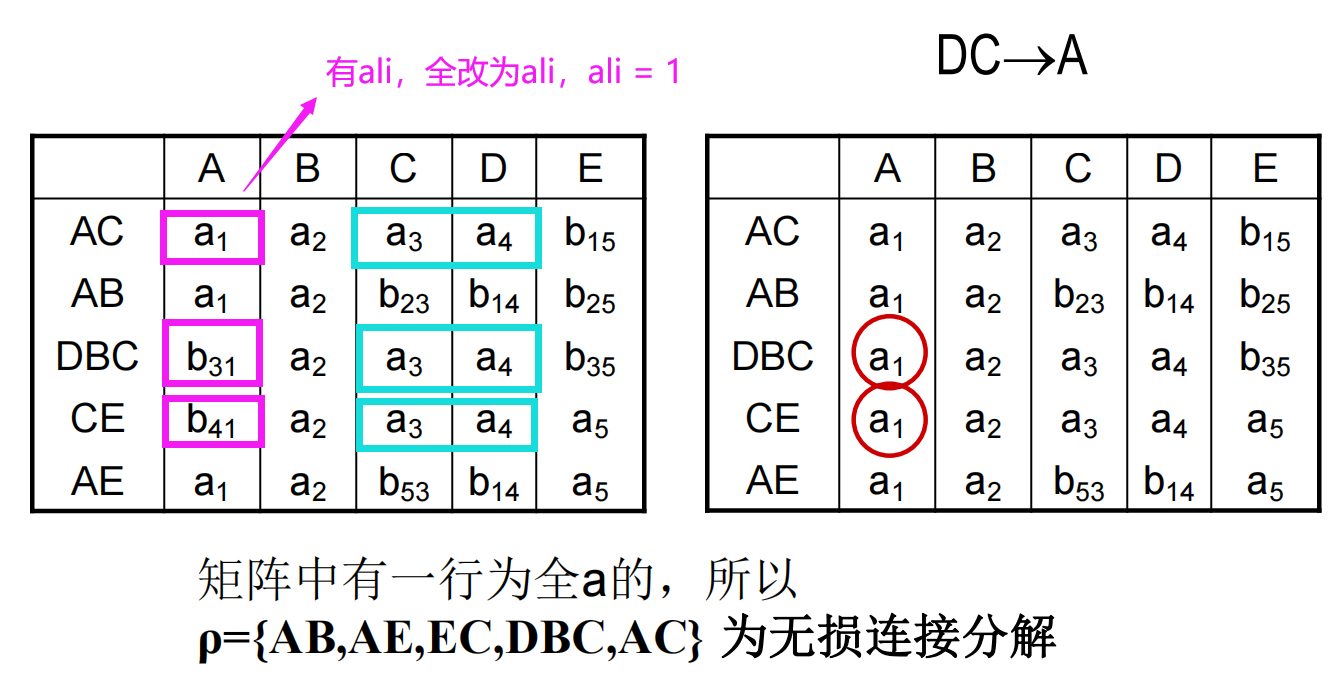
(1)(1)(1) 建立 k×nk\times nk×n 表 C=[cij]k×n\boldsymbol C=[c_{ij}]_{k\times n}C=[cij]k×n,每列对应属性 Aj(j=1,⋯ ,n)A_j(j=1,\cdots,n)Aj(j=1,⋯,n),每行对应一个分解的 UiU_iUi。cij={aj,Aj∈Ui,bij,Aj∉Uic_{ij}=\displaystyle\begin{cases}a_j,&A_j\in U_i,\\b_{ij},&A_j\notin U_i\end{cases}cij={aj,bij,Aj∈Ui,Aj∈/Ui。
(2)(2)(2) 遍历 FDi\mathrm{FD}_iFDi,截取 C\boldsymbol CC 中对应 XiX_iXi 的列,看看哪些行的内容是相同的。这些行在 lilili 列若存在一个 alia_{li}ali,那么这些行在 lilili 列的值全部改为 alia_{li}ali;否则全部改为 bmlib_{mli}bmli,其中 mmm 为这些行的行号最小值。
一个符号被更改,表中其它所有相同的符号都应作相同的更改。
(3)(3)(3) 重复 (2)(2)(2) 的操作,如果有一行全 aaa 说明 ρ\rhoρ 是无损连接分解,停止算法;否则表 C\boldsymbol CC 总会在某个时刻不再更新,停止算法并下结论 ρ\rhoρ 是有损连接分解。
案例描述(直接上图)
设有关系模式 R(A,B,C,D,E)R(A,B,C,D,E)R(A,B,C,D,E),RRR 的最小函数依赖集是 F={A→D,E→D,D→B,BC→D,DC→A}\mathit{F=\{A→D,E →D,D →B,BC →D,DC →A}\}F={A→D,E→D,D→B,BC→D,DC→A}。判断 ρ={AB,AE,EC,DBC,AC }\mathit{ρ=\{AB,AE,EC,DBC,AC\ \}}ρ={AB,AE,EC,DBC,AC } 是否为无损连接分解。
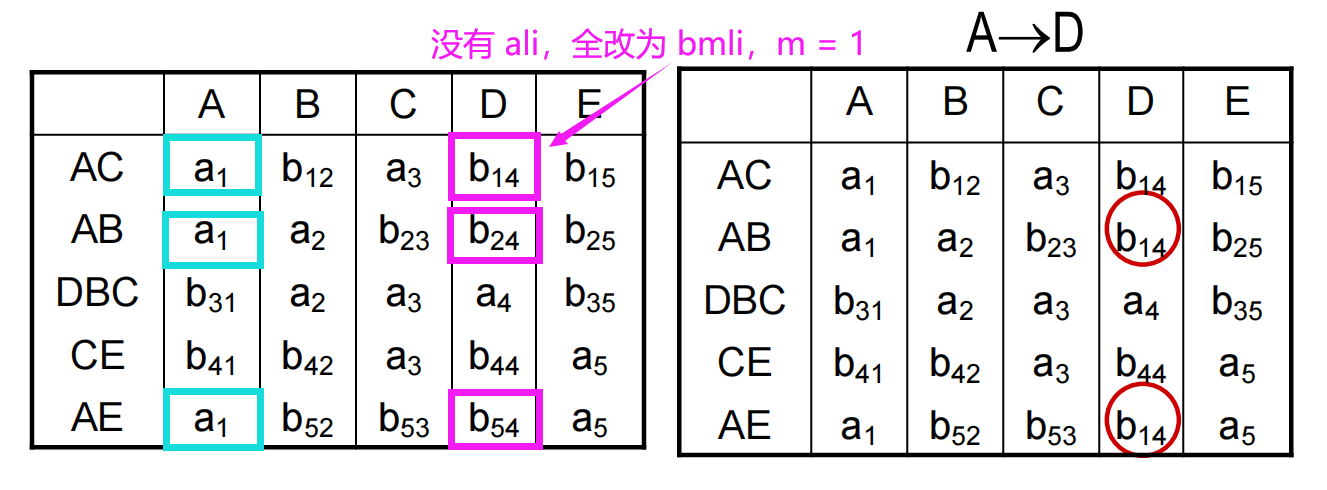
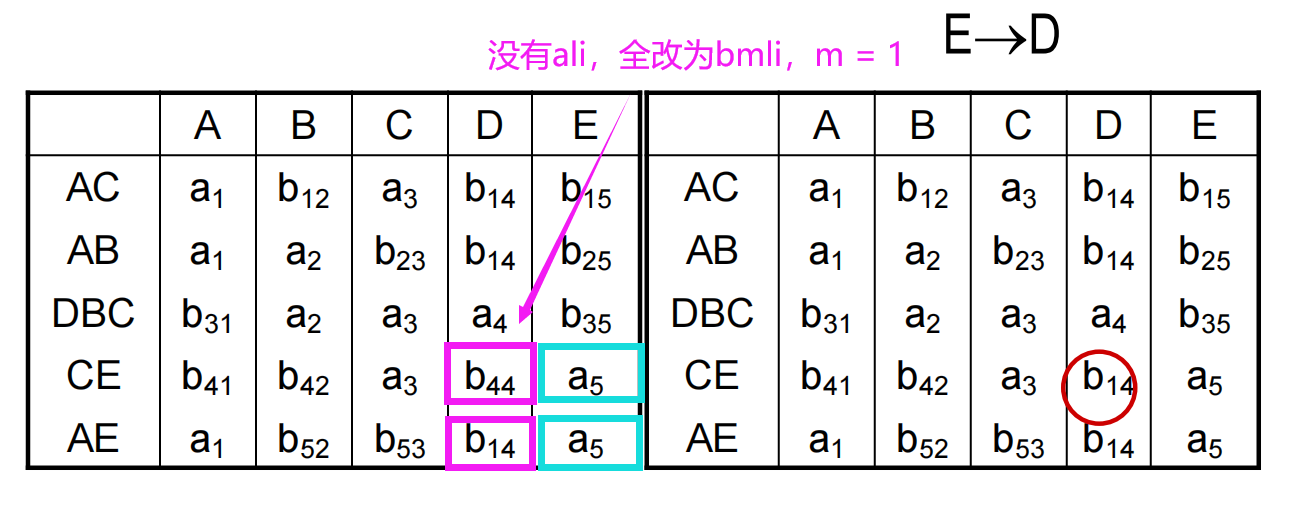
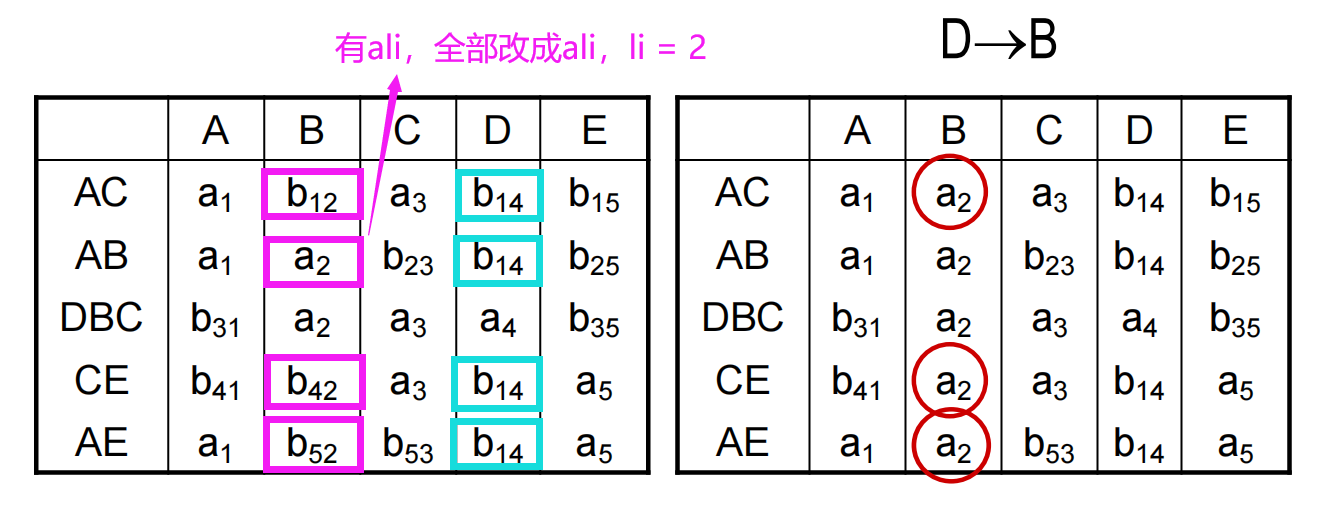
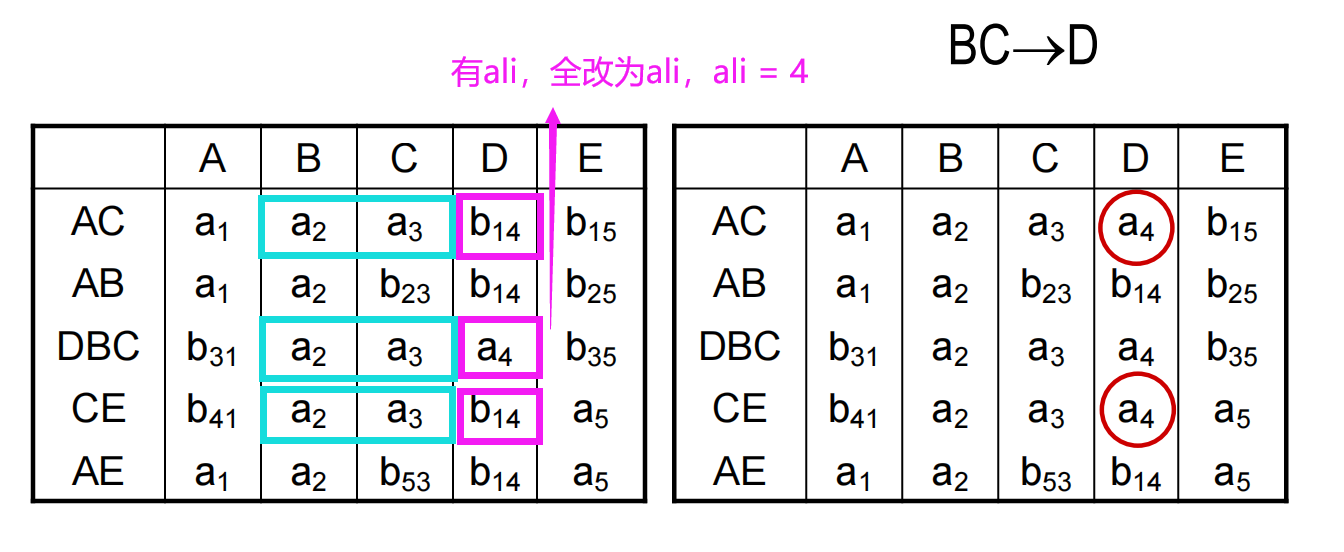
判定定理(分解为 2 个关系)
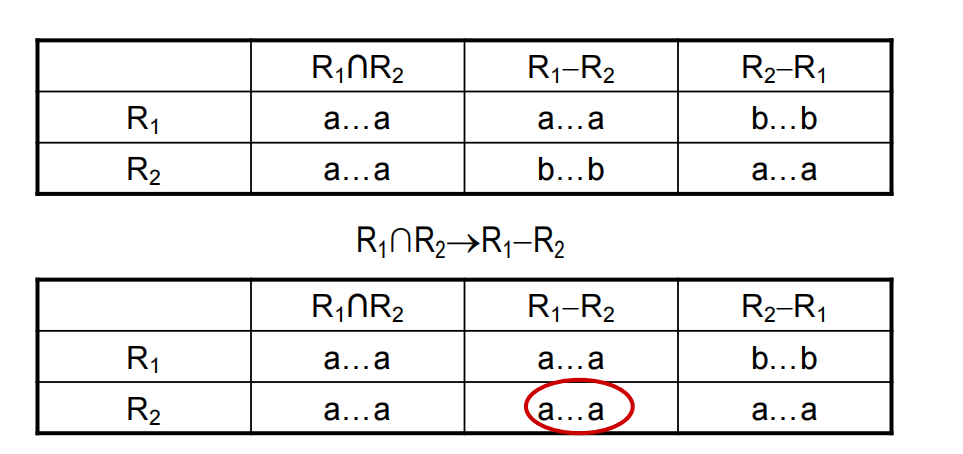
定理描述:对于 R<U,F>R<U,F>R<U,F> 的一个分解 ρ={R1<U1,F1>,R2<U2,F2>}\rho = \{R_1<U_1,F_1>,R_2<U_2,F_2>\}ρ={R1<U1,F1>,R2<U2,F2>},如果 U1∩U2→U1−U2∈F+U_1\cap U_2\rightarrow U_1-U_2\in F^+U1∩U2→U1−U2∈F+ 或 U1∩U2→U2−U1∈F+U_1\cap U_2\rightarrow U_2-U_1\in F^+U1∩U2→U2−U1∈F+,则 ρ\rhoρ 具有无损连接性。
这个定理可以从上面的算法得出,具体证明看下图就知道了。
保持函数依赖的分解
把一个 RRR 分成 ρ={R1,R2,⋯ ,Rk}\rho =\{R_1,R_2,\cdots,R_k\}ρ={R1,R2,⋯,Rk},然后看看是否有 F1+∪F2+∪⋯∪Fk+=F+F_1^+\cup F_2^+\cup\cdots\cup F_k^+=F^+F1+∪F2+∪⋯∪Fk+=F+,如果相等就是保持函数依赖的分解,否则不是。
这个定义可以直接用来判定。
模式分解算法
保持函数依赖的 3NF 分解
描述
(1)(1)(1) 对 R<U,F>R<U,F>R<U,F>中的 FFF进行极小化处理。处理后的函数依赖集仍用 FFF 表示。
(2)(2)(2) 找出不在 FFF 中出现的属性,把这样的属性构成一个关系模式,并把这些属性从 UUU 中去掉。
(3)(3)(3) 如果 FFF 中有一个函数依赖涉及 RRR 的全部属性,则 RRR 不能再分解。
(4)(4)(4) 如果F中含有 X→AX→AX→A,则分解应包含模式 XAXAXA,如果 X→A1,X→A2,⋯ ,X→AnX→A_1,X→A_2,\cdots,X→A_nX→A1,X→A2,⋯,X→An 均属于 FFF,则分解应包含模式 XA1A2⋯An\mathit{XA}_1A_2\cdots A_nXA1A2⋯An。
例子
设关系模式 R<U,F>R<U,F>R<U,F>,U={C,T,H,R,S,G,X,Y,Z}U=\{C,T,H,R,S,G,X,Y,
Z\}U={C,T,H,R,S,G,X,Y,Z},F={C→T,CS→G,HR→C,HS→R,TH→R,C→X}F=\mathit{\{C→T,CS→G,HR→C,HS→R,TH→R,C→X\}}F={C→T,CS→G,HR→C,HS→R,TH→R,C→X},将 RRR 分解为 3NF\rm3NF3NF,且保持函数依赖。
解:设该函数依赖集已经是最小化的,先对 FFF 中左边相同的进行合并 (C→T+C→X=C→TX)(C→T +C→X=C\rightarrow\mathit{TX})(C→T+C→X=C→TX) 得 F={C→TX,CS→G,HR→C,HS→R,TH→R}F=\mathit{\{C→TX,CS→G,HR→C,HS→R,TH→R\}}F={C→TX,CS→G,HR→C,HS→R,TH→R}。
因此 ρ={YZ,CTX,CSG,HRC,HSR,THR}\mathit{\rho=\{YZ,CTX,CSG,HRC,HSR,THR\}}ρ={YZ,CTX,CSG,HRC,HSR,THR}。
YZ\mathit{YZ}YZ 是 FFF 中没有出现的属性,单独拿出来。
保持函数依赖的无损 3NF 分解
在保持函数依赖的 3NF 分解基础上,尝试在 ρ\rhoρ 中加入 RRR 的码(一个就够了)得 τ\tauτ。加入后可能会存在包含关系,保大去小。举个例子说明。
有关系模式R<U,F>R<U,F>R<U,F>,U={C,T,H,R,S,G}U=\{C,T,H,R,S,G\}U={C,T,H,R,S,G},F={C→T,CS→G,HR→C,HS→R,TH→R}\mathit{F=\{C→T,CS→G,
HR→C,HS→R,TH→R\}}F={C→T,CS→G,HR→C,HS→R,TH→R},将 RRR 分解为 3NF\rm3NF3NF,且既具有无损连接性又能保持函数依赖。
解:求得关系模式 RRR 的码为 HS\mathit{HS}HS,它的一个保持函数依赖的 3NF\rm3NF3NF为:ρ={CT,CSG,HRC,HSR,THR}\mathit{\rho=\{CT,CSG,HRC,HSR,THR\}}ρ={CT,CSG,HRC,HSR,THR}。
因为码 HS⊂HSR\mathit{HS\subset HSR}HS⊂HSR,所以去掉 HS\mathit{HS}HS,保留 HSR\mathit{HSR}HSR。所以 τ=ρ={CT,CSG,HRC,HSR,THR}\mathit{\tau=\rho=\{CT,CSG,HRC,HSR,THR\}}τ=ρ={CT,CSG,HRC,HSR,THR}为满足要求的分解。
该例题是唯一候选码,当有多个候选码的时候,选一个加入 ρ\rhoρ 使得 ρ=τ\rho=\tauρ=τ。如果找不到这样的候选码,随便加一个进去就行。
























 1170
1170

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








