第二十五章 数论——约数

一、什么是约数

如果a%b==0，那么b就叫做a的约数，a和b必须是整数。

二、约数的求解——试除法

1、问题

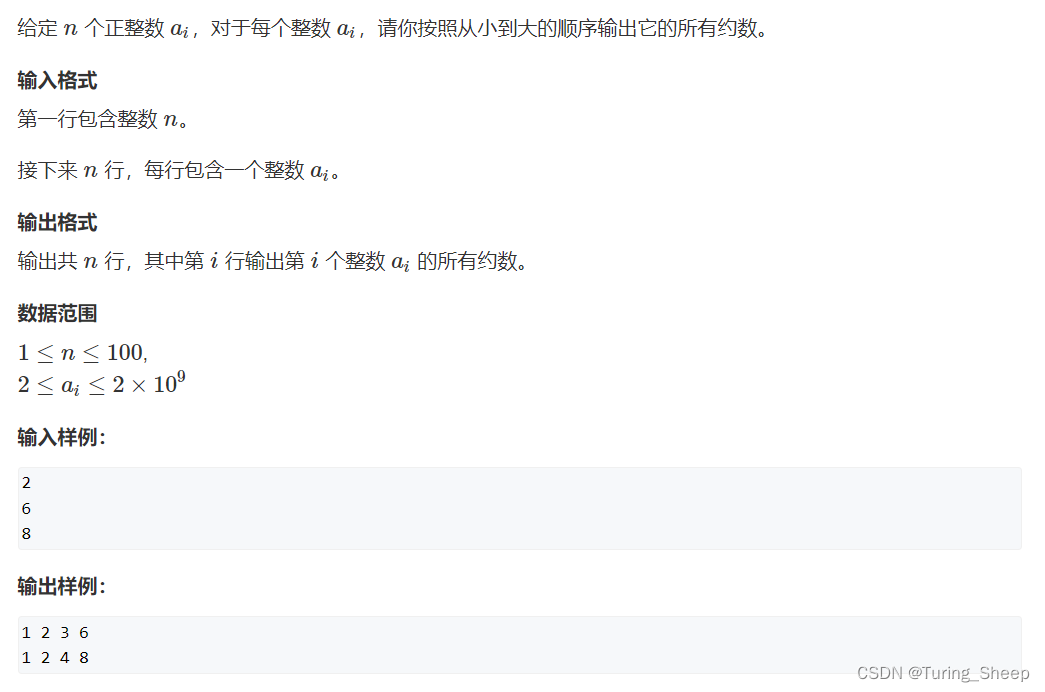
2、思路分析

我们只需要枚举1到n的所有数字即可，看看这个范围内的数字是否满足$a$ % $b==0$。这个过程的复杂度是$O(n)$。

那么我们如何优化呢？

约数必定是成对出现的，所以我们只需要算出一个，那么另外一个就可以利用公式：$a/b$计算出来。也就是说我们只需要找到一半的约数。

而这一半的约数必定是在$1$到$\sqrt{n}$的。

我们可以简单的证明一下，假设n存在一对约数，这对约数中的两个值都大于$\sqrt{n}$，那么此时二者的乘积必定大于$n$，并不等于n，所以此时这两个数不是n的约数，故假设不成立。所以我们提出的结论是对的。

但是我们还需要避免重复输出的情况：

比如数字$9$

$9=3\ast 3$，这两个约数其实是一个，所以需要特判一下，

3、代码实现

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int n;
void f(int a)
{
    vector<int>v;
    for(int i=1;i<=a/i;i++)
    {
        if(a%i==0)
        {
            v.push_back(i);
            if(i!=a/i)
                v.push_back(a/i);
        }
    }
    sort(v.begin(),v.end());
    for(int i=0;i<v.size();i++)
    {
        cout<<v[i]<<" ";
    }
    puts("");
}
int main()
{
    cin>>n;
    while(n--)
    {
        int a;
        cin>>a;
        f(a);
    }
}

三、约数个数

1、问题描述

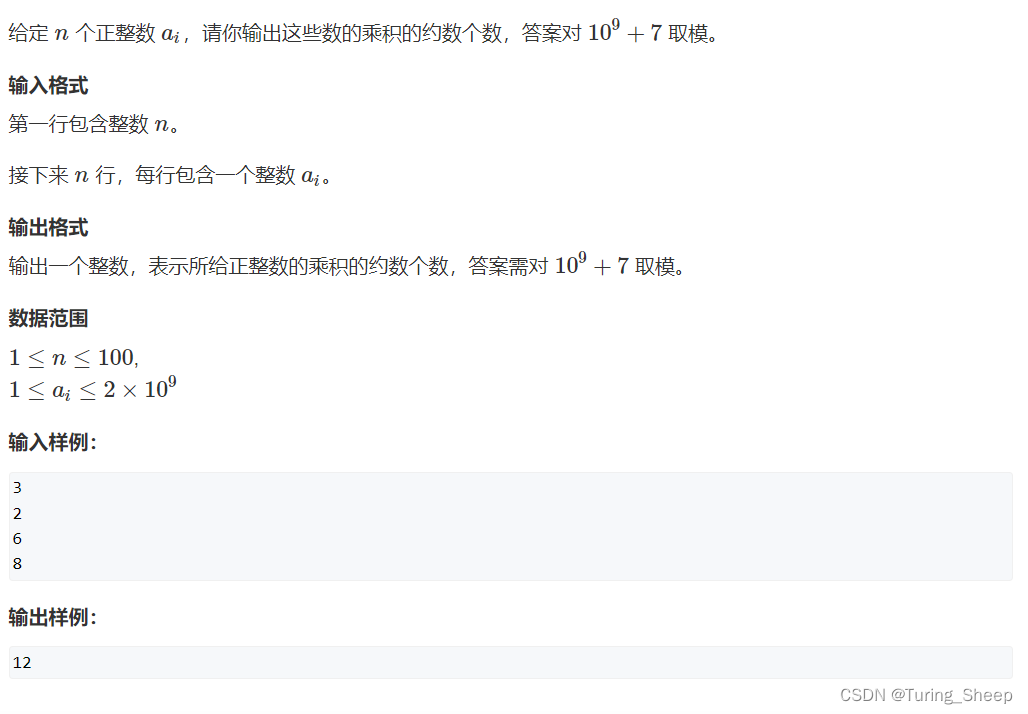
2、算法思路

根据算数基本定理：
我们任何一个合数都可以写成有限个质数的乘积：
$$n=p_1^q\ast p_2^w\ast p_3^e...p_n^m$$

上面的式子中，我们任意取出几个$p$，就能组成$n$的约数。

因此这就是一个排列组合的问题。

对于$p_1$而言，我们可以取出$[0,q]$个，共$q+1$种取法。

后面的也同理，那么根据乘法原理：

我们的约数的个数为：

$$(q+1)\ast (w+1)\ast (e+1)...(m+1)$$

所以我们的目的就是求出一个数的所有质因数的指数，对于如何求解一个数的质因数，请看前面关于质数的文章。

质因数文章的传送门

由于质因数和指数的是紧密相关的。因此，我们可以利用质因数去索引指数，为了提高索引的效率，我们可以使用哈希表。

3、代码实现

#include<iostream>
#include<unordered_map>
const int mod=1e9+7;
using namespace std;
unordered_map<int,int>primes;
int n,a;
void f(int a)
{
	//求解质因数
    for(int i=2;i<=a/i;i++)
    {
        if(a%i==0)
        {
            while(a%i==0)
            {
            	//记录质因数的指数
                primes[i]++;
                a/=i;
            }
        }
    }
    if(a>1)primes[a]++;
}

int main()
{
    cin>>n;
    while(n--)
    {
        cin>>a;
        f(a);
    }
    long long res = 1;
    //利用公式计算个数
    for (auto p : primes)
        res = res * (p.second + 1) % mod;
    cout<<res<<endl;
    return 0;
}

四、约数之和

1、问题描述

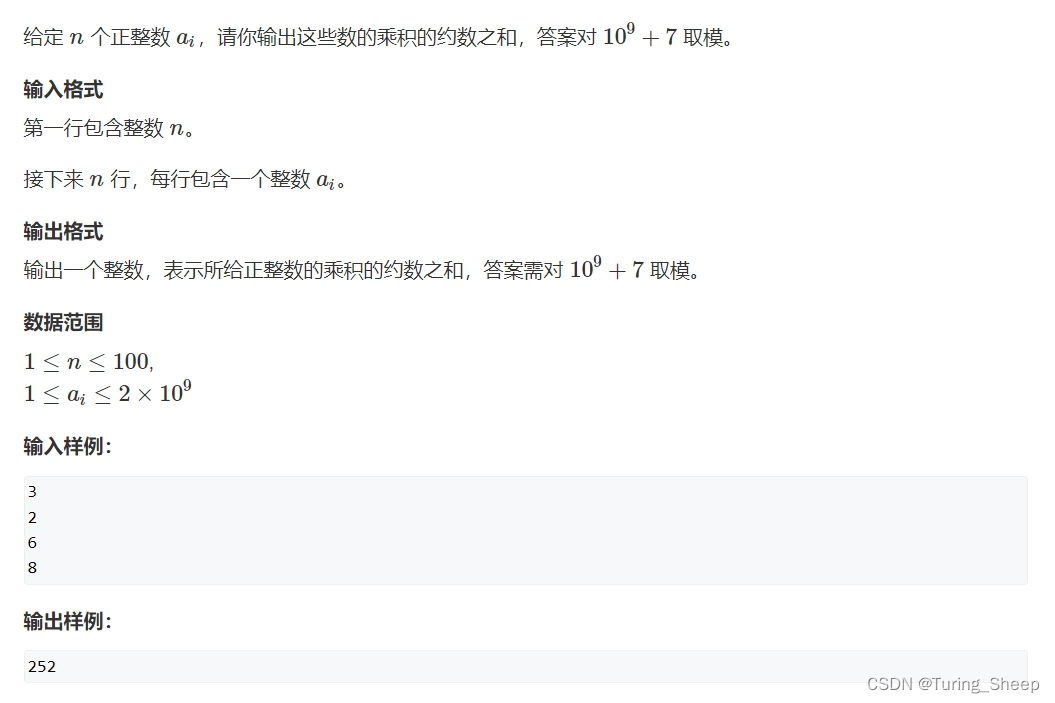
2、算法思路

我们同样采取算术基本定理的方式去求解：

$$n=p_1^q\ast p_2^w\ast p_3^e...p_n^m$$

而我们将约数之和记作：$sum$

那么

$$sum=$$
$$(p_1^0+p_1^1+p_1^2...p_1^q)\ast (p_2^0+p_2^1+p_2^2...p_2^w)\ast (p_3^0+p_3^1+p_3^2...p_3^e)...(p_n^0+p_n^1+p_n^2...p_n^m)$$

想要证明上述的公式其实很简单，直接将上面的多项式展开就行了。作者这里就不展开了。

那么这道题的思路就很明确了，依旧是求一个数的质因数以及对应的指数。然后按照上面的公式求解。

此时我们需要再介绍一个算法，秦九韶算法

对于式子：
$$p_1^0+p_1^1+p_1^2...p_1^q$$
我们令
$t=1$
然后接下来循环$q$次
$t=t\ast p_1+1$

第一次循环：$t=1+p_1^1$

第二次循环$t=t\ast p1+1=1+p_1^1+p_1^2$

第三次循环$t=1+p_1^1+p_1^2+p_1^3$

…

第q次循环：$t=1+p_1^1+p_1^2...p_1^q$

3、代码实现

#include<iostream>
#include<unordered_map>
using namespace std;
const int mod=1e9+7;
int n,a;
unordered_map<int,int>primes;
int main()
{
    cin>>n;
    while(n--)
    {
        cin>>a;
        for(int i=2;i<=a/i;i++)
        {
            while(a%i==0)
            {
                primes[i]++;
                a/=i;
            }
        }
        if(a>1)primes[a]++;
    }
    long long sum=1;
    for(auto x:primes)
    {
        long long t=1;
        int p=x.first,e=x.second;
        while(e--)t=(t*p+1)%mod;
        sum=sum*t%mod;
    }
    cout<<sum<<endl;

}

五、最大公约数——欧几里德算法

1、问题描述

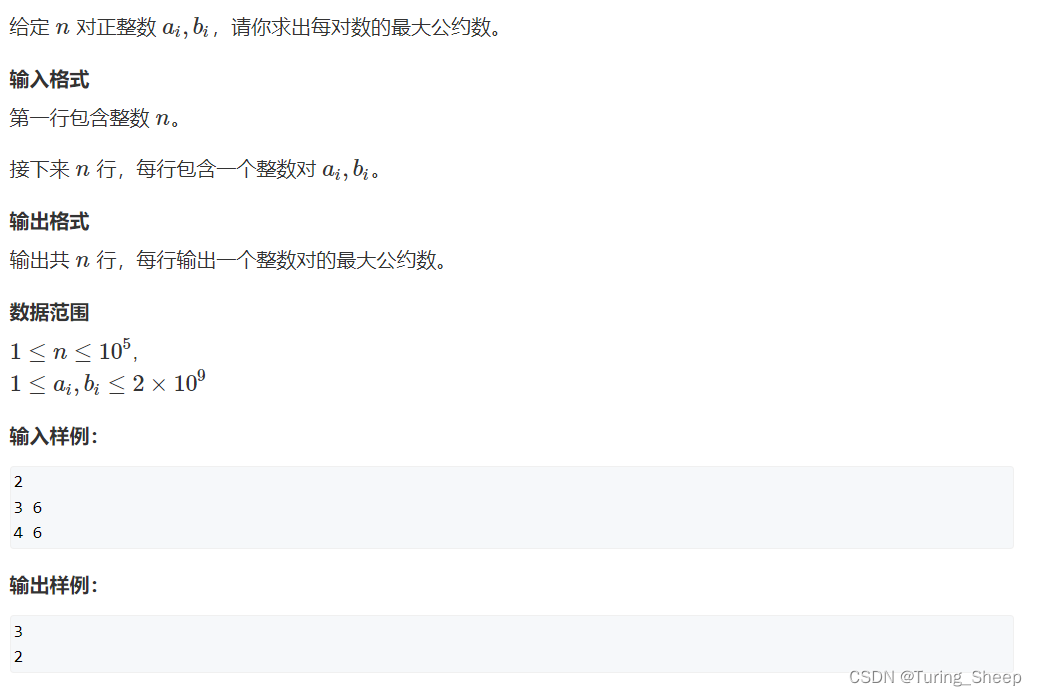
2、算法思路

（1）算法内容

$a$和$b$的最大公约数等于$a$与$a$ $mod$ $b$的最大公约数。
表达式为：

$$gcd(a,b)=gcd(b,amodb)$$

（2）算法证明

我们先明确这样一个表示方法：

如果$amodb=0$，就说明$b$能够整除$a$，记作$b|a$

$$若d|a，d|b，则d|(ka+mb)$$

---

证明：
令 $a/d=x_1$，$b/d=x_2$

那么

$$(ka+mb)/d=(k{x}_{1}d+m{x}_{2}d)/d=k{x}_1+m{x}_2$$

因为$k{x}_1+m{x}_2$ 是整数，所以结论成立。

---

接着:

$amodb=a-[a/b]\ast b$，其中$f(x)=[x]$为取整函数（高斯函数）。

那么这个式子可以简写为：
$$amodb==a-c\ast b$$
所以
$$gcd(b,amodb)=gcd(b,a-c\ast b)$$

现在假设：

$$d|a,d|b$$

所以
$$d|(a-c\ast b)$$
即：
$$d|(amodb)$$

其中，因为：$d|a,d|b$，所以$d$是$a$和$b$的公约数。

又因为$d|b,d|(amodb)$，所以$d$是$b$和$(amodb)$的公约数。

所以，二者最大公约数相同。

即：
$$gcd(a,b)=gcd(b,amodb)$$

3、代码实现

#include<iostream>
using namespace std;
int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<gcd(a,b)<<endl;
    }
}