自动机 DFA/NFA | 定义、对比、转换、实例及应用

注：本文为 “自动机 DFA/NFA” 相关合辑。
英文引文，机翻未校。
如有内容异常，请看原文。

---

DFA : definition, representations, application ( Deterministic Finite Automata )

确定性有限自动机（DFA）：定义、表示方法及应用

By Er Parag Verma
Feb 23, 2016

Deterministic Finite Automata:

确定性有限自动机

The first type of finite automata is named Deterministic Finite Automata (DFA). DFA have a rich background in terms of the mathematical theory underlying their development and use. Informally DFA is defined as, “Deterministic finite automaton is a simple idealized machine used to recognize pattern within input takes from some set of symbols or alphabet $\sum$”. The main job of DFA is to accept or reject an input depending on whether the pattern defined by the finite automata occurs in the input. DFA is also called deterministic finite state machine or deterministic finite accepter.
有限自动机的第一类为确定性有限自动机（DFA）。确定性有限自动机的设计与应用依托深厚的数学理论基础。其非形式化定义为：“确定性有限自动机是一种理想化的简单机器，用于识别取自某一符号集合（即字母表 $\sum$）的输入字符串中的模式”。确定性有限自动机的核心功能是根据输入字符串中是否存在该自动机定义的模式，决定接受或拒绝该输入。确定性有限自动机也被称为确定性有限状态机或确定性有限接受器。

Analytically a deterministic finite automaton is defined by five-tuples are as follows;
从解析角度而言，确定性有限自动机可由五元组定义，形式如下：
$M=(Q,\Sigma ,\delta ,q_0,F)$
Where, each tuple have its specification and own definition.
式中，五元组的每一个元素均有其特定含义与定义。

1. Q: It represents the finite non-empty set states. All the finite number of states which is the part of M participates in Q.
   $Q$：表示非空有限状态集合。构成自动机 $M$ 的全部有限个状态均包含于集合 $Q$ 中。

2. Σ: It presents the non-empty finite set of the input alphabet.
   $\Sigma$：表示非空有限输入字母表集合。

3. δ : It represents the state transition function which maps $Q\times \Sigma \to Q$. It is usually called direct transition function. The state transition function takes the current state from Q and an input alphabet from $\Sigma$ and returns the new set of output alphabets and the next state. This function mapping is usually represented by a transition table or a transition diagram.
   $\delta$：表示状态转移函数，映射关系为 $Q\times \Sigma \to Q$，该函数也常被称为直接转移函数。状态转移函数以 $Q$ 中的当前状态与 $\Sigma$ 中的输入符号为参数，输出对应的下一状态（原文“输出字母表集合”表述有误，状态转移函数的输出为下一状态）。该函数映射关系通常可由转移表或转移图表示。

4. q0: It is the initial state (which may be fixed or variable depends on machine behavior). $q_0\in Q$
   $q_0$：表示初始状态，其是否固定取决于自动机的运行机制，满足 $q_0\in Q$。

5. F: It is the set of final states ($F\subseteq Q$). It is assumed here that there may be more than one final state.
   $F$：表示终止状态集合，满足 $F\subseteq Q$。本定义中允许存在多个终止状态。

Representation of DFA:

确定性有限自动机的表示方法

A DFA can be represented by the following ways;
确定性有限自动机可通过以下三种方式表示：

1. Transaction diagram DFA or State diagram
   转移图（又称状态图）

2. Transaction table DFA
   转移表

3. Language of DFA
   确定性有限自动机对应的语言

Transaction diagram DFA:

确定性有限自动机的转移图

Transaction diagram is the graphical representation of a DAF. It is also called state transaction diagram. To represent the behavior of a machine under DFA we are using digraph where;
转移图是确定性有限自动机的图形化表示形式，也被称为状态转移图。转移图采用有向图描述确定性有限自动机的运行行为，各元素定义如下：

• Nodes or vertices of the digraph represent the states that belong to set of states Q, and
  有向图的节点（顶点）对应状态集合 $Q$ 中的元素。

• The connected arcs or arrow labeled with an input alphabets from $\sum$ that show the transition.
  有向图的有向边（箭头）由输入字母表 $\sum$ 中的符号标记，代表状态转移关系。

• The initial state is denoted by a circle with an empty single incoming arc.
  初始状态的表示方式为：一个圆形节点，外部有一条无起点的有向边指向该节点。

• The finial state is indicated by double circles.
  终止状态采用双层圆形节点表示。

Transaction table:

转移表

A transaction table is a tabular representation that used to represents the working behavior of transaction function $\delta$ that takes two arguments as input and returns a output state. Transaction table represents all the moves of a finite semi automaton or finite state machine based on the current state and other inputs. Formally a transaction table is a 2-dimension array which consist rows and columns where;
转移表是状态转移函数 $\delta$ 运行行为的表格化表示形式，该函数以当前状态与输入符号为两个参数，输出对应的下一状态。转移表可完整描述有限半自动机或有限状态机基于当前状态与输入符号的全部转移过程。形式上，转移表是一个二维数组，包含行与列两个维度，各维度定义如下：

• The columns contain the state in which the machine will be on the input alphabets $\sum$ represented by that column.
  列维度由输入字母表 $\sum$ 中的符号构成，每一列对应一个输入符号。

• The rows corresponds to the state of the finite control unit can be in or it contains the states of finite automata machine (current state and/or next state).
  行维度对应有限控制器的状态，包含该有限自动机的全部状态（当前状态与下一状态）。

• The entry for one row corresponding to state $q_i$ and the column corresponds to input a is the state $\delta (q_i,a)$.
  行对应状态 $q_i$ 且列对应输入符号 $a$ 时，表格对应位置的元素为状态 $\delta (q_i,a)$。

A transaction table is essentially a truth table in which some of the inputs are the current state, and the outputs include the next state, along with other outputs. A transaction table is also called state transaction diagram.
转移表本质上是一种真值表，其输入包含当前状态，输出包含下一状态及其他相关输出。转移表也可被称为状态转移表（原文“状态转移图”表述有误，此处应为表格形式）。

Language:

确定性有限自动机对应的语言

The language of DFA consist a set of all strings chosen from ${\sum }^{\ast }$ that all are accepted by machine M.
确定性有限自动机对应的语言，是由字母表闭包 ${\sum }^{\ast }$ 中所有能被自动机 $M$ 接受的字符串构成的集合。

Example of DFA:

确定性有限自动机实例

Represent the DFA of machine
构造如下确定性有限自动机
M = ( { q 0 , q 1 , q 2 } , { 0 , 1 } , δ , q 0 , { q 1 } ) M = (\{q_0, q_1, q_2\}, \{0, 1\}, \delta, q_0, \{q_1\}) M=({q0​,q1​,q2​},{0,1},δ,q0​,{q1​}), where $\delta$ is given as;
M = ( { q 0 , q 1 , q 2 } , { 0 , 1 } , δ , q 0 , { q 1 } ) M = (\{q_0, q_1, q_2\}, \{0, 1\}, \delta, q_0, \{q_1\}) M=({q0​,q1​,q2​},{0,1},δ,q0​,{q1​})，其中转移函数 $\delta$ 的定义如下：

$$\begin{gathered} \delta (q_0,1)=q_0 \\ \delta (q_0,0)=q_2 \\ \delta (q_2,0)=q_2 \\ \delta (q_2,1)=q_1 \\ \delta (q_1,0)=q_1 \\ \delta (q_2,0)=q_1 \end{gathered}$$

State transaction diagram of machine ‘M’:

自动机 $M$ 的状态转移图

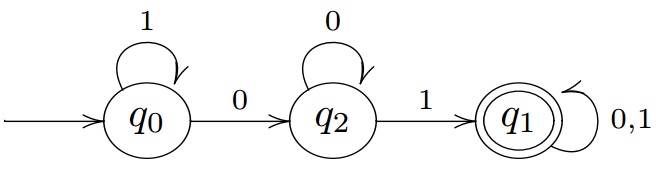
State transaction graph DFA
确定性有限自动机状态转移图

State transaction table of machine ‘M’:

自动机 $M$ 的状态转移表

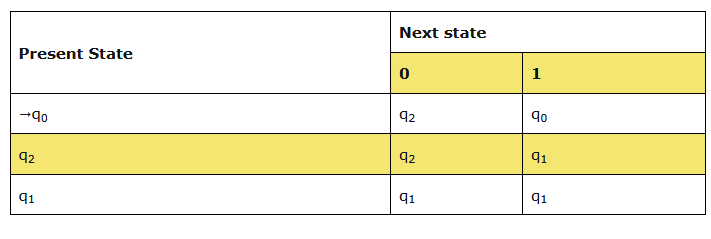
Language of DFA of machine ‘M’:

自动机 $M$ 对应的语言

L M = { 1 ∗ 0 0 ∗ 1 ( 0 , 1 ) ∗ } L_M = \{1^*00^*1(0, 1)^*\} LM​={1∗00∗1(0,1)∗} or
L M = { 1 ∗ 0 0 ∗ 1 ( 0 + 1 ) ∗ } L_M = \{1^*00^*1(0+1)^*\} LM​={1∗00∗1(0+1)∗} or
L M = { 1 ∗ 0 0 ∗ 1 0 ∗ 1 ∗ } L_M = \{1^*00^*10^*1^*\} LM​={1∗00∗10∗1∗}

Application of DFA ( Deterministic Finite Automata):

确定性有限自动机（DFA）的应用

As DFA have a rich background in terms of the mathematical theory underlying their development it has wide application that we are used our daily life directly or indirectly, some of them are as follows;
由于确定性有限自动机的设计依托深厚的数学理论基础，其在日常生活中有着广泛的直接或间接应用，部分应用场景如下：

• Protocol analysis
  协议分析

• Text parsing,
  文本解析

• Video game character behavior,
  视频游戏角色行为控制

• Security analysis,
  安全分析

• CPU control units,
  中央处理器控制单元

• Natural language processing
  自然语言处理

• Speech recognition, etc.
  语音识别 等

---

NFA: Nondeterministic Finite Automata Definition, Example, Application

非确定性有限自动机（NFA）：定义、实例及应用

By Er Parag Verma
Feb 23, 2016

Another type of finite automata is Non Deterministic Finite Automata (NDFAs), sometimes it is known as NFAs, does not need to obey the restrictions of finite automata as DFAs. NDFA or NFAs were introduced in 1959 by Michael O. Rabin and Dana Scott. M.O. Robin and D. Scott also showed their equivalence to DFA.
有限自动机的另一类别为非确定性有限自动机（NDFA），该模型亦常被简称为 NFA，其无需遵循确定性有限自动机（DFA）的限制条件。非确定性有限自动机由迈克尔·O·拉宾与达纳·斯科特于 1959 年提出，这两位学者同时证明了非确定性有限自动机与确定性有限自动机的等价性。

Informally an NFA is similar to a DFA i.e, “NFAs is simple machine that used to recognize the pattern with consumes a string of input symbols or alphabet $\sum$. For each input symbol, it transitions to a new state until all input symbols have been consumed and machine reaches its final state”. Unlike deterministic finite automata, it is non-deterministic finite automata, which means for some state and input symbol, the next state may be nothing or one or more than one possible next states. Thus, in the formal definition of NFA, the next states in the transaction function ‘$\delta$’ is an element of the power set of the states, which is a set of states to be considered at once. The notion of accepting an input is similar to that for the DFA. When the last input symbol from input string over alphabet $\sum$ is consumed, the NFA accepts if and only if there is some set of transitions that will take it to an accepting state. Equivalently, it rejects, if, no matter what transitions are applied, it would not end in an accepting state.
非确定性有限自动机的非形式化定义与确定性有限自动机相似，表述如下：“非确定性有限自动机是一种简易机器，其通过读取由输入符号（即字母表 $\sum$ 中的元素）构成的字符串实现模式识别。对于每一个输入符号，机器都会完成一次状态转移，直至所有输入符号读取完毕，且机器进入终止状态”。与确定性有限自动机不同，非确定性有限自动机的核心特征为非确定性，即对于某一状态与某一输入符号的组合，对应的下一状态可能为空集、单元素集合或多元素集合。因此，在非确定性有限自动机的形式化定义中，转移函数 $\delta$ 的输出为状态集合的幂集中的元素，该输出代表机器可同时处于的多个状态。非确定性有限自动机的输入接受规则与确定性有限自动机类似：当字母表 $\sum$ 上的输入字符串被完全读取后，当且仅当存在至少一条转移路径可使机器进入接受状态时，该输入字符串才会被非确定性有限自动机接受；反之，若所有可能的转移路径均无法使机器进入接受状态，则该输入字符串会被拒绝。

NFAs are used in the implementation of regular expressions: Thompson’s construction is an algorithm for compiling a regular expression to an NFA that can efficiently perform pattern matching on strings.
非确定性有限自动机可用于正则表达式的实现，典型算法为汤普森构造法。该算法能够将正则表达式编译为等价的非确定性有限自动机，进而实现高效的字符串模式匹配。

Analytically a non-deterministic finite automaton is defined by five-tuples are as follows;
从解析角度而言，非确定性有限自动机可由五元组定义，形式如下：
$M=(Q,\Sigma ,\delta ,q_0,F)$

Where, each tuple have its specification and own definition.
式中，五元组的每一个元素均有其特定含义与定义。

1. Q: It represents the finite non-empty set states. All the finite number of states which is the part of M participates in Q.
   $Q$：表示非空有限状态集合。构成自动机 $M$ 的全部有限个状态均包含于集合 $Q$ 中。

2. Σ: It presents the non-empty finite set of the input alphabet.
   $\Sigma$：表示非空有限输入字母表集合。

3. δ : It represents the state transition function which maps $Q\times \Sigma \to Q^2\to \mathcal{P}(Q)$. It is usually called direct transition function. The state transition function takes the current state from Q and an input alphabet from $\Sigma$ and returns the new set of output alphabets and the next state. This function mapping is usually represented by a transition table or a transition diagram. Here, $\mathcal{P}(Q)$ denotes the power set of Q. Let $S=x_1{x}_2\dots x_n$ be a word over the alphabet $\Sigma$. The automaton M accepts the word w if a sequence of states, $r_0,r_1,\dots ,r_n$, exists in Q with the following conditions:
   $\delta$：表示状态转移函数，映射关系为 $Q\times \Sigma \to Q^2\to \mathcal{P}(Q)$，该函数也常被称为直接转移函数。状态转移函数以 $Q$ 中的当前状态与 $\Sigma$ 中的输入符号为参数，输出对应的下一状态集合（原文“输出字母表集合”表述有误，状态转移函数的输出为下一状态集合）。该函数映射关系通常可由转移表或转移图表示。其中，$\mathcal{P}(Q)$ 表示状态集合 $Q$ 的幂集。设字符串 $S=x_1{x}_2\dots x_n$ 为字母表 $\Sigma$ 上的一个单词，当且仅当存在状态序列 $r_0,r_1,\dots ,r_n\in Q$ 满足下述条件时，自动机 $M$ 接受该字符串 $w$：

   $r_0=q_0$ (which means the machine starts in the start state $q_0$)
   $r_0=q_0$（表示机器从初始状态 $q_0$ 开始运行）

   $r_{i+1}\in \Delta (r_i,a_{i+1})$, for $i=0,\dots ,n-1$ (which means given each character of string S, the machine will transition from state to state according to the transition function $\Delta$)
   $r_{i+1}\in \Delta (r_i,a_{i+1})$，其中 $i=0,\dots ,n-1$（表示对于字符串 $S$ 中的每一个字符，机器都会根据转移函数 $\Delta$ 完成一次状态转移）

   $r_n\in F$ (which means the machine accepts S if the last input of S causes the machine to halt in one of the accepting states).
   $r_n\in F$（表示若字符串 $S$ 的最后一个输入字符使机器终止于某一接受状态，则该字符串 $S$ 被机器接受）

4. $q_0$: It is the initial state (which may be fixed or variable depending on machine behavior). $q_0\in Q$
   $q_0$：表示初始状态，其是否固定取决于自动机的运行机制，满足 $q_0\in Q$。

5. F: It is the set of final states ($F\subseteq Q$). It is assumed here that there may be more than one final state.
   $F$：表示终止状态集合，满足 $F\subseteq Q$。本定义中允许存在多个终止状态。

Representation of NFAs:

非确定性有限自动机的表示方法

A NFAs can be represented by the following ways;
非确定性有限自动机可通过以下三种方式表示：

1. Transaction diagram NFA or State diagram
   转移图（又称状态图）

2. Transaction table NFA
   转移表

3. Language of NFA
   非确定性有限自动机对应的语言

Transaction diagram of NFA:

非确定性有限自动机的转移图

Transaction diagram is the graphical representation of NAFs. It is also called state diagram. To represent the behavior of a machine under NFA we are using digraph where;
转移图是非确定性有限自动机的图形化表示形式，也被称为状态图。转移图采用有向图描述非确定性有限自动机的运行行为，各元素定义如下：

• Nodes or vertices of the digraph represent the states that belong to set of states Q, and
  有向图的节点（顶点）对应状态集合 $Q$ 中的元素。

• The connected arcs or arrow labeled with an input alphabets from $\sum$ that show the transition.
  有向图的有向边（箭头）由输入字母表 $\sum$ 中的符号标记，代表状态转移关系。

• The initial state is denoted by a circle with an empty single incoming arc.
  初始状态的表示方式为：一个圆形节点，外部有一条无起点的有向边指向该节点。

• The finial state is indicated by double circles.
  终止状态采用双层圆形节点表示。

Transaction table of NFA:

非确定性有限自动机的转移表

A transaction table is a tabular representation of the behavior of transaction function $\delta$ that takes two arguments as input and returns an output state or next state. The transaction table represents all the moves of a finite semi-automata or finite state machine based on the current state and other inputs. Formally a transaction table is a 2-dimension array that consists of rows and columns where;
转移表是状态转移函数 $\delta$ 运行行为的表格化表示形式，该函数以当前状态与输入符号为两个参数，输出对应的下一状态集合。转移表可完整描述有限半自动机或有限状态机基于当前状态与输入符号的全部转移过程。形式上，转移表是一个二维数组，包含行与列两个维度，各维度定义如下：

• The columns contain the state in which the machine will be on the input alphabet $\sum$ represented by that column.
  列维度由输入字母表 $\sum$ 中的符号构成，每一列对应一个输入符号。

• The rows corresponding to the state of the finite control unit can be in or it contains the states of the finite automata machine (current state and/or next state).
  行维度对应有限控制器的状态，包含该有限自动机的全部状态（当前状态与下一状态）。

• The entry for one row corresponding to state $q_i$ and the column corresponding to input a is the state $\delta (q_i,a)$.
  行对应状态 $q_i$ 且列对应输入符号 $a$ 时，表格对应位置的元素为状态集合 $\delta (q_i,a)$。

Language of NFA:

非确定性有限自动机对应的语言

The language of NFA consist a set of all strings chosen from ${\sum }^{\ast }$ that all are accepted by machine M.
非确定性有限自动机对应的语言，是由字母表闭包 ${\sum }^{\ast }$ 中所有能被自动机 $M$ 接受的字符串构成的集合。

Example of NFA:

非确定性有限自动机实例

Represent the NFA of machine
构造如下非确定性有限自动机
M = ( { A , B , C , D } , { a , b } , δ , A , { B } ) M = (\{A, B, C, D\}, \{a, b\}, \delta, A, \{B\}) M=({A,B,C,D},{a,b},δ,A,{B}), where $\delta$ is given as;
M = ( { A , B , C , D } , { a , b } , δ , A , { B } ) M = (\{A, B, C, D\}, \{a, b\}, \delta, A, \{B\}) M=({A,B,C,D},{a,b},δ,A,{B})，其中转移函数 $\delta$ 的定义如下：
$\delta (A,a)=B$,
$\delta (A,a)=C$,
$\delta (A,a)=D$,
$\delta (C,b)=A$,
$\delta (C,b)=B$,
$\delta (D,b)=B$.

State transaction diagram of machine ‘M’:

自动机 $M$ 的状态转移图

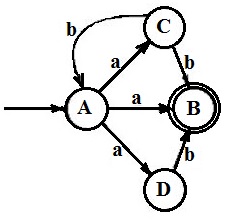
NFAs state diagram
非确定性有限自动机状态转移图

State transaction table of machine ‘M’:

自动机 $M$ 的状态转移表

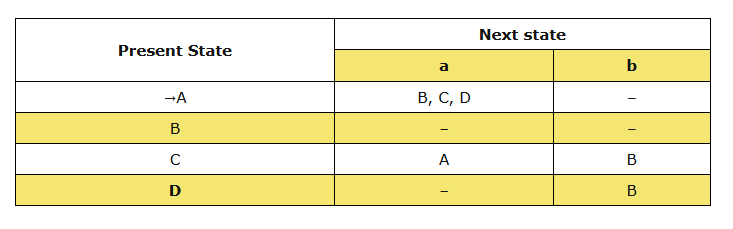
Language of NFA of machine ‘M’:
自动机 $M$ 对应的语言：
L M = { a , a b , a b ∗ b } L_M = \{ a, ab, ab^*b\} LM​={a,ab,ab∗b} or
L M = { a + a b + a b ∗ b } L_M = \{ a + ab + ab^*b\} LM​={a+ab+ab∗b} or
L M = { a + a b ∗ b } L_M = \{ a + ab^*b\} LM​={a+ab∗b}

Application of NFA:

非确定性有限自动机的应用

As we know that NFAs and DFAs are equivalent, so if a language is recognized by an NFA then it is also recognized by a DFA and vice versa. The establishment of such equivalence is important and highly applicable in various cases as follows;
我们已知非确定性有限自动机与确定性有限自动机具有等价性，即若某一语言可被非确定性有限自动机识别，则必然可被确定性有限自动机识别，反之亦然。这一等价性的证明具有重要意义，且在诸多场景中具备极高的应用价值，具体如下：

• Construction of an NFA to recognize a given language is sometimes much easier than constructing a DFA for that language.
  对于特定语言，构造其对应的非确定性有限自动机往往比构造确定性有限自动机更为简便。

• NFAs used to reduce the complexity of the mathematical work required to establish many important properties in the theory of computation.
  非确定性有限自动机可降低计算理论中诸多重要性质证明的数学推导复杂度。

• NFAs is highly applicable to prove closure properties of regular languages in much easier way compare to DFAs.
  与确定性有限自动机相比，非确定性有限自动机可更简便地用于证明正则语言的封闭性。

---

Difference Between DFA NFA | NFA Vs DFA automata

确定性有限自动机与非确定性有限自动机的区别 | 非确定性有限自动机与确定性有限自动机对比

By Er Parag Verma
Mar 20, 2016

The finite automaton or finite automata theory has several classes that include the Deterministic Finite Automata (DFA) and the Nondeterministic Finite Automata (NFA). These two classes are transition functions of finite automata or finite automata and they have some significant differences those are completely distinguish the behavior of the finite auotmata. Here two separate tables those are clearly explained the difference between the DFA and NFA and compare the performance of DFA and NFA on the behalf of various fields;
有限自动机理论包含多个类别，其中主要包括确定性有限自动机（DFA）与非确定性有限自动机（NFA）。这两类自动机的核心区别体现在状态转移函数上，这些区别决定了二者运行行为的差异。下文通过两个表格，从不同维度详细阐述确定性有限自动机与非确定性有限自动机的区别，并对比二者的性能特征。

Difference between Deterministic Finite Automata and the Non deterministic Finite Automata ((DFA Vs NFA):

确定性有限自动机与非确定性有限自动机的区别（DFA 与 NFA 对比）

S. No.	DFA	NFA
1.	For Every symbol of the alphabet, there is only one state transition in DFA. 对于字母表中的每一个符号，仅存在唯一的状态转移路径。	We do not need to specify how does the NFA react according to some symbol. 无需为字母表中的所有符号定义对应的状态转移行为。
2.	DFA cannot use Empty String transition. 不支持空串转移。	NFA can use Empty String transition. 支持空串转移。
3.	DFA can be understood as one machine. 可被理解为单台运行的机器。	NFA can be understood as multiple little machines computing at the same time. 可被理解为多台子机器并行运行。
4.	DFA will reject the string if it end at other than accepting state. 若输入字符串终止于非接受状态，则判定为拒绝该字符串。	If all of the branches of NFA dies or rejects the string, we can say that NFA reject the string. 仅当所有转移分支均终止于非接受状态时，才判定为拒绝该字符串。
5.	Backtracking is allowed in DFA. 允许回溯操作。	Backtracking is not always allowed in NFA. 不总是允许回溯操作。
6.	DFA can be understood as one machine. 可被理解为单台运行的机器。	NFA can be understood as multiple little machines computing at the same time. 可被理解为多台子机器并行运行。
7.	DFA will reject the string if it end at other than accepting or final state. 若输入字符串终止于非接受状态（非终止状态），则判定为拒绝该字符串。	If all of the branches of NFA dies or rejects the string, we can say that NFA reject the string. 仅当所有转移分支均终止于非接受状态时，才判定为拒绝该字符串。
8.	DFA is more difficult to construct. 构造难度较高。	NFA is easier to construct. 构造难度较低。
9.	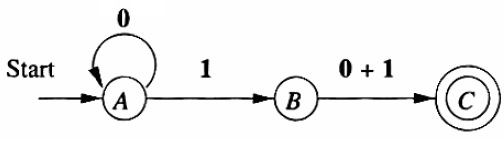确定性有限自动机实例	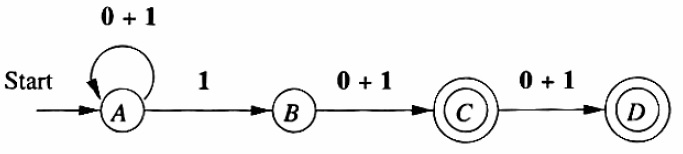非确定性有限自动机实例

Comparison between Deterministic Finite Automata (DFA) and the Nondeterministic Finite Automata (NFA):

确定性有限自动机（DFA）与非确定性有限自动机（NFA）的性能对比

DFA Vs NFA automata
确定性有限自动机与非确定性有限自动机对比

S. No.	Title	NFA	DFA
1.	Power	Same 二者相同	Same 二者相同
2.	Supremacy	Not all NFA are DFA. 并非所有非确定性有限自动机都可转化为确定性有限自动机。	All DFA are NFA. 所有确定性有限自动机均为非确定性有限自动机的特例。
3.	Transition Function	Maps Q → ( ∑ ∪ { λ } → 2 Q ) Q \to (\sum \cup \{\lambda\} \to 2^Q) Q→(∑∪{λ}→2Q), the number of next states is zero or one or more. 映射关系为 Q → ( ∑ ∪ { λ } → 2 Q ) Q \to (\sum \cup \{\lambda\} \to 2^Q) Q→(∑∪{λ}→2Q)，下一状态数量可为 0、1 或多个。	$Q\times \sum \to Q$, the number of next states is exactly one. 映射关系为 $Q\times \sum \to Q$，下一状态数量唯一。
4.	Time complexity	The time needed for executing an input string is more as compare to DFA. 处理输入字符串的耗时高于确定性有限自动机。	The time needed for executing an input string is less as compare to NFA. 处理输入字符串的耗时低于非确定性有限自动机。
5.	Space	Less space requires. 所需存储空间较少。	More space requires. 所需存储空间较多。

---

Finite Automata: example, equivalence, limitation and Application of FA

有限自动机：实例、等价性、局限性及应用

By Er Parag Verma Mar 20, 2016

A finite automata (FA) is the most restricted model of automatic machine. A finite automata is an abstract model of a computer system. As per its defining characteristics is that they have only a finite number of states. Hence, a finite automata can only “count” (that is, maintain a counter, where different states correspond to different values of the counter) a finite number of input scenarios. Hence there has some of the restriction or limitations are as follows;
有限自动机（FA）是限制条件最多的自动机模型，同时也是计算机系统的抽象模型。有限自动机的定义特征为其仅包含有限个状态，因此该模型仅能对有限种输入场景进行“计数”（即通过不同状态对应计数器的不同取值，实现计数功能）。基于上述特征，有限自动机存在如下限制与局限性：

1. The input tape is read only and the only memory it can have is by moving from state to state and since there are finite number of states, a finite automata has memory which is strictly finite.
   输入带为只读模式，有限自动机仅能通过状态转移实现记忆功能；由于状态数量有限，该模型的记忆容量严格受限。

2. The finite automata have only string pattern (regular expression) recognizing power.
   有限自动机仅具备字符串模式（正则表达式）识别能力。

3. The head movement is restricted in one direction, either from left to right or right to left.
   读写头的移动方向受限，仅能沿单一方向移动（从左至右或从右至左）。

We can modify or enhance the model of finite automata by removing one or more limitation like movement in both direction (Two way finite automata) but these enhancements do not increase the recognizing power of finite automata.
可通过解除部分限制条件对有限自动机模型进行改进或增强，例如允许读写头双向移动（即双向有限自动机），但此类改进无法提升有限自动机的识别能力。

Examples of Limitation of finite auotmata:

有限自动机局限性实例

There is no finite automaton that recognizes these strings:
不存在能够识别以下字符串集合的有限自动机：

1. The set of binary strings consisting of an equal number of a’s and b’s.
   由数量相等的字符 $a$ 与字符 $b$ 构成的二进制字符串集合。

2. The set of strings over ‘(‘ and ‘)’ that have “balanced” parentheses.
   由左括号 ( 与右括号 ) 构成的括号匹配字符串集合。

The ‘pumping lemma’ can be used to prove that no such FA exists for these examples.
可通过“泵引理”证明不存在能够识别上述字符串集合的有限自动机。

Equivalence of Finite Automata:

有限自动机的等价性

Two automata $M_0$ and $M_1$ are said to be equivalent to each other if both accept exactly the same set of input strings. Formally, if two automata $M_0$ and $M_1$ are equivalent then
若两个自动机 $M_0$ 与 $M_1$ 接受的输入字符串集合完全相同，则称这两个自动机等价。形式上，若自动机 $M_0$ 与 $M_1$ 等价，则满足以下条件：

• If there is a path from the start state of $M_0$ to a final state of $M_0$ labeled $M_{01}{M}_{02}\dots \dots M_{0k}$, there is a path from the start state of $M_1$ to a final state of $M_1$ labeled $M_{01},M_{02}......M_{0k}$.
  若存在一条从自动机 $M_0$ 初始状态到终止状态的路径，其标记为 $M_{01}{M}_{02}\dots \dots M_{0k}$，则必然存在一条从自动机 $M_1$ 初始状态到终止状态的路径，且该路径的标记同样为 $M_{01}{M}_{02}\dots \dots M_{0k}$。

• If there is a path from the start state of $M_1$ to a final state of $M_1$ labeled $M_{11},M_{12}\dots .....\dots .M_{1k}$, there is a path from the start state of $M_0$ to a final state of $M_0$ labeled $M_{11},M_{12},\dots \dots ..M_{1k}$.
  若存在一条从自动机 $M_1$ 初始状态到终止状态的路径，其标记为 $M_{11}{M}_{12}\dots \dots M_{1k}$，则必然存在一条从自动机 $M_0$ 初始状态到终止状态的路径，且该路径的标记同样为 $M_{11}{M}_{12}\dots \dots M_{1k}$。

Application of Finite Automata (FA):

有限自动机（FA）的应用

We have several application based on finite automata and finite state machine. Some are given below;
有限自动机与有限状态机具有诸多应用场景，部分场景如下：

• A finite automata is highly useful to design Lexical Analyzers.
  可用于设计词法分析器。

• A finite automata is useful to design text editors.
  可用于设计文本编辑器。

• A finite automata is highly useful to design spell checkers.
  可用于设计拼写检查器。

• A finite automata is useful to design sequential circuit design (Transducer).
  可用于设计时序逻辑电路（转换器）。

---

NFA to DFA conversion algorithm with solved example

非确定性有限自动机转确定性有限自动机算法及实例解析

By Er Parag Verma
Mar 20, 2016

Finite automata include two different classes Deterministic Finite Automata (DFA) and the Non deterministic Finite Automata (NFA). These are converted from one to another i.e. Non-Deterministic Finite Automata to Deterministic Finite Automata (NFA to DFA) conversion and Deterministic Finite Automata to Non-Deterministic Finite Automata (DFA to NFA) conversion. Some more enhancement of the NFA machine is NFA with ε moves i.e. (ε-NFA) can be converted into DFA and vice versa. A DFA is directly converted into a Regular expression. The below diagram explains all conversions of Finite Automata conversion.
有限自动机包含两个主要类别，分别为确定性有限自动机（DFA）与非确定性有限自动机（NFA）。这两类自动机可相互转化，即实现非确定性有限自动机到确定性有限自动机的转化（NFA 转 DFA），以及确定性有限自动机到非确定性有限自动机的转化（DFA 转 NFA）。非确定性有限自动机的增强模型——带空转移的非确定性有限自动机（ε-NFA）同样可与确定性有限自动机相互转化。此外，确定性有限自动机可直接转化为正则表达式。下图展示了有限自动机的各类转化关系。

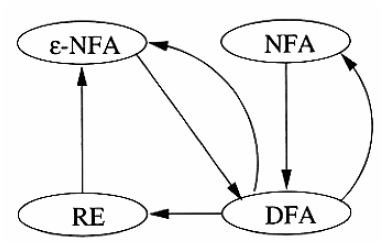
非确定性有限自动机转确定性有限自动机及确定性有限自动机转非确定性有限自动机的转化框图

Figure (1) : (NFA→ DFA) and (DFA→ NFA) conversion block diagram
图 1：非确定性有限自动机与确定性有限自动机之间的转化框图

Non Deterministic Finite Automata to Deterministic Finite Automata (NFA to DFA conversion) :

非确定性有限自动机转确定性有限自动机（NFA 转 DFA）

The goal is to construct a Deterministic Finite Automata (DFA) from a given Non-Deterministic Finite Automata (DFA) machine which is much faster in recognition of an input string. The main idea behind this conversion is to construct a DFA machine in which each state will correspond to a set of NFA states.
该转化的目标是，基于给定的非确定性有限自动机（NFA）构造等价的确定性有限自动机（DFA），以提升输入字符串的识别效率。转化的核心思想为：构造的确定性有限自动机中，每个状态对应原非确定性有限自动机的一个状态集合。

Worst Case complexity of (NFA→ DFA) conversion:

非确定性有限自动机转确定性有限自动机的最坏时间复杂度

The worst-case complexity of NFA to DFA conversion is $O(2^N)$ of sets of states. The DFA can have exponentially many more states than the NFA in rare cases.
非确定性有限自动机转确定性有限自动机的最坏时间复杂度为 $O(2^N)$（$N$ 为原非确定性有限自动机的状态数量）。在极端情况下，转化得到的确定性有限自动机的状态数量会以指数形式多于原非确定性有限自动机的状态数量。

NFA to DFA conversion Algorithm:

非确定性有限自动机转确定性有限自动机的算法

Input:
输入

A NFA S = States = { s 0 , s 1 , … , s N } = S N F A S = \text{States} = \{ s_0, s_1, …, s_N\} = S_{NFA} S=States={s0​,s1​,…,sN​}=SNFA​
非确定性有限自动机 S = 状态集合 = { s 0 , s 1 , … , s N } = S N F A S = \text{状态集合} = \{ s_0, s_1, …, s_N\} = S_{NFA} S=状态集合={s0​,s1​,…,sN​}=SNFA​

$\delta =\text{Move function}={\text{Move}}_{NFA}$
$\delta =\text{转移函数}={\text{Move}}_{NFA}$

${\text{Move}}^{\prime }(S,a)\to \text{Set of states}$
${\text{Move}}^{\prime }(S,a)\to \text{状态集合}$

Output:
输出

A DFA S = States = { ? , ? , … , ? } = S D F A S = \text{States} = \{?, ?, …, ?\} = S_{DFA} S=States={?,?,…,?}=SDFA​
确定性有限自动机 S = 状态集合 = { ? , ? , … , ? } = S D F A S = \text{状态集合} = \{?, ?, …, ?\} = S_{DFA} S=状态集合={?,?,…,?}=SDFA​

$\delta =\text{Move function}={\text{Move}}_{DFA}$
$\delta =\text{转移函数}={\text{Move}}_{DFA}$

$\text{Move}(s,a)\to \text{Single state from }{S}_{DFA}$
$\text{Move}(s,a)\to S_{DFA}\text{ 中的单一状态}$

Main idea:
核心思想

Each state in $S_{DFA}$ will be a set of states from the NFA S D F A = { { … } , { … } , … , { … } } S_{DFA} = \{ \{…\}, \{…\}, …, \{…\} \} SDFA​={{…},{…},…,{…}}
$S_{DFA}$ 中的每个状态对应原非确定性有限自动机的一个状态集合，即 S D F A = { { … } , { … } , … , { … } } S_{DFA} = \{ \{…\}, \{…\}, …, \{…\} \} SDFA​={{…},{…},…,{…}}
(The name of the states in constructed DFA is arbitrary and can be changed later if desired.)
（构造得到的确定性有限自动机的状态名称可任意设定，后续可根据需求修改）

Method:
方法
Construct a transition table TransitionD. Each DFA state is a set of NFA states. TransitionD simulates in parallel all possible moves N can make on a given string.
构造转移表 ${\text{Transition}}_D$，其中确定性有限自动机的每个状态对应原非确定性有限自动机的一个状态集合。该转移表可并行模拟原非确定性有限自动机在给定输入字符串上的所有可能转移路径。

Operations to keep track of sets of NFA states:
用于追踪非确定性有限自动机状态集合的操作：
ε Closure (S):
ε 闭包（$S$）
Set of states reachable from state S via epsilon.
从状态 $S$ 出发，通过任意次空转移可到达的所有状态的集合。

ε Closure (T):
ε 闭包（$T$）
Set of states reachable from any state in set T via epsilon.
从集合 $T$ 中的任意状态出发，通过任意次空转移可到达的所有状态的集合。

move (T, a):
转移操作（$T,a$）
Set of states to which there is an NFA transition from states in T on a symbol a.
从集合 $T$ 中的任意状态出发，通过输入符号 $a$ 可直接转移到的所有状态的集合。

Algorithm:

算法步骤

initially, ε-Closure ($S_0$) in TransitionD.
初始化，将 $\epsilon \text{-Closure}(S_0)$ 加入转移表 ${\text{Transition}}_D$。

While unmarked state T in TransitionD
遍历转移表 ${\text{Transition}}_D$ 中未标记的状态 $T$
mark T
标记状态 $T$

for each input symbol ‘a’
遍历每个输入符号 $a$

do $u=\epsilon \text{ Closure }(\text{move}(T,a))$
计算 $u=\epsilon \text{ 闭包}(\text{转移操作}(T,a))$

If u is not in TransitionD
若 $u$ 未包含于转移表 ${\text{Transition}}_D$

then add u to TransitionD
则将 $u$ 加入转移表 ${\text{Transition}}_D$

Transition $[T,a]=u$
设置转移关系 $\text{Transition}[T,a]=u$

The following algorithm shows a computation of ε -Closure function.
下述算法描述 ε 闭包函数的计算过程

Push all states in T onto the stack.
将集合 $T$ 中的所有状态压入栈中

initialize ε-Closure (T) to T
初始化 $\epsilon \text{-Closure}(T)=T$

while the stack is not empty
当栈不为空时

do pop top element t
弹出栈顶元素 $t$

for each state u with ε-edge t to u
遍历所有满足条件的状态 $u$：存在从 $t$ 到 $u$ 的空转移边

do If u is not in ε-Closure(T)
若 $u$ 未包含于 $\epsilon \text{-Closure}(T)$

do add u ε Closure (T)
将 $u$ 加入 $\epsilon \text{-Closure}(T)$

push u onto the stack
将 $u$ 压入栈中

注： “u s.t. t ‑‑ε‑‑> u”
“所有满足‘存在一条从 t 出发、标记为 ε 的边指向它’的状态 u”。或者表达为把 t 的所有 ε-后继 逐个拎出来，后面算法要对这些 u 一一处理。

1. u
   “状态”节点
2. s.t.
   “such that” ，“满足以下条件”。
3. t ‑‑ε‑‑> u
   一条从状态 t 到状态 u 的 ε-edge（空转移边）。
   强调“不消耗任何输入符号”就能从 t 跳到 u。

Remarkable Steps to convert NFA→ DFA:

非确定性有限自动机转确定性有限自动机的步骤

1. Construct the transition table of the given NFA machine.
   构造给定非确定性有限自动机的转移表。

2. Scan the next states column in the transition table from the initial state to the final state.
   从初始状态到终止状态，遍历转移表的“下一状态”列。

3. If any of the next states consists of more than one state on the single input alphabet. Then merge them and make it a new state. Place this newly constructed state in the DFA transition table as the present state.
   若某一输入符号对应的下一状态包含多个元素，则将这些元素合并为一个新状态，并将该新状态作为确定性有限自动机转移表的当前状态。

4. The next state of this newly constructed state on the input alphabet will be the summation of each next state which parts in the NFA transition table.
   对于该新状态，其在某一输入符号下的下一状态，为原非确定性有限自动机转移表中对应状态集合内各元素在该输入符号下的下一状态的并集。

5. Repeat steps 2 to step 4 until all the states in the NFA transition table will be scanned completely.
   重复步骤 2 至步骤 4，直至遍历完原非确定性有限自动机转移表中的所有状态。

6. The final transition table must have a single next state at a single input alphabet.
   最终得到的转移表中，每个当前状态在单一输入符号下对应的下一状态必须唯一。

Example:
实例

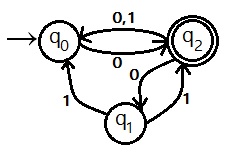
非确定性有限自动机转确定性有限自动机实例

Figure (1): NFA
图 1：非确定性有限自动机

Construct the equivalent DFA of the NFA given in figure (1).
构造图 1 所示非确定性有限自动机的等价确定性有限自动机
Step 1: Transition Table of NFA from Figure (1):
步骤 1：构造图 1 所示非确定性有限自动机的转移表

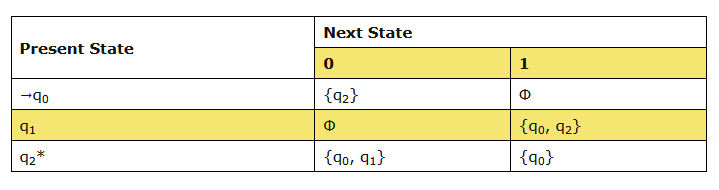
Step 2: Transition Table of DFA:
步骤 2：构造等价确定性有限自动机的转移表

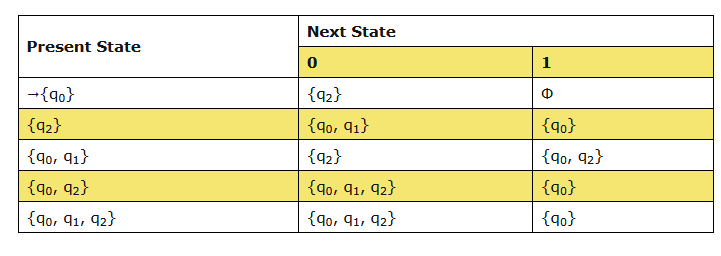
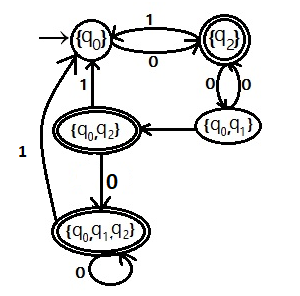
非确定性有限自动机转确定性有限自动机

---

via:

• DFA : definition, representations, application ( Deterministic Finite Automata ) | Engineer’s Portal
  https://er.yuvayana.org/dfa-definition-representations-application-deterministic-finite-automata/
• NFA: Nondeterministic Finite Automata Definition, Example, Application | Engineer’s Portal
  https://er.yuvayana.org/nfa-nondeterministic-finite-automata-definition-example-application/
• Difference Between DFA NFA | NFA Vs DFA automata……
  https://er.yuvayana.org/difference-between-dfa-nfa-nfa-vs-dfa-automata/
• NFA to DFA conversion algorithm with solved example
  https://er.yuvayana.org/nfa-to-dfa-conversion-algorithm-with-solved-example/
• Finite Automata: example, equivalence, limitation and Application of FA | Engineer’s Portal
  https://er.yuvayana.org/finite-automata-example-equivalence-limitation-and-application-of-fa/
• automata theory languages and computation tutorial | Engineer’s Portal
  https://er.yuvayana.org/tag/automata-theory-languages-and-computation-tutorial/