目录
上篇在这:
1.代数结构

对于任意x,y属于自然数集都能进行加法运算,并且运算结果唯一。运算的结果也属于自然数集,所以这个运算是自然数集上的二元运算。
下面这个运算,运算结果也唯一,但是两个自然数相减,最后得到的结果可能是一个负数,而负数不属于自然数,所以这个运算不是自然数集上的二元运算。



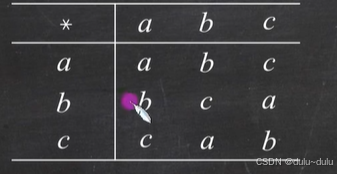
左幺元:左幺元*x=x,所以将每一行与列元素比较,如果相同就是左幺元。所以下图中,a是左幺元。
右幺元:x*右幺元=x,所以以列为单位,判断每一列是否和行元素相同,所以下图,a是右幺元。
所以a是幺元。
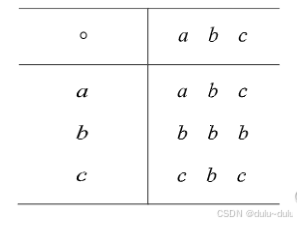
左零元:左零元*x=左零元,如下图第一行元素a,b,c。只有a与行相同,下面两列同理,所以a,b,c都不是左零元,所以都不是零元。
逆元:b*a=幺元a a*b=幺元a。
所以:
第二幅图同理:
2.群
代数系统:
非空集合S和S上k个一元或者二元运算组成的系统,如<N,+>(自然数集上的加法运算),<Z,+,x>(整数集上的加法运算和乘法运算)
二元运算上面已经讲过,就是结果唯一,并且结果在集合中。
广群,半群,独异点:

半群也可以理解为:① 代数系统 ② 二元运算是封闭的 ③ 二元运算是可结合的
独异点:① 代数系统 ② 二元运算是封闭的 ③ 二元运算是可结合的 ④ 有幺元
若独异点中∀x∈S,存在它的逆元
,则称<S,x>是一个群。

证明代数系统是群,即要证明:

为什么幺元是1/8:
左幺元*x=x,对应到
,即b=8ab,a=1/8。同理右幺元=1/8。
a,b运算结果为1/8,所以对于集合
的任意元素a,都存在逆元。
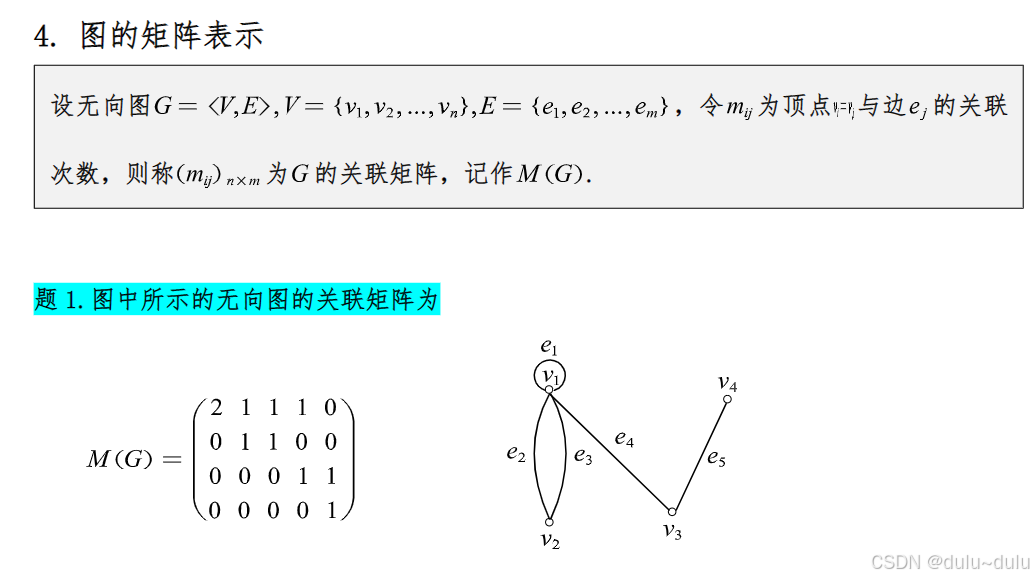
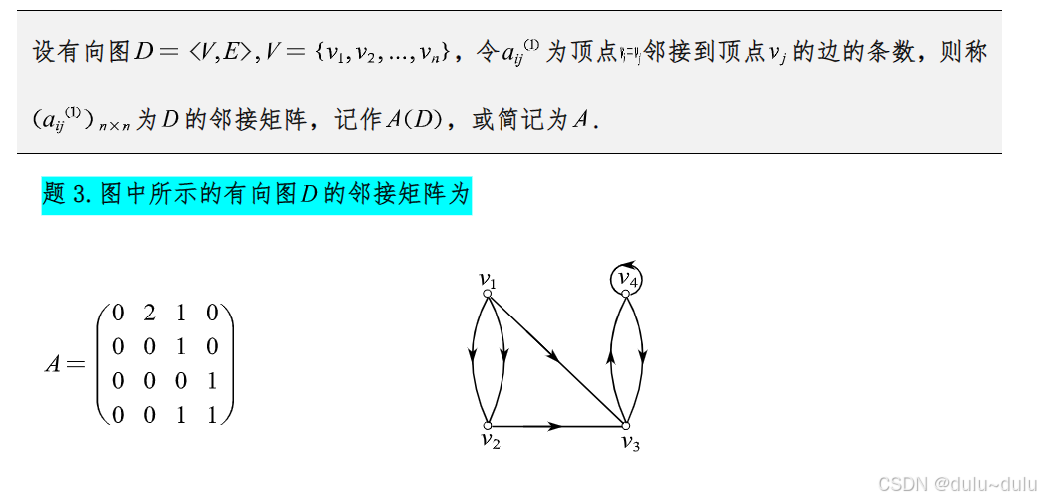
3.图
对于图,树,如果想学习得更加细致些,可以搜索数据结构的图,树两章进行学习。


任何图中,奇度顶点的个数是偶数:
度数之和 = 奇度顶点的度数之和 + 偶度顶点的度数之和
偶度顶点表示这个顶点的度数为偶数,不管都度顶点有几个,其和一定为偶数。度数之和为边数的2倍,一定为偶数,所以奇度顶点的度数之和为偶数。







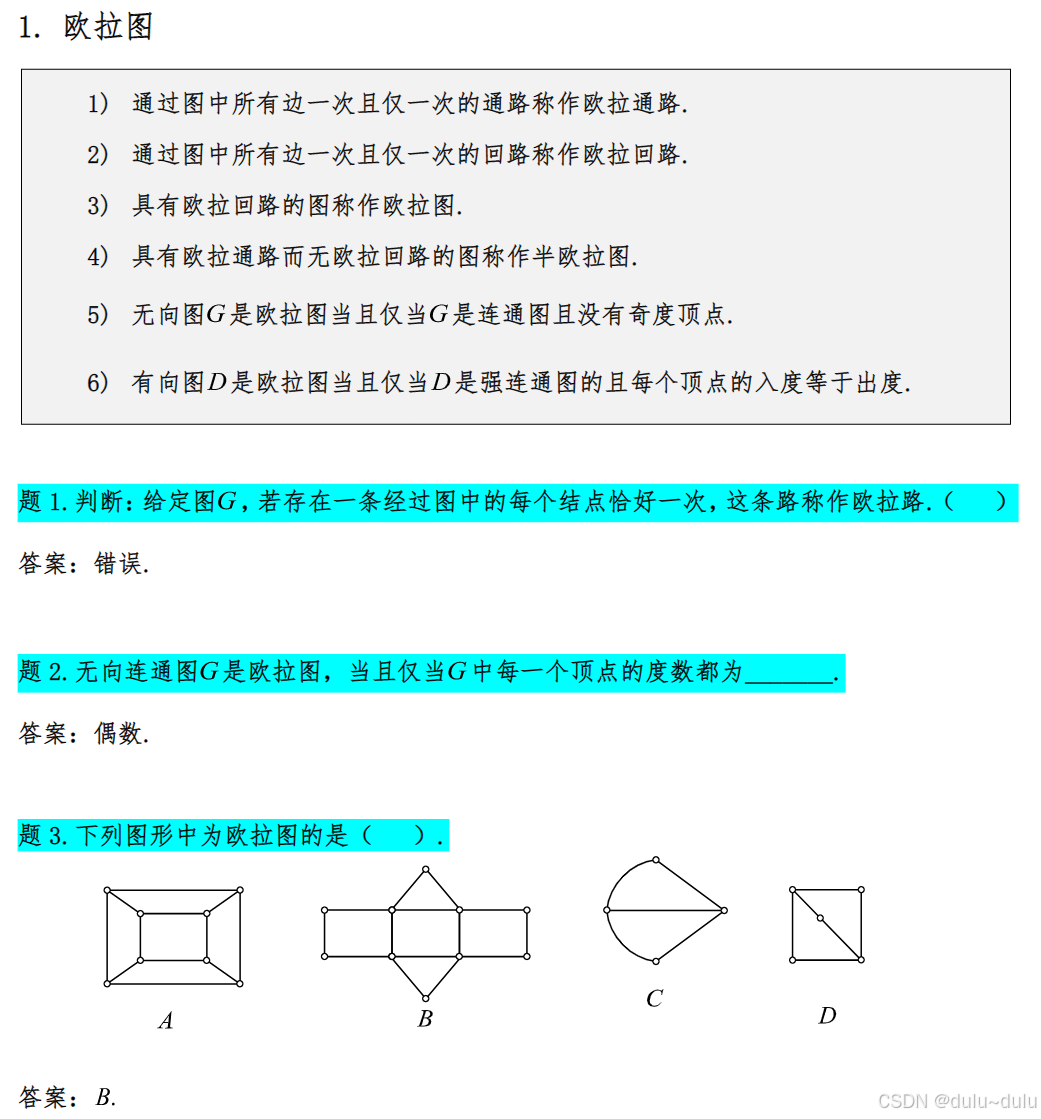
4.欧拉图和哈密顿图

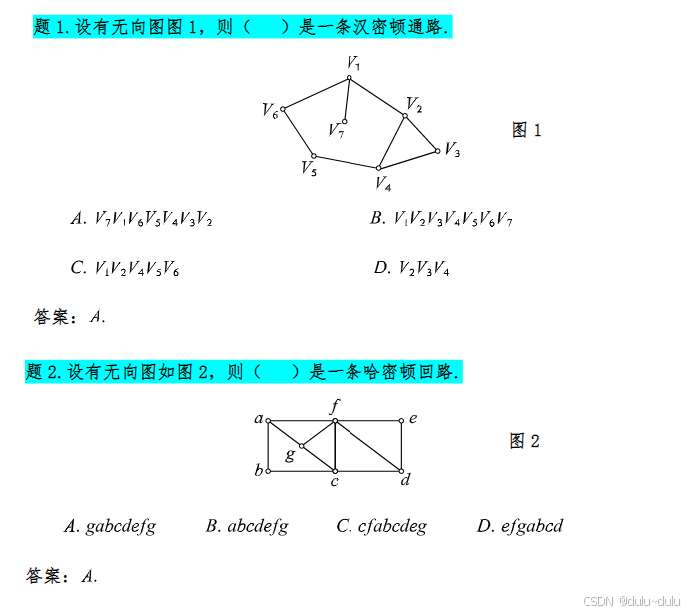

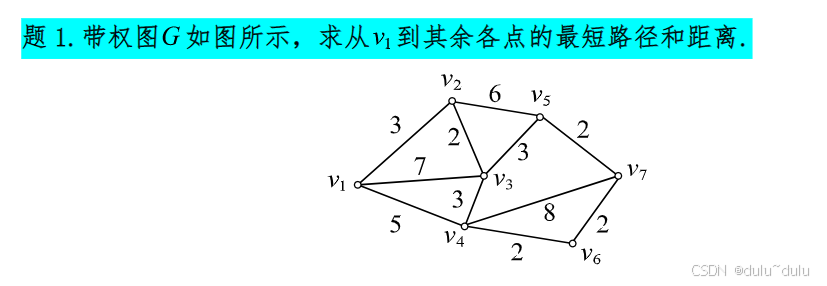
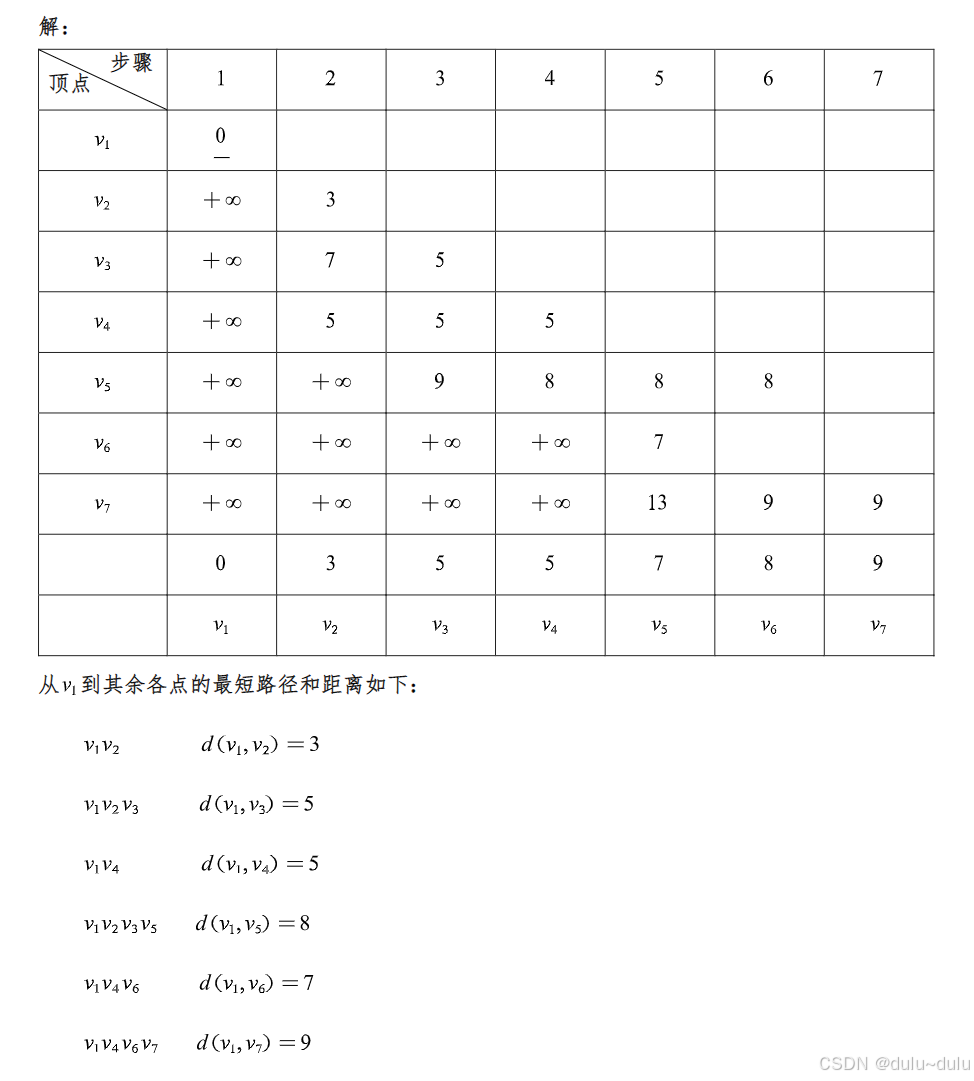
注:以上问题就是数据结构中的Dijkstra问题,如果不懂可以搜索Dijkstra更加细致的看一下。
5.树



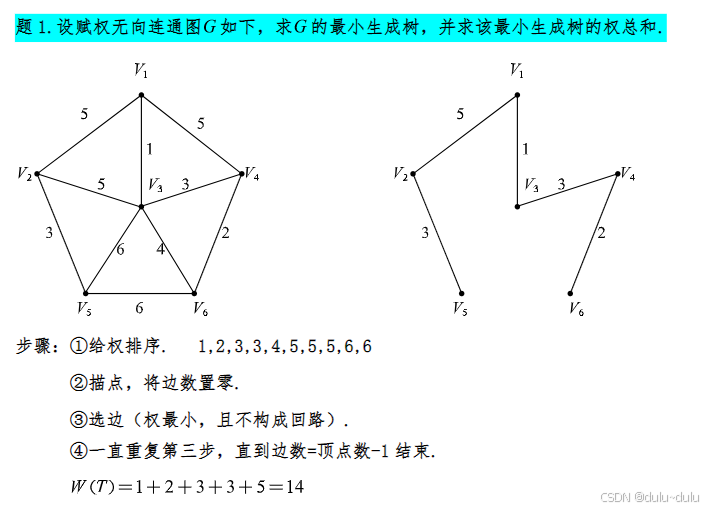

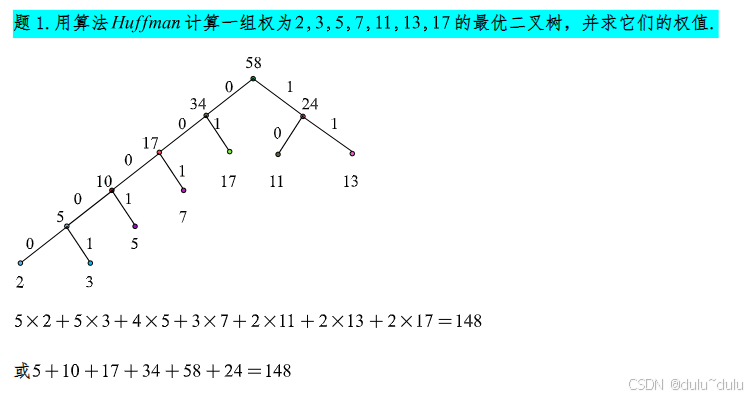


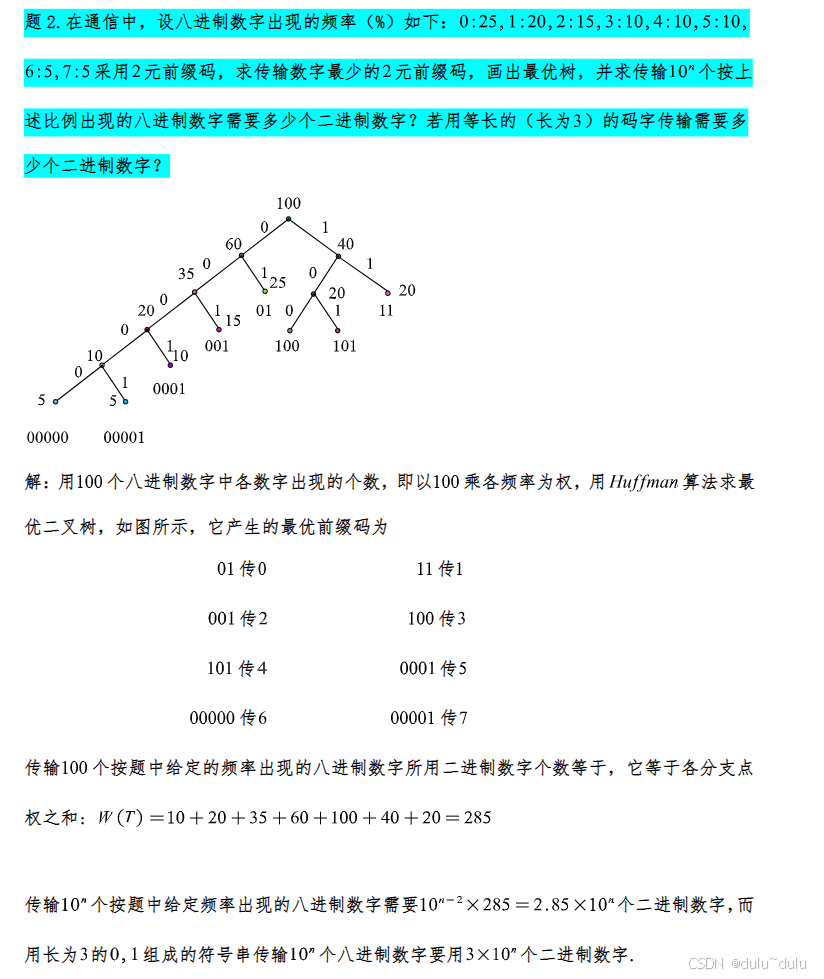
6.平面图

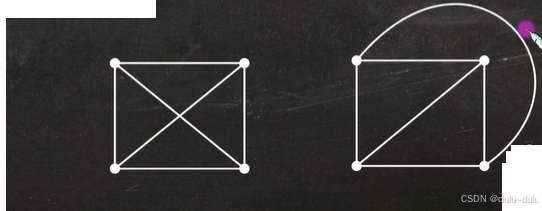
在第1个图中,将上面3个顶点看作v1,下面3个顶点看作v2。图中每一条边的两个顶点都是一个属于上面一个属于下面,所以第1个图是一个二部图。但是不满足v1的每个顶点都与v2的每个顶点相邻,所以其不是完全二部图。第2个就是完全二部图。
 、
、
注:K1表示顶点为1的完全图(一个图有n个顶点,那么如果任意两个顶点之间都有边的话,该图就称为完全图),K2表示顶点为2的完全图,以此类推。
如下图,K4如果将一边往外拉,可以使得没有边相交,所以K4是平面图

例如,三角形能够将两个平面划分为三角形内部和外部,所以三角形有两个面,边界长度为3(3条边),面的次数为3。

更加细致地学习,可以看看:《离散数学》知识点详解:平面图II(k33和k5)_哔哩哔哩_bilibili
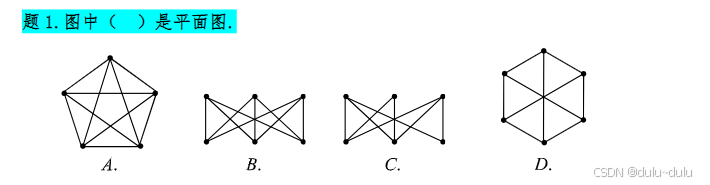
A,B项是K5和
,是极小非平面图。C项是B项删除1条边,所以C项是平面图。对于D:
无论怎么拉都有边相交,所以D不是平面图。
再举个例子:
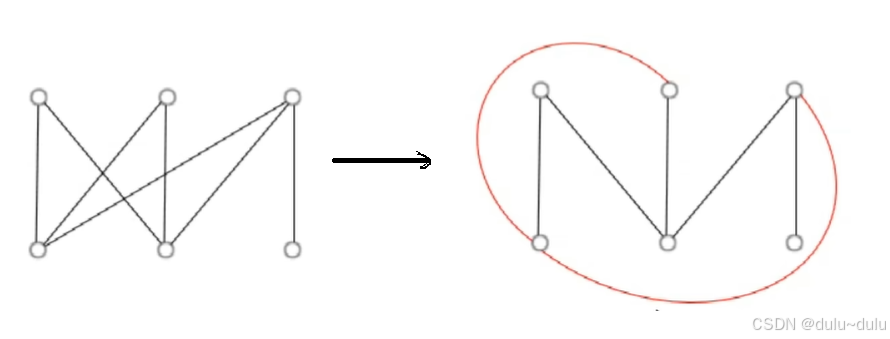
第1个图可以拉伸为第2个图,即无边相交,所以这个图是平面图。

注:区域面积无限的面称为无限面。无限面只有一个。
因为平面图所有面的次数之和等于边数的两倍:
面数之和为r,无限面占1,其余面占r-1,所以有:所有面的次数=5+3(r-1)
5+3(r-1)=2m










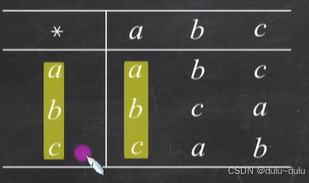
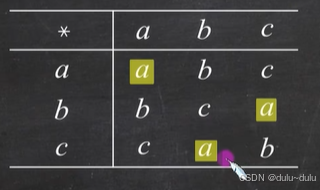
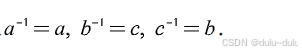


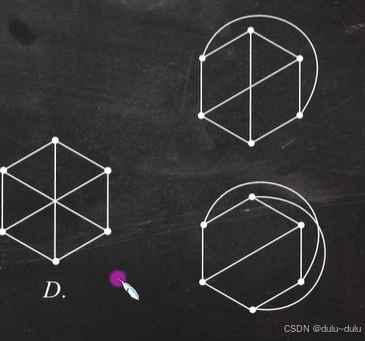
















 1173
1173

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








