目录
需要掌握:
1.K-近邻法分类预测模型的建立:
modelKNN=neighbors.KNeighborsClassifier(n_neighbors=K);
modelKNN.fit(X,Y);
modelKNN.predict(X)
2.加权K-近邻法分类预测模型的建立:
#weight为uniform(默认值),常取distance,也就是“倒数加权”,也可以自定义,下面代码中会举例
modelKNN=neighbors.KNeighborsClassifier(n_neighbors=K,weight=");
modelKNN.fit(X,Y);
modelKNN.predict(X)
3.K-近邻法的回归预测模型的建立
KNNregr=neighbors.KNeighborsRegressor(n_neighbors=K);
KNNregr.fit(X,Y)
(一)K-近邻法
1.K-近邻法的特点
一般线性模型、广义线性模型以及贝叶斯分类器都是数据预测建模的常用方法。这些方法的共同特点是需要满足某些假定。例如,一般线性模型需假定输入变量全体和输出变量具有线性关系;广义线性模型中的Logistic 回归模型需假定输入变量全体和LogitP具有线性关系;朴素贝叶斯分类器需假定输入变量条件独立。计算数据似然时,需假定数值型输入变量服从高斯分布,离散型输入变量服从多项式分布等。如果无法确定假定能否满足,就可以用近邻分析法。
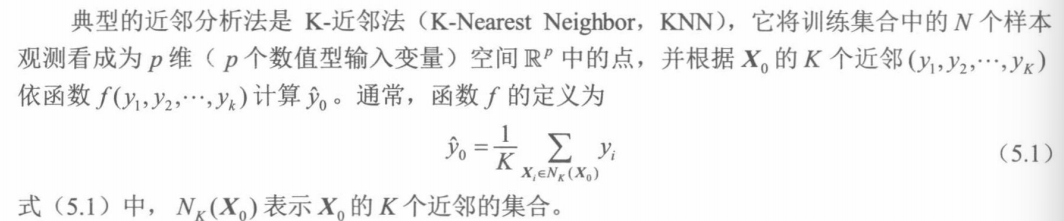
要在空间中需要定义某距离,并依此作为测度样本观测点与X0近邻关系的依据。常用的距离如下:


根据计算得到的Xi与X0的距离,判断其是否与X0有近邻关系,距离小,则与X0具有相似性,存在近邻关系。
那么多少个距离X0最近的样本需要用来参与对y0的预测,也就是如何确定K:
如上图所示,以X0为圆心。上图左图所示为1-近邻法,其错判率不会高于贝叶斯分类器错判率的2倍。 1-近邻法简单且预测精度高,但由于只依据单个近邻类别进行预测,预测结果受近邻差异的影响较大。
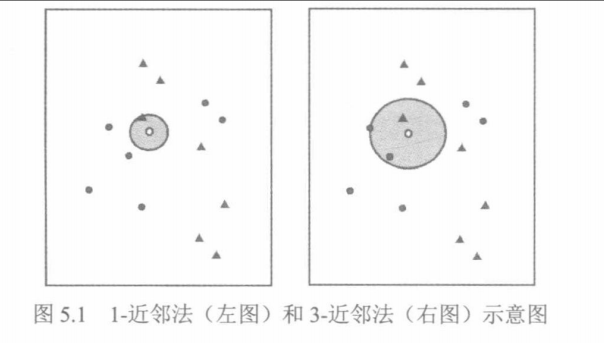
K-近邻法相对于1-近邻法而言训练误差越来越大,如下图所示,图中的圆圈和加号分别表示输出变量的两个类别(0类和1类)。深色区域和浅色区域的边界为分类边界(分类线)。若样本观测点落入深色区域,类别值预测为0。落入浅色区域类别值预测为1。可见,除左上图的1-近邻法之外,其他三幅图中均存在预测错误的点。
所以,1-近邻法特别适用于样本观测的实际类别边界极不规则的情况。随着K-近邻法参数K由小变大,分类边界越来越趋于规则和平滑,边界不再“紧随数据点”,模型复杂度由高到低,训练误差由小到大。例如,本例中5-近邻法的训练误差为16%,30-近邻法为22%,49-近邻法为 26%。
当训练集出现随机变动时,因1-近邻法“紧随数据点”,预测偏差应该仍是最小的。同时,由于其分类边界对训练集变化最为“敏感”,很可能导致预测结果(尤其是对处在分类边界附近的点)随训练集的随机变动而变动,即预测方差较大,鲁棒性低。训练集的随机变动对参数K很大的K-近邻法影响不大,其鲁棒性高但预测偏差较大。
参数K不能过小或过大。过小则模型复杂度高,很可能出现模型过拟合。过大则模型太简单,很可能出现模型欠拟合,预测性能低下。
应如何选择模型呢?答案是:可采用旁置法或 K 折交叉验证法,找到测试误差最小下的参数K。以测试误差作为模型选择的依据,是为了避免模型过拟合问题。对于 K-近邻法,测试误差是指对测试集的每个样本观测寻找其在训练集中的K个近邻,预测并计算得到的误差。
上图代码:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import sklearn.linear_model as LM
from sklearn.metrics import classification_report
from sklearn.model_selection import cross_validate,train_test_split
from sklearn import neighbors,preprocessing
np.random.seed(123)
N=50
n=int(0.5*N)
X=np.random.normal(0,1,size=100).reshape(N,2)
Y=[0]*n+[1]*n
X[0:n]=X[0:n]+1.5
X1,X2 = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),100), np.linspace(X[:,1].min(),X[:,1].max(),100))
data=np.hstack((X1.reshape(10000,1),X2.reshape(10000,1)))
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(15,12))
for K,H,L in [(1,0,0),(5,0,1),(30,1,0),(49,1,1)]:
modelKNN=neighbors.KNeighborsClassifier(n_neighbors=K)
modelKNN.fit(X,Y)
Yhat=modelKNN.predict(data)
for k,c in [(0,'silver'),(1,'red')]:
axes[H,L].scatter(data[Yhat==k,0],data[Yhat==k,1],color=c,marker='o',s=1)
axes[H,L].scatter(X[:n,0],X[:n,1],color='black',marker='+')
axes[H,L].scatter(X[(n+1):N,0],X[(n+1):N,1],color='magenta',marker='o')
axes[H,L].set_title("%d-近邻分类边界(训练误差:%.2f)"%((K,1-modelKNN.score(X,Y))))
axes[H,L].set_xlabel("X1")
axes[H,L].set_ylabel("X2")
plt.show()K-近邻法适用于实际类别边界或回归线不规则的情况下的分类预测和回归预测,同时适用于输入变量空间维度较低的情况:
K-近邻法是一种基于以X0为圆心、较短长度为半径的邻域圆(或球)的局部方法。当空间维度较低时,大数据集下样本观测在空间中分布的密集程度高于小样本,会有更多的样本观测点进入X0的邻域并参与预测,从而弱化样本观测点随机变动对预测的影响。随着空间维度p的增加,K-近邻法基于“邻域”的局部性特征将逐渐丧失,从而导致预测误差增大。
2.与朴素贝叶斯分类器和Logistic回归模型的对比
(1)K-近邻法的模型复杂度更高(K较小时),更适合解决非线性分类问题。
(2)无论朴素贝叶斯分类器还是Logistic回归模型,都是基于训练集的全部样本观测,估计预测模型的参数并根据所得模型完成预测。而K-近邻法仅基于部分样本观测直接完成预测,是一种基于以X0为圆心、较短长度为半径的邻域圆(或球)的局部方法。
(二)加权K-近邻法
加权K-近邻法的权重是Xi的权重,权重值的大小取决于X0与Xi的相似性。将相似性定义为X0与Xi距离的某种非线性函数。距离越近,X0与Xi的相似性越强,权重值越高,预测时的影响力度越大。
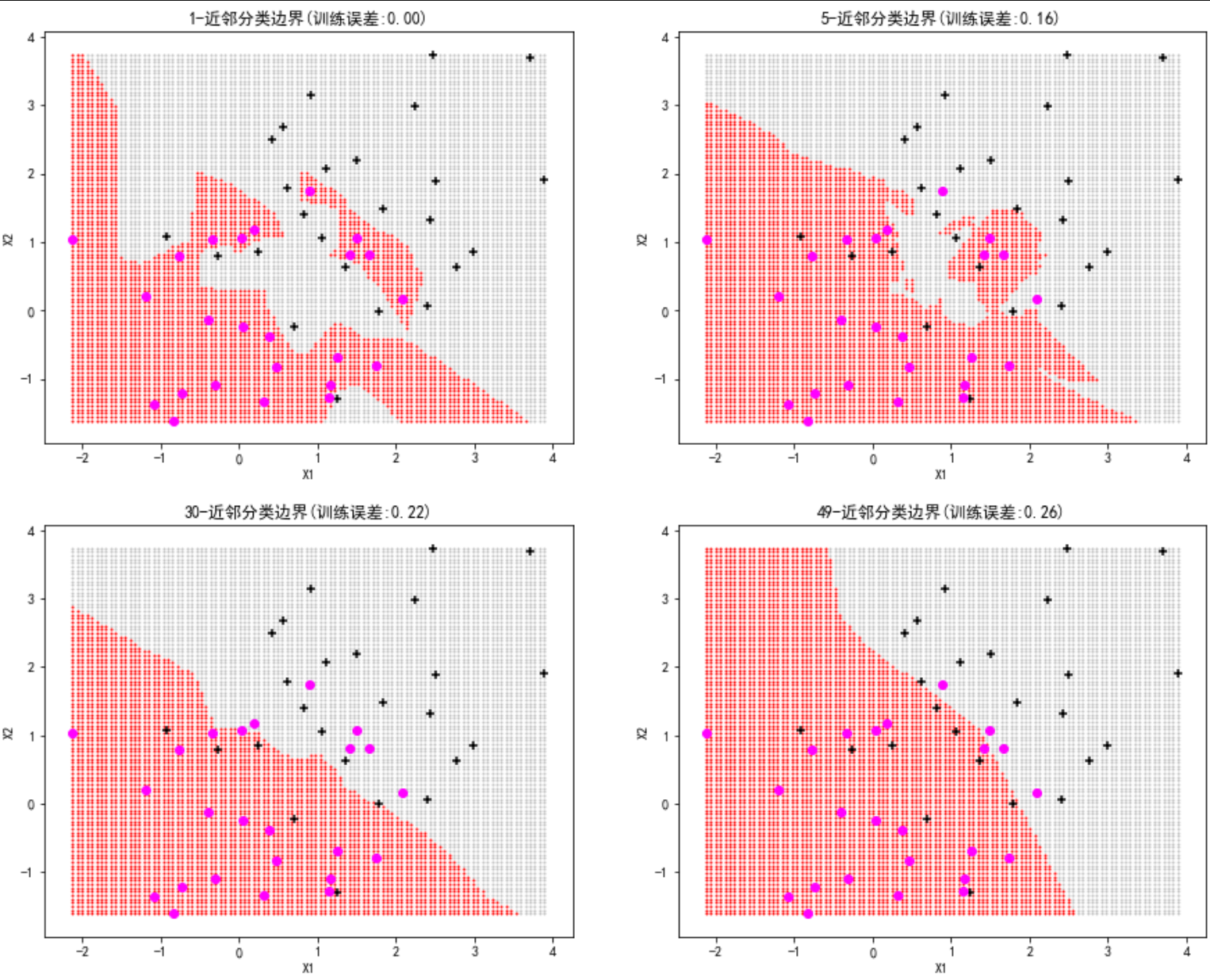
下图采用倒数加权以及高斯核函数加权,绘制加权的30-近邻法和40-近邻法的分类边界。
可以看到,与K-近邻的图相比,采用倒数加权的 30-近邻法的分类边界(左上图)不规则,且浅色和深色分别在对方区域中“开辟”了属于自己的新区域,训练误差得到有效降低,与普通1-近邻法比肩。采用高斯核函数加权的30-近邻法(右上图),训练误差也有所下降,降低到 20%。加权40-近邻法也有类似的特点。
可以看到,这里的加权K-近邻法,不仅预测效果与普通1-近邻法持平,较为理想,而且更重要的是,能够有效克服1-近邻法方差大、鲁棒性低的不足。
代码如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import sklearn.linear_model as LM
from sklearn.metrics import classification_report
from sklearn.model_selection import cross_validate,train_test_split
from sklearn import neighbors,preprocessing
#首先对距离进行标准化处理,然后计算相应的高斯密度函数值。这里指定高斯核函数中的示性函数I()等于1
def guass(x):
x=preprocessing.scale(x)
output=1/np.sqrt(2*np.pi)*np.exp(-x*x/2)
return output
np.random.seed(123)
N=50
n=int(0.5*N)
X=np.random.normal(0,1,size=100).reshape(N,2)
Y=[0]*n+[1]*n
X[0:n]=X[0:n]+1.5
X1,X2 = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),100), np.linspace(X[:,1].min(),X[:,1].max(),100))
data=np.hstack((X1.reshape(10000,1),X2.reshape(10000,1)))
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(15,12))
for W,K,H,L,T in [('distance',30,0,0,'倒数加权'),(guass,30,0,1,'高斯加权'),('distance',40,1,0,'倒数加权'),(guass,40,1,1,'高斯加权')]:
modelKNN=neighbors.KNeighborsClassifier(n_neighbors=K,weights=W)
modelKNN.fit(X,Y)
Yhat=modelKNN.predict(data)
for k,c in [(0,'silver'),(1,'red')]:
axes[H,L].scatter(data[Yhat==k,0],data[Yhat==k,1],color=c,marker='o',s=1)
axes[H,L].scatter(X[:n,0],X[:n,1],color='black',marker='+')
axes[H,L].scatter(X[(n+1):N,0],X[(n+1):N,1],color='magenta',marker='o')
axes[H,L].set_xlabel("X1")
axes[H,L].set_ylabel("X2")
axes[H,L].set_title("%d-近邻分类边界-%s(训练误差%.2f)"%((K,T,1-modelKNN.score(X,Y))))
plt.show()
(三)空气质量等级的分类预测
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import sklearn.linear_model as LM
from sklearn.metrics import classification_report
from sklearn.model_selection import cross_validate,train_test_split
from sklearn import neighbors,preprocessing
data=pd.read_excel('北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
X=data.loc[:,['PM2.5','PM10','SO2','CO','NO2','O3']]
Y=data.loc[:,'质量等级']
testPre=[] #存储不同K值对应的测试精度
#采用旁置法,训练集占70%,测试集占30%
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.70, random_state=123)
Ntrain=len(Y_train)
#从1开始,步长为10,最大为样本量20%
K=np.arange(1,int(Ntrain*0.20),10)
for k in K:
modelKNN=neighbors.KNeighborsClassifier(n_neighbors=k,weights='distance') #采用倒数加权,近邻权重随距离变远而降低
modelKNN.fit(X_train,Y_train)
testPre.append(modelKNN.score(X_test,Y_test))
plt.figure(figsize=(9,6))
plt.grid(True, linestyle='-.')
plt.xticks(K)
plt.plot(K,testPre,marker='.')
plt.xlabel("K")
plt.ylabel("测试精度")
bestK=K[testPre.index(np.max(testPre))]
plt.title("加权K-近邻的测试精度(1-测试误差)变化折线图\n(最优参数K=%d)"%bestK)
输出:
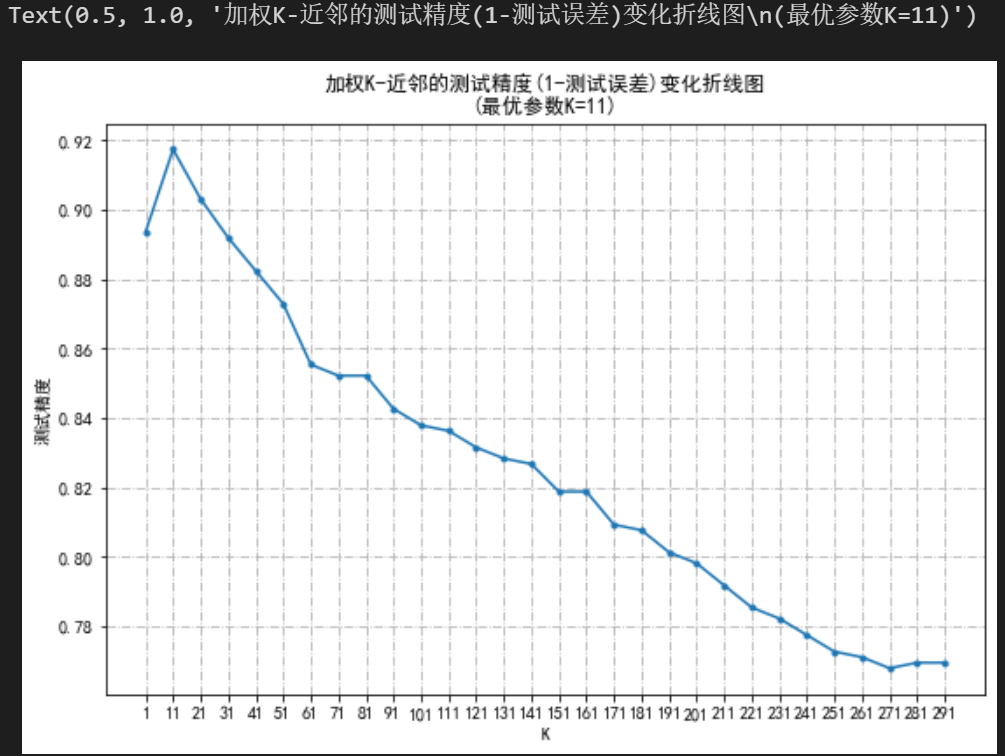
最优参数K为11,选择该参数下的K-近邻法进行分类预测,
modelKNN=neighbors.KNeighborsClassifier(n_neighbors=bestK,weights='distance')
modelKNN.fit(X_train,Y_train)
#通过classification_report计算模型在整个数据集的预测精度
print('评价模型结果:\n',classification_report(Y,modelKNN.predict(X)))输出:
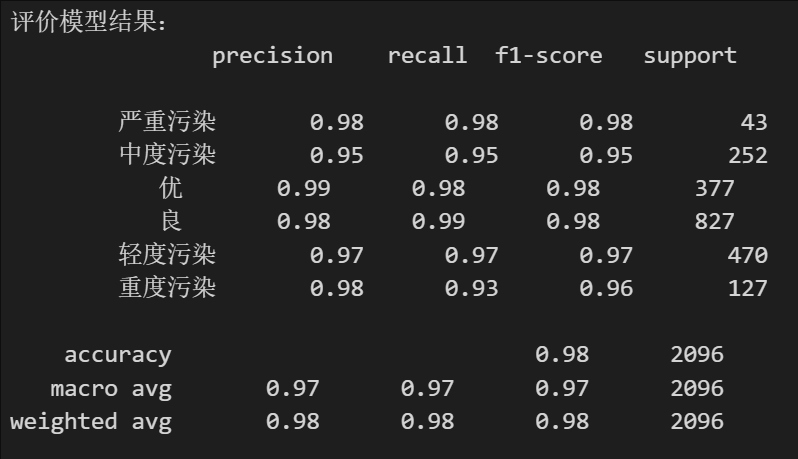
可以看到,模型在中度污染的预测中,查准率P、查全率R和F1分数均等于0.95。对重度污染预测中,模型的查准率P较高而查全率R略低。
(四)K-近邻法做回归预测
下面示例通过K-近邻法做电视剧的大众评分预测:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import sklearn.linear_model as LM
from sklearn.metrics import classification_report
from sklearn.model_selection import cross_validate,train_test_split
from sklearn import neighbors,preprocessing
data=pd.read_excel('电视剧播放数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
data=data.loc[(data['点赞']<=2000000) & (data['差评']<=2000000)]
data.head()输出:
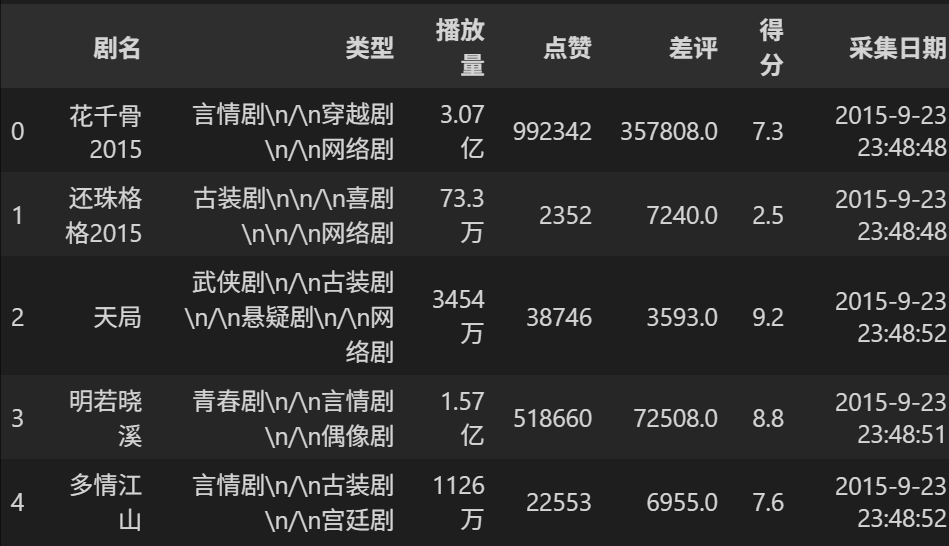
X=data.loc[:,['点赞','差评']]
Y=data.loc[:,'得分']
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.70, random_state=123)
#采用20-近邻法
modelKNN=neighbors.KNeighborsRegressor(n_neighbors=20)
modelKNN.fit(X_train,Y_train)
print('K-近邻:测试精度=%f总预测精度=%f'%(modelKNN.score(X_test,Y_test),modelKNN.score(X,Y)))
#建立线性回归模型
modelLR=LM.LinearRegression()
modelLR.fit(X_train,Y_train)
print('一般线性回归模型:测试精度=%f;总预测精度=%f'%(modelLR.score(X_test,Y_test),modelLR.score(X,Y)))输出:
![]()
20-近邻法和线性回归模型的预测性能对比:
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(12,4))
axes[0].scatter(X.iloc[:,0],Y,s=2,c='r')
index = np.argsort(X.iloc[:,0])
axes[0].plot(X.iloc[index,0],modelKNN.predict(X.iloc[index,:]),linewidth=0.5,label="K-近邻")
axes[0].plot(X.iloc[index,0],modelLR.predict(X.iloc[index,:]),linestyle='--',linewidth=1,label="一般线性回归模型")
axes[0].set_title('点赞数和得分',fontsize=12)
axes[0].set_xlabel('点赞数',fontsize=12)
axes[0].set_ylabel('得分',fontsize=12)
axes[0].legend()
#仅展示了点赞数低于25万电视剧的点赞数和得分预测值的情况
data=data.loc[(data['点赞']<=250000)]
axes[1].scatter(data['点赞'],data['得分'],s=2,c='r')
T=X.loc[(X['点赞']<=250000)]
index = np.argsort(T.iloc[:,0])
axes[1].plot(T.iloc[index,0],modelKNN.predict(T.iloc[index,:]),linewidth=0.5,label="K-近邻")
axes[1].plot(T.iloc[index,0],modelLR.predict(T.iloc[index,:]),linestyle='--',linewidth=1,label="一般线性回归模型")
axes[1].set_title('点赞数和得分',fontsize=12)
axes[1].set_xlabel('点赞数',fontsize=12)
axes[1].set_ylabel('得分',fontsize=12)
axes[1].legend()输出:
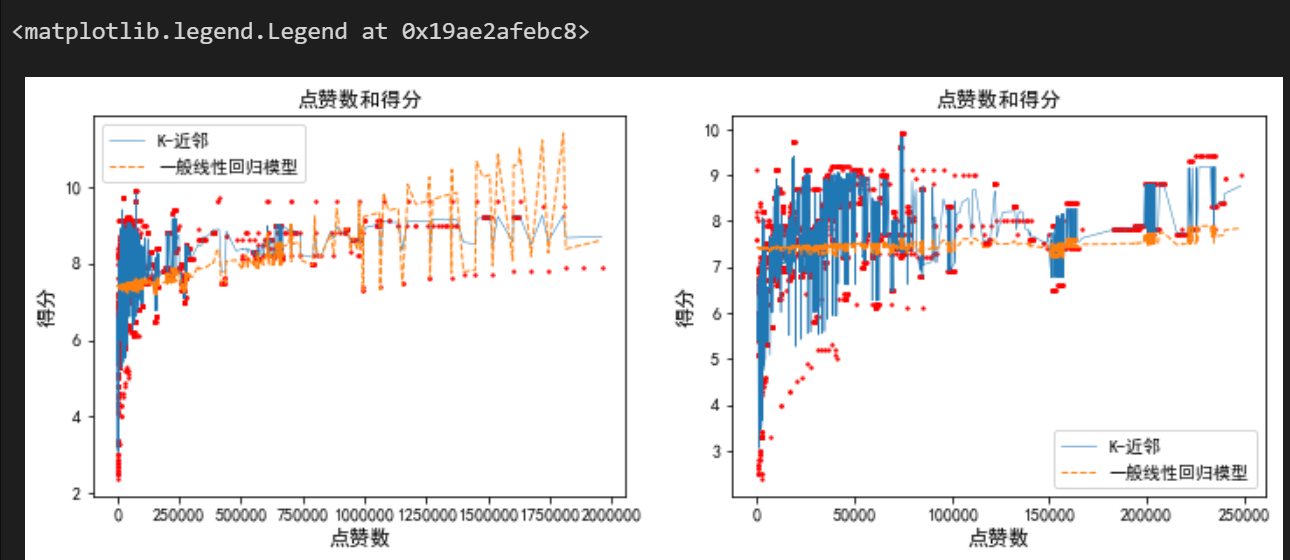
左图中,实线对应 20-近邻法的预测结果,虚线对应一般线性回归模型的预测结果。整体上似乎并没有一般线性回归模型不理想的明显特点,且在图形的右侧区域一般线性回归模型对点的拟合还优于20-近邻法。那么为什么一般线性回归模型的
很低呢?(
越接近 1 拟合越好,低说明模型解释力弱)原因在于得分和点赞数之间并没有显著的线性关系。
左图显示大部分电视剧的点赞数低于25 万。为此,右图仅展示了点赞数低于 25万电视剧的点赞数和得分预测值的情况。可见,20-近邻法对这部分数据点的拟合明显好于一般线性回归模型,且整体上得分和点赞数之间并不存在显著的线性关系。
资料百度网盘自取:
链接: https://pan.baidu.com/s/1TmmBgk7-3hs6qipAJny2Ug?pwd=2jsq 提取码: 2jsq






















 3981
3981

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








