达摩院 ICLR‘25 Spotlight | MaRS：自带条件输入的扩散模型如何快速采样？

摘要

在扩散模型的应用中，可控生成具有重要的实际价值，但也具有挑战性。目前的可控生成方法主要聚焦于扩散模型的得分函数（score function）或神经网络结构，而均值回归扩散模型（Mean Reverting Diffusion, MR Diffusion）直接修改随机微分方程（SDE）的结构，使图像控制条件的引入更加简单自然，在图像超分、修复、增强等图生图任务中极具应用价值。然而，当前无需训练的快速采样器无法用于MR Diffusion。 因此，本文提出了一种适用于 MRD 的快速采样算法——MR Sampler（MaRS）。该算法通过求解 MRD 对应的逆时 SDE 和概率流常微分方程（PF-ODE）得到半解析解，其中的解析部分可以精确计算。基于此解决方案，我们可以用更少的NFE（Number of Function Evaluation）生成高质量的样本。该算法无需训练，并支持所有主流的参数化方式。 实验表明，MR Sampler可以在10种不同的图像恢复任务中保持较高的采样质量，并且能将采样速度提高10 ~ 20倍。 Arxiv: https://arxiv.org/abs/2502.07856 Github: https://github.com/grrrute/mr-sampler.git

背景知识

扩散概率模型（Diffusion Probabilistic Model, DPM）可以通过一对随机微分方程定义：

 

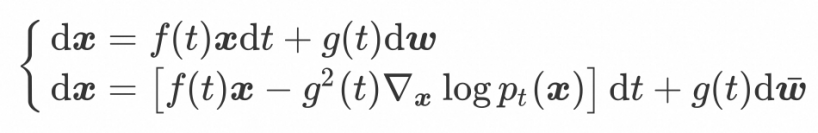
方程 1 描述前向过程：向数据中加入噪声，直至变为纯高斯噪声。

方程 2 描述对应的逆向过程：从纯粹的高斯噪声中逐渐移除噪声并恢复原始数据。

常用的扩散模型都可以被统一为 DPM 的形式，包括Variance Preserving-SDE（DDPM）和Variance Exploding-SDE（NCSN，EDM等），如下表所示：

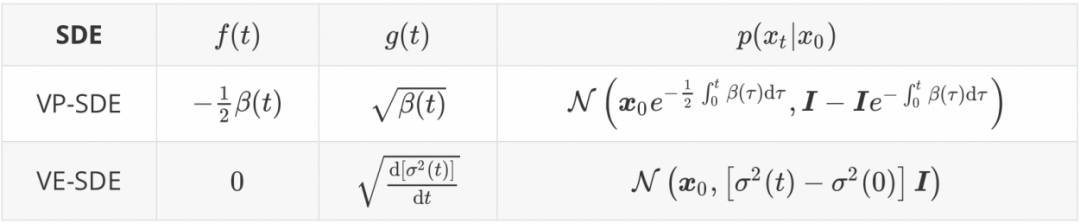
均值回归扩散模型（Mean Reverting Diffusion）提出一类特殊的 SDE 结构：

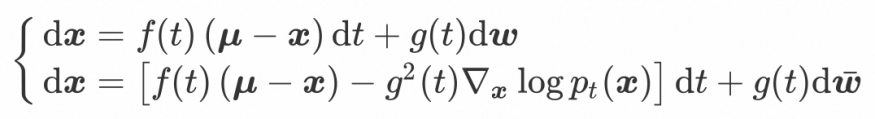
状态均值的引入改变了前向过程的结果，使其最终状态服从一个非零均值的高斯分布，这为引入图像条件提供了一种简单自然的方式。这种特性使 MR Diffusion 特别适合解决逆问题，并可能扩展到多模态条件。

针对噪声参数化的快速采样算法

扩散模型的训练来自得分匹配（score matching）方法，后面被简化为不同的参数化预测，其中最常用的是噪声预测，其逆向过程对应的SDE为：

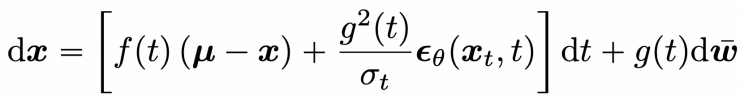
利用微分形式的伊藤公式，可以得到一个半解析解。

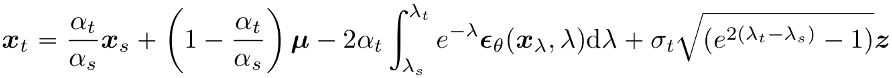
其中，

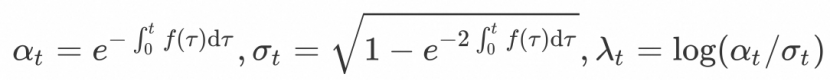
此外，扩散模型的采样还可以通过概率流常微分方程（PF-ODE）计算，如下所示：

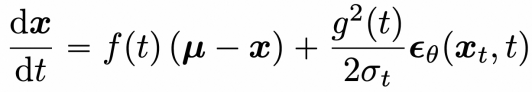
利用“常数变易法”，可得：

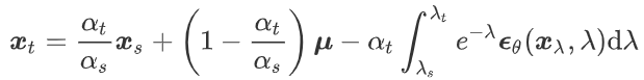
上述两个解的积分项包含神经网络输出，无法精确计算，通过名为“数值积分器”的数值估计方法近似计算。

针对数据参数化的快速采样算法

基于噪声参数化的方法具有较为简单的形式，然而数值稳定性不佳，在NFE低于20的情况下采样质量显著下滑。相比之下，基于数据参数化的预测具有较好的数值稳定性，具体分析请参考实验部分。数据参数化对应的逆时SDE和PF-ODE具有更为复杂的结构，如下所示：

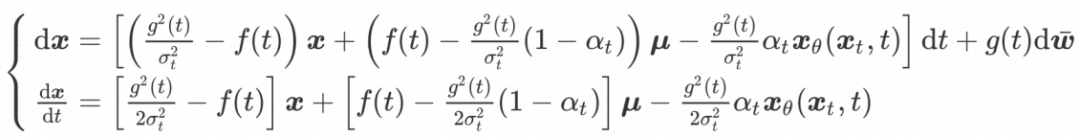
利用上一节中类似的方法，可得相应的解。

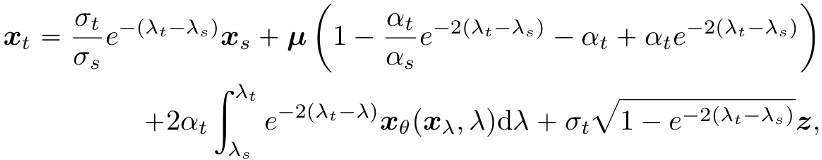
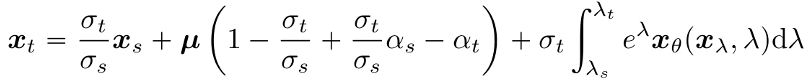
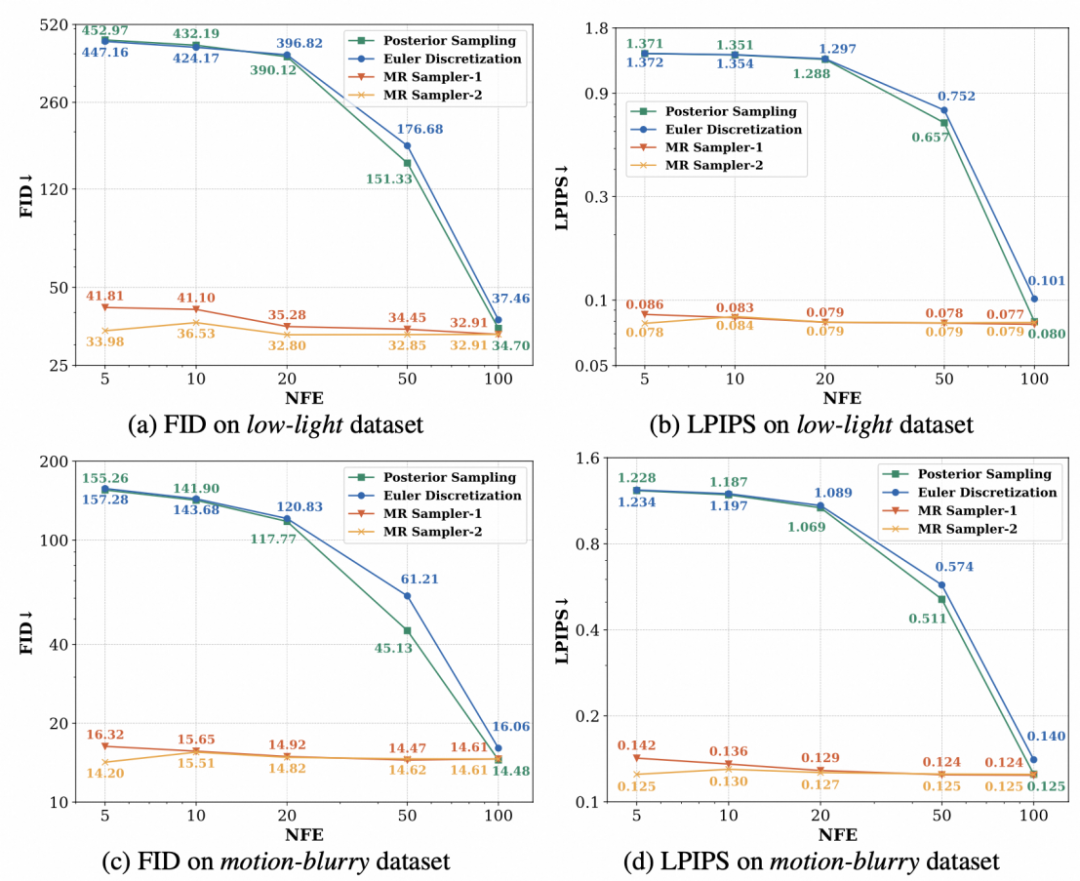
实验

我们在 10 种图像复原任务上进行了实验，结果表明，MR Sampler在 10-20 倍加速采样的情况下保持较高的质量（这里展示两个数据集的结果，完整实验结果请参考原文附录）。

采样轨迹

扩散模型在采样时需要对图像进行迭代，如果将每一步的中间状态视作高维空间中的一个点，将这些点按照采样顺序连接起来，就能得到一条采样轨迹，这有助于我们对采样过程有一个直观的认识。高维空间难以观测，但可以利用PCA（Principal Component Analysis）将所有点降至二维空间。

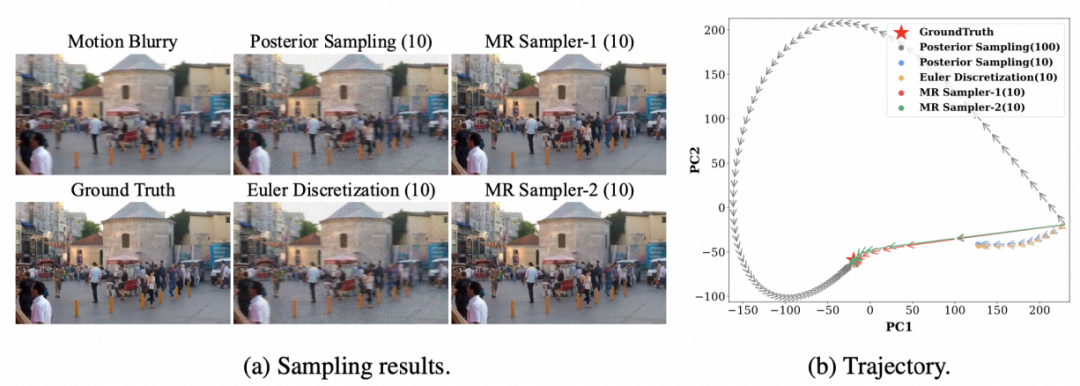
这里选择“去运动模糊”任务中的数据为例，图 a 展示了原图、GroundTruth以及各类方法的结果；图 b 展示了每种方法对应的采样轨迹。

可以看出，MR Sampler由于每一步的误差小，能够以较少的步数抵达正确的“终点”。

数值稳定性分析

前面提到，基于噪声的参数化在NFE低于 20 的情况下效果不佳。我们分析了采样算法的误差来源，认为关键在于对积分项的数值估计。我们使用“指数积分”方法估计解的积分项，其中包含对神经网络函数的 Taylor 展开，而Taylor展开存在收敛域的限制，要满足以下要求：

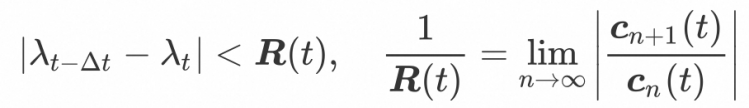
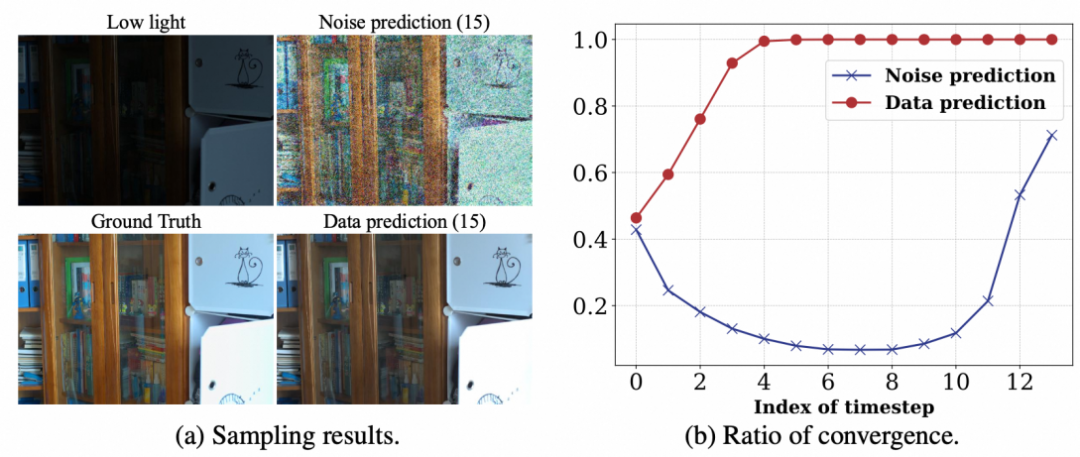
其中 c 对应神经网络函数关于信噪比 lambda 的 n 阶导数。由于神经网络输出是一个张量，因此连带收敛域也是张量，我们统计了每一步采样中符合收敛域的分量比例，如下图所示。可以看出，基于数据参数化的算法在采样几步后可以快速收敛。

直观来看，数值估计方法是选取有限个点去近似函数的一段积分，噪声参数化的神经网络预测的是相邻步状态的差分，其函数数值变化剧烈；而数据参数化的神经网络预测的是“干净图像”，每一步的预测结果相差不大，函数数值较为稳定。因此，基于数据参数化的算法具有更高的实际价值。

总结

我们提出了一种适用于 Mean Reverting Diffusion 的快速采样算法，无需额外训练且支持多种参数化训练目标。我们通过求解相应的逆时 SDE 和 PF-ODE，得到具有半解析结构的解，并利用“指数积分”法估计非解析项的积分。我们还提供了可视化的采样轨迹，并尝试分析了数值稳定性的来源以及数据参数化更稳定的原因。

实验结果证明该算法能够在 10-20 倍加速的情况下保持采样效果，为 MR Diffusion 在实际场景下的应用奠定了基础，未来我们将探索基于 MR Diffusion 的 LDM 在医学影像增强、噪声抑制和超分辨率等任务上的潜力与价值。