整数和浮点数在内存中存储

整数的存储:

存储形式:

整数的存储是以二进制来存储，例如存储a=5转换成二进制形式为:101.

常见平台二进制位数有64位和32位，顾名思义,需要64位或者32位二进制来存储一个整数.

所以上述存储a=5时，在32位平台的实际存储为:00000000000000000000000000000101.

高位不够补0即可。64位平台同理，补够二进制位数即可。

在计算机中整形的存储实际是按补码形式存储，调用时在转化为源码使用(此处补码就不再赘叙),

补码原码的转换如下:a=5实际存储的是补码，但正数的原反补相同。

大大小端存储:

大小端字节序指的是在多字节数据类型的存储过程中，字节的排列顺序。

一位十六进制可以用4位二进制来表示，所以32位二进制位可以用8位16进制来表示.

例如:a=5;在32位平台的实际存储为:00000000000000000000000000000101.

用十六进制表示:0x00 00 00 0b.但此时又涉及到存储顺序的问题，为了方便取值可以从左到右存储，当然也可以从左到右存储。

大端字节序:数值的低位字节序放到高位地址中

如图:所以当大端存储时存储的值是 0x0b 00 00 00

小端字节序:数值的低位字节序放到低位地址中

如图:所以当小端存储时存储的值是 0x00 00 00 0b

目前多数编译器采用的是小端存储:

在内存窗口输入&a，此时a的存储就是小端存储.(注:内存块以二进制存储，在内存窗口上以十六进制展示,故此时是以十六进制表示)

判断当前整形存储形式是大端还是小端:

采用变量a来测试

为了判断存储形式，可以将第一个字节取出，看这个值为多少:

若值为 0，则是大端存储，反而就是小端存储。代码实现如下:

#include<stdio.h>

int judge(int *i)
{
	if (*(char*)i == 1)
	return 1;//小端
	else
	return 0;//大端
	//数据转化截断从低地址开始
}

int main()
{
	int a = 1;
	// 0x 00 00 00 01
	//大端: (低地址) 00 00 00 01 (高地址)
	//小端: (高地址) 01 00 00 00 (低地址)

	//取出第一个字节判断即可

	if (judge(&a) == 1)
		printf("小端存储!");
	else
		printf("大端存储!");

	return 0;
}

浮点数在内存中存储:

存储形式:

浮点数与整形数存储不同，浮点型的存储只用存储三个数即可。

针对浮点数(即小数)可以用科学计数法来表示:如 0.5 可以表示为 5*10^(-1)

已知计算机上的存储形式为二进制所以只要将其以二进制位的科学计数法表示即可。

遵循标准：V = (-1)^s  * 2^E * M

// (-1)^s 符号位,s为0,V是正数.s为1，V是负数
//   2^E  指数位
//    M   有效数字,M是大于等于1,小于等于2

例如: 5.5 的二进制位为: 101.1，实际存储就是  (-1)^0 * 1.011 * 2^2

不同平台下的 S、E、M 所占字节大小

// 32位平台 :   S - 1bit   E - 8bit    M - 23bit
// 64位平台 :   S - 1bit   E - 11bit   M - 52bit

注意:

M的值表示精度，为了提升精度要对M做一些处理

M的存储:由于M总是>1，所以可以舍弃第一位的1，只存取小数点后的位
例如存储1.01只保存01，最后读取时再加上第一位的1。

当数值过小,指数位E的值可能小于0，

E的存储:由于E可能为负数，所以存储必须加一个中间值，调用时再减去中间值
float(E=8bit):中间值=127。 double(E=11bit):中间值=1023。
如: 2^10 ,E等于 10，但存储时 E = 10+127 =137(10001001);

特殊:

1.E不为全0或者全1

正常:指数E的计算值减去中间值,得到真实值->有效数字M加上第一位的1

2.E为全0

数值无穷接近于0，指数E的真实值 等于 1减去中间值 ->有效数字M不在加上第一位的1

3.E全为1

数值表示正负无穷大,有效数字M全为0，不加以讨论

例题:

例1:

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>

int main()
{
	int n = 9;//整数的存储:补码
	// 00000000 00000000 00000000 00001001
	float* pfloat = (float*)&n;
	// 0 00000000 00000000000000000001001
	// S    E               M
	//E为全0,E的真实值为 -126
	// (-1)^0 * 0.00000000000000000001001 * 2^(-126)
	// 0.000000
	printf("n的值是: %d\n", n);//9
	printf("*pfloat的值是: %f\n", *pfloat);//0.000000

	return 0;
}

结果:

例2:

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>

int main()
{
	int n = 9;//整数的存储:补码
	// 00000000 00000000 00000000 00001001
	float* pfloat = (float*)&n;

	*pfloat = 9.0;
	// (-1)^0 * 1.001 * 2^3
	//  S=0    M=1.001  E=3
	//  s=0    E=130    M=001
	//   0     10000010 00100000000000000000000(实际存储)

	printf("n的值是: %d\n", n);//1091567616
	printf("*pfloat的值是: %f\n", *pfloat);//9.000000

	return 0;
}

结果:

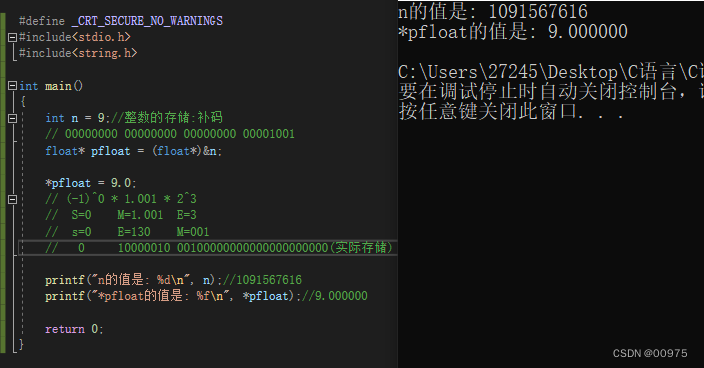
这两个例题嘎嘎重要，相关注释已经标注上去，如有疑问可以关注私信我哟！

都看到这里了，给个赞可以吗