P8866 [NOIP2022] 喵了个喵

最新推荐文章于 2024-10-04 21:14:49 发布

AC_Hunter_LC

最新推荐文章于 2024-10-04 21:14:49 发布

阅读量684

点赞数 9

文章标签：算法 c++ 数据结构

本文链接：https://blog.youkuaiyun.com/weixin_64565306/article/details/141640801

版权

题目描述

小 E 喜欢上了一款叫做《喵了个喵》的游戏。这个游戏有一个牌堆和 nn 个可以从栈底删除元素的栈，任务是要通过游戏规则将所有的卡牌消去。开始时牌堆中有 mm 张卡牌，从上到下的图案分别是 a1,a2,…,ama1,a2,…,am。所有的卡牌一共有 kk 种图案，从 11 到 kk 编号。牌堆中每一种图案的卡牌都有偶数张。开始时所有的栈都是空的。这个游戏有两种操作：

选择一个栈，将牌堆顶上的卡牌放入栈的顶部。如果这么操作后，这个栈最上方的两张牌有相同的图案，则会自动将这两张牌消去。
选择两个不同的栈，如果这两个栈栈底的卡牌有相同的图案，则可以将这两张牌消去，原来在栈底上方的卡牌会成为新的栈底。如果不同，则什么也不会做。

这个游戏一共有 TT 关，小 E 一直无法通关。请你帮小 E 设计一下游戏方案，即对于游戏的每一关，给出相应的操作序列使得小 E 可以把所有的卡牌消去。

输入格式

第一行包含一个正整数 TT，表示数据组数。

接下来一共 TT 组数据，在每组数据中：

第一行包含三个正整数 n,m,kn,m,k，分别表示栈的个数、卡牌的个数、卡牌上图案的种类。

第二行包含 mm 个正整数，分别表示 a1,a2,…,ama1,a2,…,am，分别从上到下表示牌堆中卡牌的图案。

输入数据保证有解。

输出格式

对于每一组数据，输出若干行。

其中第一行包含一个正整数 opop，表示操作的次数。你需要保证 m≤op≤2×mm≤op≤2×m。

接下来 opop 行，每行包含两个或三个正整数，整数之间用一个空格隔开。

若为两个整数 1 s1 s，则进行一次第一个操作并选择栈 ss。

若为三个整数 2 s1 s22 s1 s2，则进行一次第二个操作并选择栈 s1s1 和 s2s2。

你需要保证 1≤s,s1,s2≤n1≤s,s1,s2≤n，且 s1≠s2s1=s2。

输入输出样例

输入 #1

1
2 4 2
1 2 1 2

输出 #1

说明/提示

【样例 1 解释】

下图是初始状态。

下图是前两次操作之后的结果。

下图是第三次和第四次操作之后的结果。

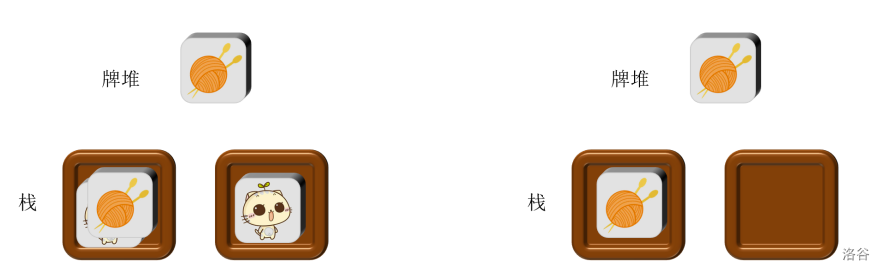
下图是第五次操作之后的结果。

【样例 2】

见选手目录下的 meow/meow2.inmeow/meow2.in 与 meow/meow2.ansmeow/meow2.ans。

【数据范围】

设 SS 为所有 TT 组数据中 mm 的总和。

对于所有数据，保证 S≤2×106S≤2×106，1≤n≤3001≤n≤300，1≤ai≤k1≤ai≤k。

测试点	T=T=	nn	k=k=	m≤m≤
1∼31∼3	10011001	≤300≤300	2n−22n−2	无限制
4∼64∼6	10021002	=2=2	2n−12n−1	无限制
7∼107∼10	33	=3=3	2n−12n−1	1414
11∼1411∼14	10041004	=3=3	2n−12n−1	无限制
15∼2015∼20	10051005	≤300≤300	2n−12n−1	无限制

【评分方式】

对于每一组数据，若在按顺序进行所有操作后，牌堆为空且所有的栈均为空，则认为你的答案正确。

【提示】

你可以通过 TT 的个位数来判断这个测试点是属于哪一类数据。

你的输出不需要与样例输出一致，输出任意一个合法解即可得分。

附件下载

meow.zip 192.65KB

思路

假定当前牌堆顶的牌的种类为 xx，现在场上也有至少一张种类为 xx 的牌，然后我们想把这张牌直接消掉。

在以下的策略中如果场上有两张相同的牌，我们一定会立刻将它们消掉，所以同种类的牌于此条件下在场上只能出现一次。假定场上另一张种类为 xx 的牌位于栈 pxpx 中。

如果 pxpx 的顶端卡牌种类为 xx，则将当前牌堆顶的牌放到栈 pxpx 上，它们会自动被消掉。
如果 pxpx 的底端卡牌种类为 xx，则将当前牌堆顶的牌放到一个空栈 spsp 上，然后对栈 spsp 和 pxpx 执行一次操作二，它们也会被消掉。

（以下同颜色代表同种类的牌）

第一种操作示例：

操作1

第二种操作示例：

操作2

不难发现如果一个栈里有不少于三张牌的话，那么位于中间的那一张是不容易被消掉的，而 kk 的范围在 2n2n 左右，这启发我们尽可能使每个栈含有不超过两张牌。

k=2n−2k=2n−2

策略1：存在一个编号为 spsp 的空栈，且当前牌堆顶的牌在场上存在或其余栈中存在至少一个栈大小不超过 11：

如果当前牌堆顶的牌在场上出现过，按上述消除基本策略执行（将栈 spsp 第二种消除操作的空栈）。
否则将其放到任意一个其中大小不超过 11 的栈的栈顶 （spsp 号栈除外）。

由于只有 k=2n−2k=2n−2 种卡牌，我们可以保证即使前 n−1n−1 个栈均含有两张卡牌时，牌堆顶的牌也一定会在场上出现过，可以重复按照策略1执行。令 nn 号栈为 spsp 空栈，便可保证第二种消除基本策略的执行。

k=2n−1k=2n−1

现在多了一种牌，所以策略1不一定每次都能奏效了。

那么考虑如何安置多出来的这一种牌。我们再看牌堆顶的下一张牌，如果这张牌的同类牌出现在栈底（不妨设对应栈编号为 pp），那么不难得出可以将牌堆顶的牌放到栈 pp 上，然后将下一张牌放到栈 spsp 里，最后对栈 pp 和 spsp 执行一次操作2便可安置。

但是如果下一张牌的同类牌在栈顶的话，我们可以无脑将牌堆顶的牌放到栈 spsp 上吗？显然不可以：

既然消除的关键还是栈底的牌，所以我们可不可以拓宽一下视野，往后看有没有位于底部的牌，然后将牌堆顶的牌放到对应栈顶呢？

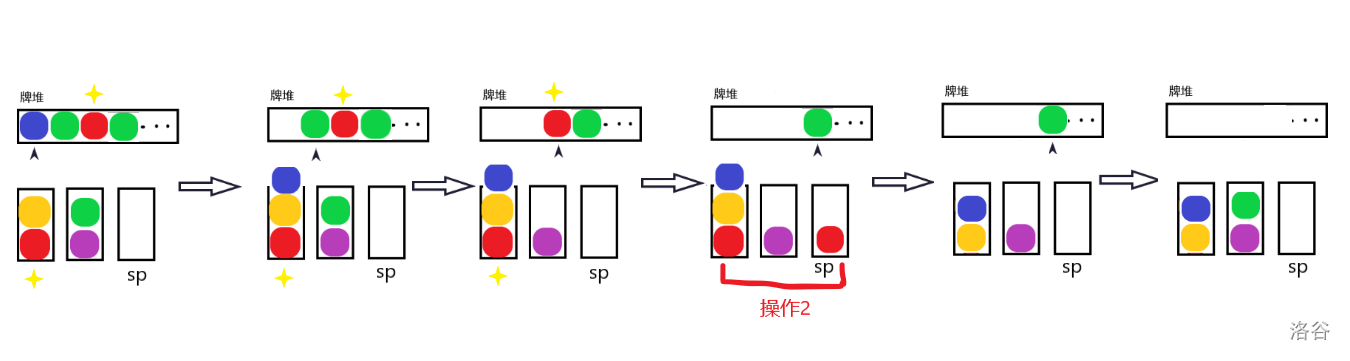
貌似很行，对吧。

还是不行。牌堆顶的牌阻挡了原栈顶的牌，使得它们不能互相消除。

但如果我们改为将牌堆顶的牌放到 spsp 里....

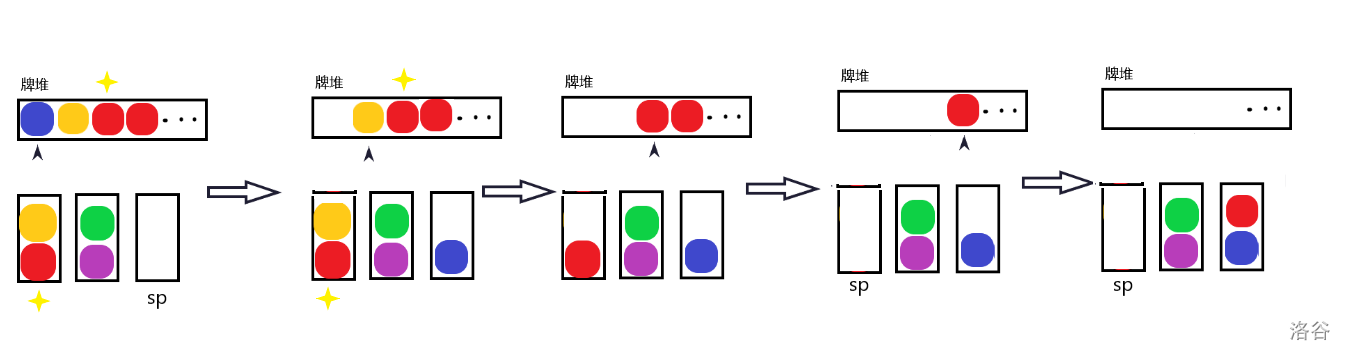
这样反而行得通了，唯一的区别就是 spsp 换了一下。

那么两者的区别是什么呢？仔细观察就可以发现：

前者第一张位于底部的牌所在栈的栈顶牌没有被消去，后者被消去了。

什么情况下栈顶元素会被消去？结合上述图思考一下便可得知：

在牌堆顶和其后第一张位于栈底的牌之间，与栈顶牌同类的牌出现了奇数次。

至于这两张牌之间的所有牌，由于它们都出现在栈顶出现，所以直接将其分别放在对应栈上即可。（当然一些牌会出现多次，在这种情况下为了方便，可以每次都将其放在同样的位置。）

于是策略便逐渐明朗起来：

策略 Meow：存在一个编号为 spsp 的空栈，且不满足策略1条件。

首先记录此时每类牌所在的栈编号和是否位于栈顶，记 pipi 此时牌 ii 同类的牌所位于的栈编号，ti=1ti=1 代表此时牌 ii 同类的牌位于栈顶。

然后从牌堆顶的下一张开始，逐个向后判断。设当前判断的牌为 xx。

若 tx=1tx=1，则将 xx 放到栈 pxpx 的栈顶，然后判断下一张。
否则若 xx 与牌堆顶的牌同类，将这两张牌放到 spsp 里，然后更换使用策略1或重新使用策略 Meow。
否则：
- 若与栈 pxpx 的栈顶牌同类的牌在牌堆顶至 xx 这些牌之间出现了奇数次，则将此时牌堆顶的牌放置于栈 spsp，将 xx 放置于栈 pxpx，然后将 spsp 改为 pxpx。
- 若与栈 pxpx 的栈顶牌同类的牌在牌堆顶至 xx 这些牌之间出现了偶数次，则将此时牌堆顶的牌放置于栈 pxpx，将 xx 放置于栈 spsp，然后在栈 spsp 和 pxpx 上执行一次操作 22。
  
  执行以上两种操作之一后更换使用策略1或重新使用策略 Meow 即可。

当然，由于将牌加入至栈的过程是有序的，所以在实现上会有些许不同。（例如，可以先找到 xx 在哪里，然后根据信息判断牌堆顶的牌应放置在哪里，最后将牌堆顶之后的牌加入栈。）

重复执行策略1和策略 Meow，最终所有的牌均可以被消掉。这样我们也可以证明所有合法的初始配置均有解。

整体操作示例

对于操作次数：我们会执行恰好 mm 次操作1，而每次操作2会消除两张牌，由于操作1执行过程中也会消去牌，因此 2m2m 张牌至多使用 mm 次操作2即可全部消除，于是总操作次数不超过 m+m=2mm+m=2m，符合条件。

数据范围较大（∑m≤2×106∑m≤2×106），所以需要注意复杂度和常数。

代码

#include<bits/stdc++.h>
using namespace std;
//AC_Hunter
int a[2000005],p[1000],b[1005];
deque<int>q[1000];
vector<pair<int,int>>ans;
int pos=1,sz;
int cnt[1005];
queue<int>pq0;
void change(int x,int y){
	ans.push_back({x,y});
	if(y==0){
		pq0.push(x);
		if(!q[x].empty() and q[x].back()==a[pos]){
			q[x].pop_back();
			cnt[a[pos]]--;
			if(cnt[a[pos]]==0)sz--,p[a[pos]]=0;
			if(q[x].empty())b[a[pos]]=0;
		}
		else{
			q[x].push_back(a[pos]);
			if(cnt[a[pos]]==0){
				sz++,p[a[pos]]=x;
			}
			cnt[a[pos]]++;
			if(q[x].size()==1)b[a[pos]]=1;
		}
		pos++;
	}
	else{
		pq0.push(x);
		pq0.push(y);
		if(q[x].front()==q[y].front()){
			b[q[x].front()]=0;
			cnt[q[x].front()]-=2;
			if(cnt[q[x].front()]==0){
				sz--,p[q[x].front()]=0;
				b[q[x].front()]=0;
			}
			q[x].pop_front();
			q[y].pop_front();
			
			if(!q[x].empty())b[q[x].front()]=1;
			if(!q[y].empty())b[q[y].front()]=1;
		}
	}
}
int main(){
	int t;
	cin>>t;
	while(t--){
		pos=1;
		sz=0;
		memset(p,0,sizeof p);
		memset(b,0,sizeof b);
		ans.resize(0);
		int n,m,k;
		cin>>n>>m>>k;
		int sp=n;	
		while(!pq0.empty())pq0.pop();
		for(int i=1;i<=n;i++){
			if(i!=sp)pq0.push(i);
		}
		int ap[k+5]={0};
		for(int i=1;i<=m;i++){
			cin>>a[i];
			a[i+1]=0;
		}
		for(int i=1;i<=m;i++){
			if(sz==2*(n-1) and !cnt[a[i]]){
				int ti=i;
				for(int j=i+1;j<=m;j++){
					if(a[j]==a[i]){
						for(int w=i+1;w<=j;w++){
							ap[a[w]]=p[a[w]];
						}
						change(sp,0);
							for(int w=i+1;w<=j;w++){
								if(a[w]==a[i])change(sp,0);
								else change(ap[a[w]],0);
							}	
						i=j;
						break;
					}
					if(b[a[j]]){
						if(ap[q[p[a[j]]].back()]){
							for(int w=i+1;w<=j;w++){
								ap[a[w]]=p[a[w]];
							}
							change(sp,0);
							sp=p[a[j]];
							for(int w=i+1;w<=j;w++){
								change(ap[a[w]],0);
							}	
						}
						else{
							for(int w=i+1;w<=j;w++){
								ap[a[w]]=p[a[w]];
							}
							change(p[a[j]],0);
							for(int w=i+1;w<j;w++){
								change(ap[a[w]],0);
							}
							change(sp,0);
							change(sp,p[a[j]]);
						}
						i=j;
						break;
					}
					else{
						ap[a[j]]^=1;
					}
				}
				for(int j=ti;j<=i;j++){
					ap[a[j]]=0;
				}
				continue;
			}
			if(p[a[i]]){
				if(q[p[a[i]]].back()==a[i]){
					change(p[a[i]],0);
				}
				else{
					change(sp,0);
					change(sp,p[a[i]]);
				}
			}
			else{
				while(!pq0.empty() and (pq0.front()==sp or q[pq0.front()].size()>=2)){
					pq0.pop();
				}
				change(pq0.front(),0);
			}
		}
		cout<<ans.size()<<endl;
		for(auto it:ans){
			if(it.second==0)cout<<1<<' '<<it.first<<'\n';
			else cout<<2<<' '<<it.first<<" "<<it.second<<'\n';
		}
		assert(pos==m+1);
		for(int i=1;i<=n;i++){
			assert(q[i].empty());
		}
	}
	return 0;
}