05 mobilenet系列（1、2、3）

  

仅是个人笔记，代码学习资源来源B站博主霹雳吧啦Wz的个人空间_哔哩哔哩_bilibili

一、 理论知识

1. MobileNet（2017）

专注于移动端或者嵌入 式设备中的轻量级CNN网络；

在准确率小幅降低的前提下大大减少模型参数与运算量。

1.1 Depthwise Convolution

大大减少运算量和参数数量

传统卷积： 卷积核channel=输入特征矩阵channel；输出特征矩阵channel=卷积核个数

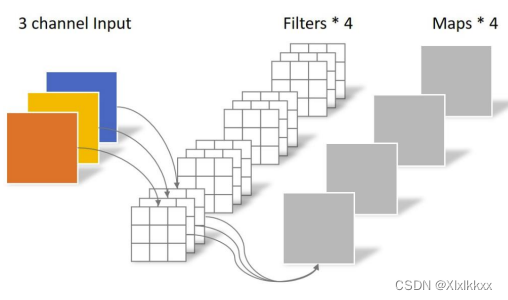
DW卷积： 卷积核channel=1； 输入特征矩阵channel=卷积核个数=输出特 征矩阵channe

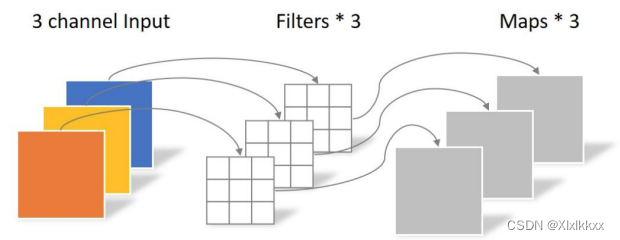
1.2 Pointwise Convolution

 PW卷积运算与常规卷积运算非常相似，它的卷积核的尺寸为 1×1×M，M为上一层的通道数。PW卷积运算会将上一步的map在深度方向上进行加权组合，生成新的Feature map。有几个卷积核就有几个输出Feature map。

2. MobileNet V2（2018）

准确率更高，模型更小

2.1 倒残差结构

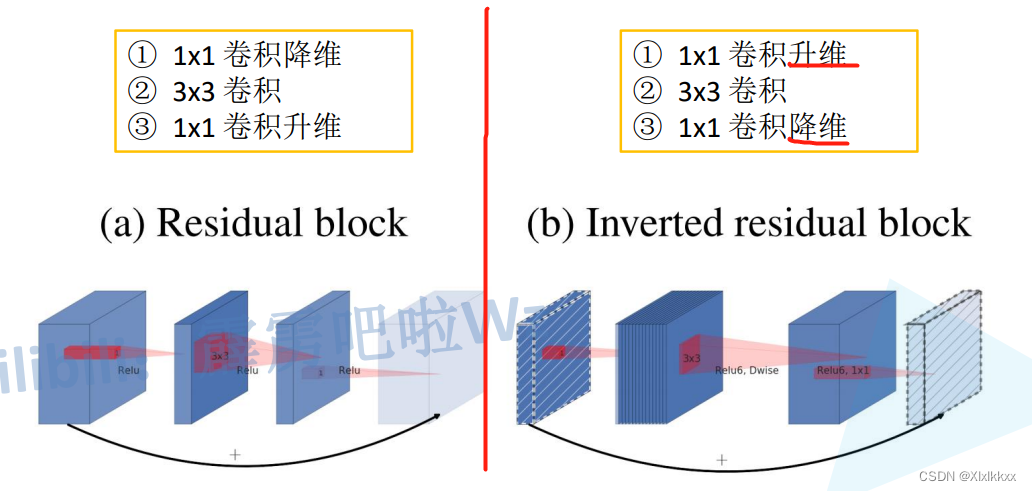
使用两种block

•  当stride=1且输入特征矩阵与输出特征矩阵shape相同时才有shortcut连接
•  激活函数：y  =  ReLU6(x)  = min(max(x, 0), 6）
•  普通卷积和DW卷积都有用到
•  具体实现看代码，不过于纠结结构图

2.2 MobileNet V2参数配置表

参数说明：

t是扩展因子（block中间卷积过程输入输出通道的倍数关系）----结合下图看就懂了

c是输出特征矩阵深度channel

n是bottleneck的重复次数

s是步距（针对第一层，其他为1）

 每个block内部的输入输出特征图变化

3. MobileNet V3（2019）

更准确，更高效

3.1 更新V2的block

具体改进看下图对比：

 上图中第3个特征图——第四个特征图如何变换的------通过SE

3.2 加入SE模块

加入SE模块也就是上图中的绿色圈圈

SE具体操作见下图：

3.3 设计激活函数

3.4 参数表

MobileNetV3-Large、MobileNetV3-Small

一般用不到自己搭建，随看随搜

二、 代码复现

1. DW卷积

nn.Conv2d(in_channel, out_channel, kernel_size, stride, padding, groups=groups, bias=False)
#  参数groups决定
#  groups为1是就是普通卷积， groups=in_channel=out_channel时为DW卷积

2. SE代码实现：

# 02 求 "注意力"小棒子操作
class SqueezeExcitation(nn.Module):
    def __init__(self, input_c: int, squeeze_factor: int = 4):
        super(SqueezeExcitation, self).__init__()
        squeeze_c = _make_divisible(input_c // squeeze_factor, 8)
        self.fc1 = nn.Conv2d(input_c, squeeze_c, 1)
        self.fc2 = nn.Conv2d(squeeze_c, input_c, 1)

    def forward(self, x: Tensor) -> Tensor:                     #举例说明：输入8，4，4----输出8，4，4   参数设置：input_c=8， squeeze_c=16
        scale = F.adaptive_avg_pool2d(x, output_size=(1, 1))             #scale的变化如下   8，4，4----8，1，1
        # 自适应池化可改变特征图大小， (1, 1)代表池化后结果为1*1特征图
        scale = self.fc1(scale)                                          #                8，1，1----16，1，1
        scale = F.relu(scale, inplace=True)
        scale = self.fc2(scale)                                          #                16，1，1----8，1，1
        scale = F.hardsigmoid(scale, inplace=True)
        return scale * x          # scale就是系数，shape8，1，1   与输入x,shape8，4，4 相乘     得到最终的输出8，4，4

3. tensor乘法

•    *      等价于    torch.mul 

元素一一相乘：

情况一：

A B  shape完全相同，对应位置元素相乘

情况二：

A B  shape不同也可相乘，会自动复制成相同shape再对应相乘： 

torch.tensor([1, 2, 3]) * 2 = torch.tensor([2, 4, 6]) 

# 先将2复制为[2,2,2]   [1, 2, 3]*[2,2,2]=[2, 4, 6]


# 再比如上面的SE操作的最后一步，同样道理
（8，4，4）*（8，1，1）  

•  torch.matmul

1. 向量点乘

x = torch.tensor([1, 2, 3])
y = torch.tensor([4, 5, 6])
torch.matmul(x, y)

# tensor(32)

2. 二维  乘  二维：（矩阵乘法）

shape(2,3)    shape(3,2)       -------------------    shape(2,2)

3. 矩阵  乘  向量：

4. 向量  乘  矩阵：

5. 带有batch，也就是多维的：

shape(4，2,3)    shape(4，3,2)       -------------------    shape(4，2,2)