01背包问题（动态规划）

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<vi,wi≤1000

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

8

思路：

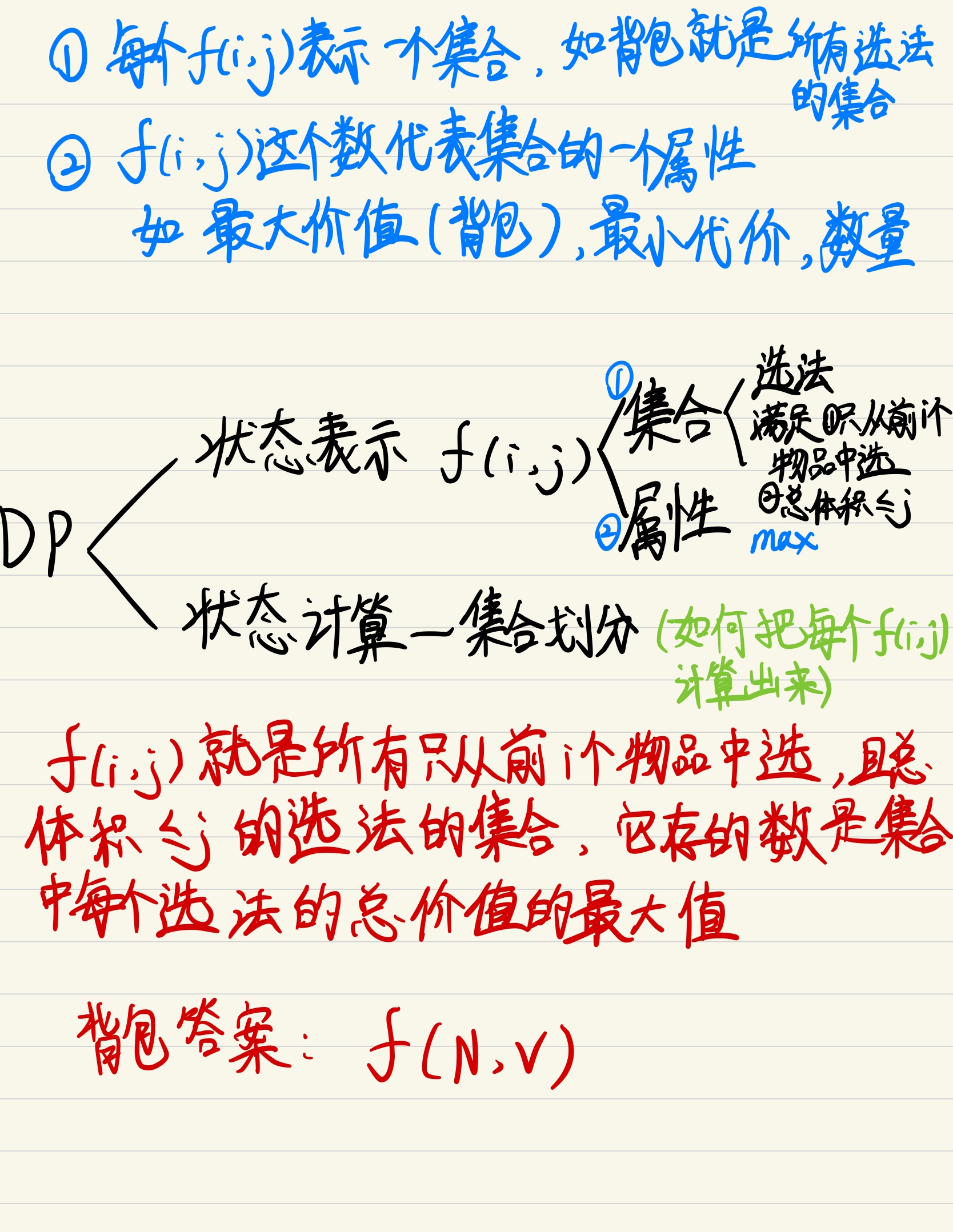
二维的表示：

二维的代码：

#include<iostream>
#include<algorithm>
using namespace std;

const int N=1010;
int n,m;
int V[N],W[N]; //物品的体积和价值
int f[N][N];  //表示前N个物品中选且总体积小于N的选法的集合，这个数代表其中的最大价值

int main()
{
    cin>>n>>m; //表示物品数量和背包容积
    for(int i=1;i<=n;i++) //1到n件物品
    {
        cin>>V[i]>>W[i];
    }

    //f[0][m]==0 从前0个物品选，得到的最大价值是0，没有意义，所以我们从前一个物品开始计算
    for(int i=1;i<=n;i++) //从前1个物品开始选
    {
        for(int j=0;j<=m;j++) 
        {
            //f[i][j]可以分为两个子集，f[i-1][j]和f[i-1][j-vi]+wi 
            //f[i][j]就是左边子集和右边子集取最大

            f[i][j]=f[i-1][j];  //先更新为左边的子集

            //只有当总体积大于等于第i个物品体积时（装不下第i个物品），后面这个子集才有意义
            if(j>=V[i])
            //和右边的子集比较，取最大的

            f[i][j]=max(f[i][j],f[i-1][j-V[i]]+W[i]);

            // cout<<"i:"<<i<<" j:"<<j<<" res:"<<f[i][j]<<endl;
        }
    }

    cout<<f[n][m]<<endl;

    return 0;
}

然而，我们可以把二维的代码简化为一维的，节省空间

 

f[i]表示：在前i个物品中取。
f[j]表示：拿了总体积不超过j的物品，最大总价值。

从二维变为一维：

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j]; 
            
            if(j>=V[i]) f[i][j]=max(f[i][j],f[i-1][j-V[i]]+W[i]); 
        }
    }

先看二维的状态转移方程式

因为f[i]这个维度仅取决于f[i-1]，可以通过外层的i++循环实现，所以可以删掉f[i]这个维度

删除之后：

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[j]=f[j];  //自身赋值给自身，无意义可删
            
            if(j>=V[i]) f[j]=max(f[j],f[j-V[i]]+W[i]); 
        }
    }

而又因为在内层的j循环中，j必须>=v[i]才有意义，才能开始计算，所以j直接从v[i]开始取

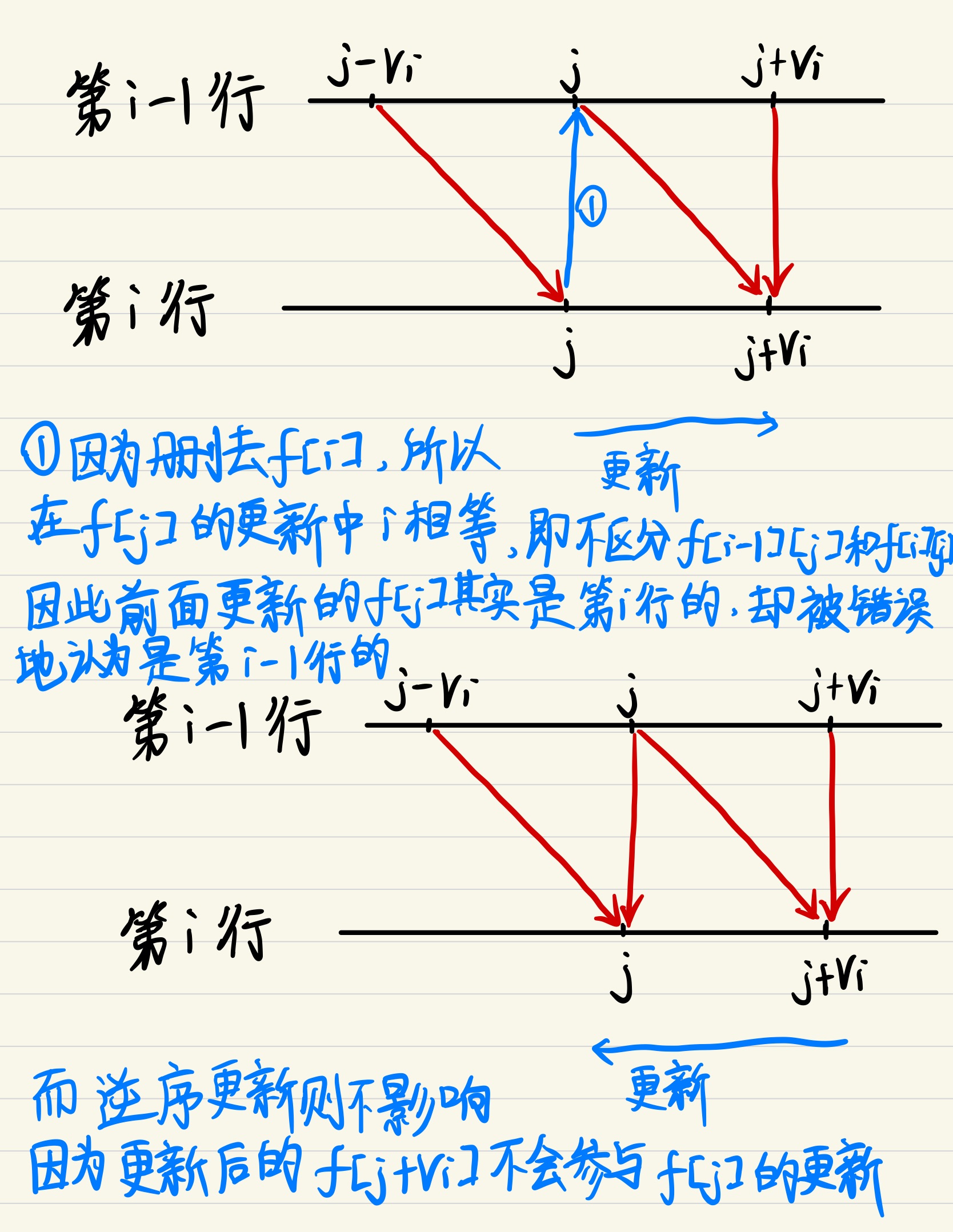
关键是看图，如果用一维表示，则只能表达f[j]，而i相等，这就出现了我们需要第i-1行的f[j]来更新第i行的f[j+vi]，但我们无法正确表示，所以要用逆序让j从后往前更新。

一维的代码：

//优化法
#include<iostream>
#include<algorithm>
using namespace std;

const int N=1010;
int n,m;
int V[N],W[N]; //物品的体积和价值
int f[N];  //表示前N个物品中选且总体积小于N的选法的集合，这个数代表其中的最大价值

int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)
    {
        cin>>V[i]>>W[i];
    }

    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=V[i];j--)
        {
            f[j]=max(f[j],f[j-V[i]]+W[i]);
        }
    }

    cout<<f[m]<<endl;
    return 0;
}

参考：动态规划专题——背包问题_动态规划背包问题-优快云博客