【机器学习】朴素贝叶斯算法

一、概述：

朴素贝叶斯（Naive Bayes）是一种基于贝叶斯定理与特征条件独立假设的分类方法。它之所以被称为“朴素”，是因为它假设了输入特征之间的条件独立性，即一个特征的出现概率与其他特征无关。尽管这个假设在现实中很少成立，但朴素贝叶斯分类器在许多实际应用中仍然表现出了出色的性能。

1.1贝叶斯公式：

通常，事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件下的概率是不一样的；然而，这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
贝叶斯法则是关于随机事件A和B的条件概率和边缘概率的：

其中P(A|B)是在B发生的情况下A发生的可能性。

在这里先讲两个概念：

先验概率（prior probability）：是指根据以往经验和分析得到的概率。

后验概率（posterior probability）：是指在得到“结果”的信息后重新修正的概率。

二、朴素贝叶斯定理：

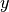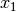给定一个类别  和一个从  到 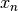 的相关的特征向量， 贝叶斯定理阐述了以下关系:

假设它们之间都是相互独立的：

<