59、螺旋矩阵II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

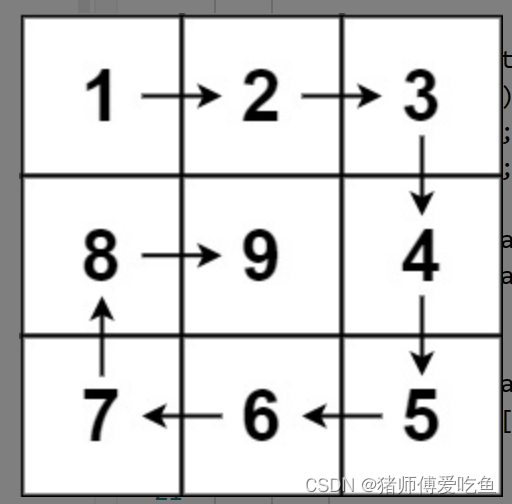
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
示例 2：

输入：n = 1
输出：[[1]]

解法分析：

大家还记得我们在二分法中，如果要写出正确的二分法一定要坚持循环不变量原则。

而求解本题依然是要坚持循环不变量原则。

模拟顺时针画矩阵的过程:

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

由外向内一圈一圈这么画下去。

可以发现这里的边界条件非常多，在一个循环中，如此多的边界条件，如果不按照固定规则来遍历，那就是一进循环深似海，从此offer是路人。

这里一圈下来，我们要画每四条边，这四条边怎么画，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

那么我按照左闭右开的原则，来画一圈，大家看一下：

同一种颜色代表每一个循环时需要遍历的 。共有四个方向的循环

class Solution {

public:

vector<vector<int>> generateMatrix(int n) {

	vector<vector<int>> v(n,vector<int>(n,0));

	int startx=0,starty=0;//代表起始位置

	int loop=n/2;//代表要转的圈数，例如n=3,loop=1,则要转一圈

	int mid=n/2;//代表最中间的数的坐标，例如n=3,mid=1,坐标为(1,1)

	int pos=1;// 需要控制每一条边遍历的长度，每次循环右边界收缩一位

	int i,j,count=1;

	while(loop--){

		i=startx;

		j=starty;

		  //顺时针，从最左最上开始，延四个方向遍历

		  for(j=starty;j<n-pos;j++){

			v[startx][j]=count++;

			}

  

		for(i=startx;i<n-pos;i++){

			v[i][j]=count++;

		}

  
		for(;j>starty;j--){

			v[i][j]=count++;

		}

 
		for(;i>startx;i--){

			v[i][j]=count++;

		}

	  startx++;starty++;

		pos++;

	}

	  if(n%2!=0)v[mid][mid]=count;

		 return v;

}
};