蓝桥杯省赛2020 数字三角形

题目描述

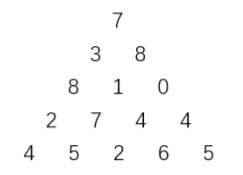
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

输入描述

输入的第一行包含一个整数  (1≤N≤100)，表示三角形的行数。

下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。

输出描述

输出一个整数，表示答案。

输入输出样例

示例

输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

输出

27

dp[i][j]表示0到(i,j)路径的最大值

dp[i][j]+=max(dp[i-1][j-1],dp[i-1][j])+a[i][j]

如果i=1，dp[i][j]+=dp[i-1][j](最左边的数）

如果i=j,dp[i][j]+=dp[i-1][j-1](最右边的数）

因为向左下走的次数与向右下走的次数相差不能超过 1，找到规律：

1.当行数为奇数时，在最中间的一个

2.当行数为偶数时，在中间的两个

n = int(input())
dp = []
for i in range(n):
  now = list(map(int, input().split()))
  dp.append(now)
for i in range(1, n):
    for j in range(i + 1):
        if j == 0:
            dp[i][j] += dp[i - 1][j]
        elif j == i:
            dp[i][j] += dp[i - 1][j - 1]
        else:
            dp[i][j] += max(dp[i - 1][j - 1], dp[i - 1][j])
if n % 2 == 1:
    ans = dp[n - 1][n // 2]
else:
    ans = max(dp[n - 1][n // 2 - 1], dp[n - 1][n // 2])
print(ans)