tarjan算法求解强连通分量问题

Part1：有向图的强连通分量：

一个连通图只有一个联通分量就是自身，非连通图有多个连通分量。

在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。

而有向图G的极大强连通子图S，即添加任意顶点都会导致S失去强连通的属性，则称S为G的强连通分量。

DFS生成树：

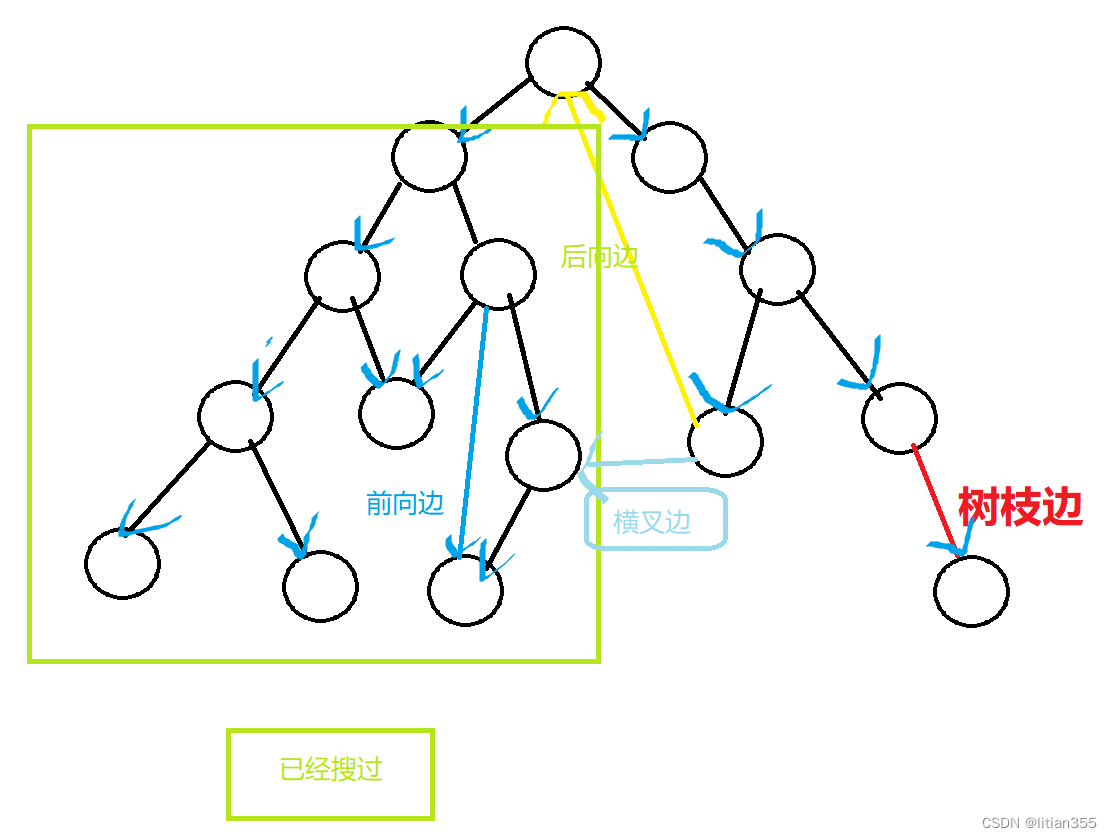
对于一棵的dfs生成树，树边可以分为以下4类：

1.树枝边<x,y> x是y的父节点。

2.前向边<x,y> x是y的祖宗节点。

3.后向边<x,y> 返祖边y是x的祖宗节点。

4.横叉边<x,y> x已经被dfs遍历过，但x不是y的一个祖宗节点

根据DFS生成树如何找到强连通分量：

如果结点 u 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 u为根的子树中。结点 u被称为这个强连通分量的根。

反证法：假设有个结点 v在该强连通分量中但是不在以 u为根的子树中，那么 u到 v的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 u 是第一个访问的结点矛盾了，命题得证。

为了找到强连通分量在搜索树中的第一个节点，我们引入时间戳（timestamp）

Tarjan 算法求强连通分量
在 Tarjan 算法中为每个结点 u维护了以下几个变量：

dfn（u）表示遍历到u时的时间戳；

low（u）表示从u开始遍历到的最小时间戳；

那么如果lo