鸡蛋的硬度蓝桥杯：耐摔指数

最新推荐文章于 2024-02-02 23:32:17 发布

原创最新推荐文章于 2024-02-02 23:32:17 发布 · 300 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #职场和发展 #动态规划 #c++ #算法

文章讨论了一种经典的优化问题——摔鸡蛋，如何在最坏情况下用最少的次数确定鸡蛋的耐摔楼层。作者首先介绍了错误的二分搜索思路，然后通过分析最坏运气的情况，揭示了选择首次投掷楼层的重要性。接着，文章提出了动态规划的解决方案，通过构建记忆数组并遍历所有可能的初始投掷楼层，找到最小检测次数。最后，给出了C++代码实现动态规划算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

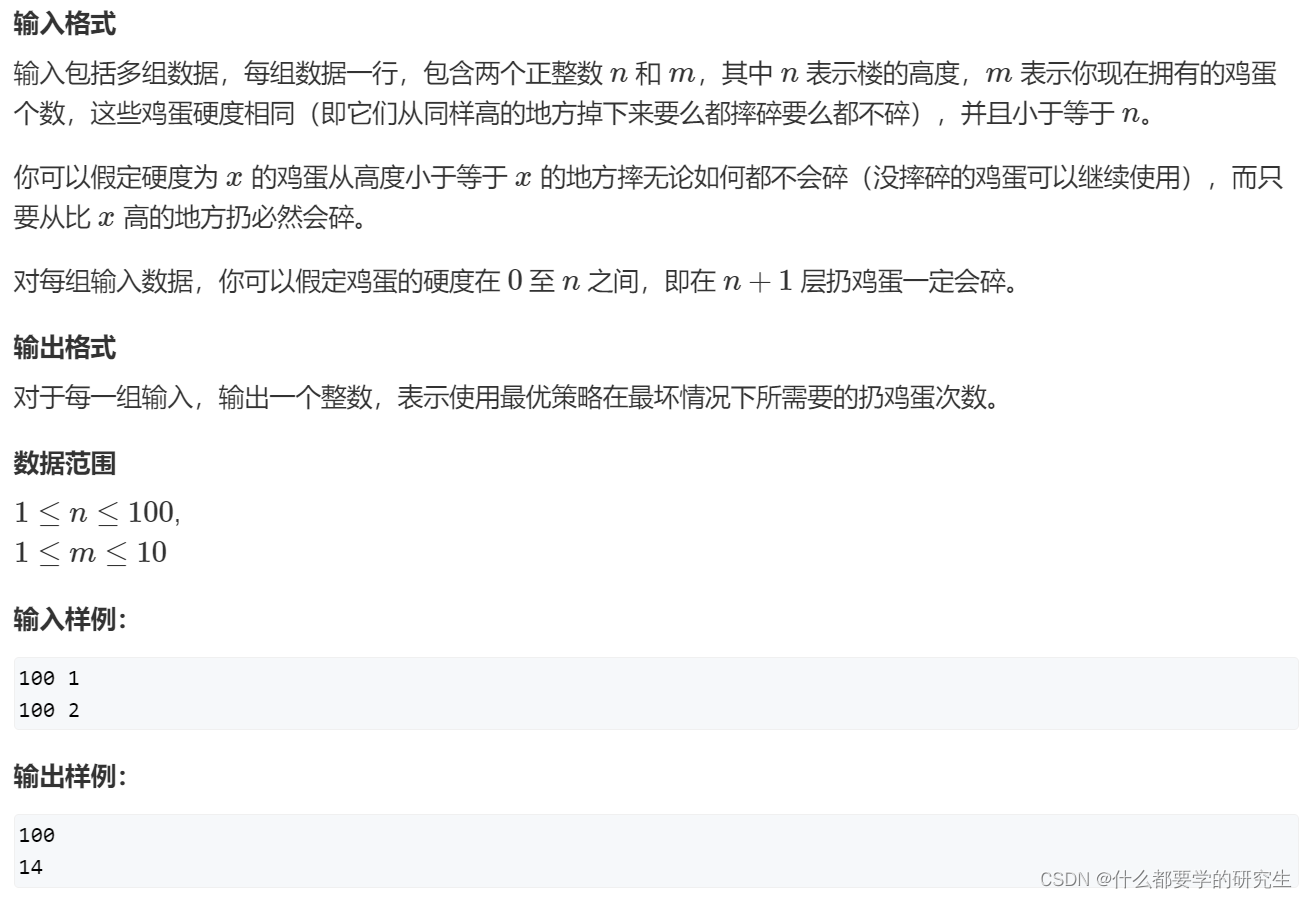
一、题目信息

二、错误的理解

1.总结一下题目中的关键信息

①物品摔坏之后就不能继续测试了，所以当我们只有一个物品时，我们只能从第一层一层一层的进行测试。

2.我首次看到类似的题目是在蓝桥杯的历年真题

摔手机（手机和鸡蛋一样都是易碎物品）：

3.我最开始的思路

就是每次都用手机在二分的层数进行测试，这样就可以把楼层分成两份，进而使用最少的次数得到物品的耐摔度。

那如果楼层很高，而我们前两次手机都摔碎了呢，这时对于剩下的楼层我们就需要一层一层的尝试。

然后当我自信的提交代码之后，发现样例全错，吃土学生只能查看第一个用例，3个手机，150层，只需要10次就能得到结果。

按照我的思路，至少需要2 + 150/2/2 = 39次

我百思不得其解，明明二分就是最好的答案啊，什么人类能够10就得到最终答案。

三、如果走出思维误区

最后但我看到acwing的摔鸡蛋样例的时候，我悟了？

1. 请你思考100层楼，2个鸡蛋，在最优策略，最坏运气，最少需要多少次才能得到结果？

按照刚刚错误的思路进行二分，就是51次或者50次。为什么会有两个答案，因为偶数二分本来mid值就是会有两种取值。

如果我们第一次在51层楼扔下，如果鸡蛋碎了就需要50 + 1 = 51次，而如果我们第一次在50层楼扔下，如果鸡蛋碎了就需要49 + 1 = 50次。

为什么我们不按照鸡蛋没有碎的情况来考虑呢？因为我们知道以上两种情况，鸡蛋碎了比不碎检测剩下的楼层一定需要用到更多的次数，而我们又是最坏运气，所以只能取最大的测试次数。

（如果鸡蛋没碎，同样时剩下50层楼，拥有两个鸡蛋的我们可以继续二分肯定比碎掉的情况用的次数少）

2.通过上述样例的阐述我们可以总结出三件事情

①对于第一次选择从哪个楼层扔下鸡蛋，不同的层数对最终的最少检测次数有很大影响。

②每次扔下鸡蛋，就会产生两种情况，鸡蛋碎了/没碎，由于我们是最坏情况，所以我们只能取两种情况所需要的检测次数的最大值。

③如果我们从中间扔下鸡蛋，碎了比没碎所需的次数要大得多。

四、从动态规划的角度思考并解决问题

所以我们有没有可能得到每次扔下的最佳楼层呢？我们还未能知晓。

1.不过我们可以思考暴力解法

遍历第一次可能扔下的所有楼层，最后把所有情况取最小值，不就能得到最优策略下的最少检测次数吗。

我们设记忆数组为a[N][k]，a[i][j]代表i个鸡蛋，j层楼最少需要多少次能够得到检测结果。那对于i = 1的情况，a[1][j]也就一定是j。（一个鸡蛋，有几层楼就需要检测几次）

以2个鸡蛋，8层楼为例，即求a[2][8]。第一次我们可以从1~8层，8种情况进行扔鸡蛋。

假设我们第一次从6层楼扔下，产生了两种情况：

①如果鸡蛋碎了那对于剩下5层楼只有一个鸡蛋，也就是需要a[1][5]次

②如果鸡蛋没碎那对于剩下2层楼我们还有两个鸡蛋，也就是需要a[2][2]次

对于第一次从6层扔下，我们就需要 max(a[1][5], a[2][2]) + 1次。

但是我们还有其他剩余7种情况啊，所以a[2][8]就是所有这8种情况的最小值。

也就是 a[2][8] = min(for k in 8: max(a[1][k - 1], a[2][8 - k]) + 1)

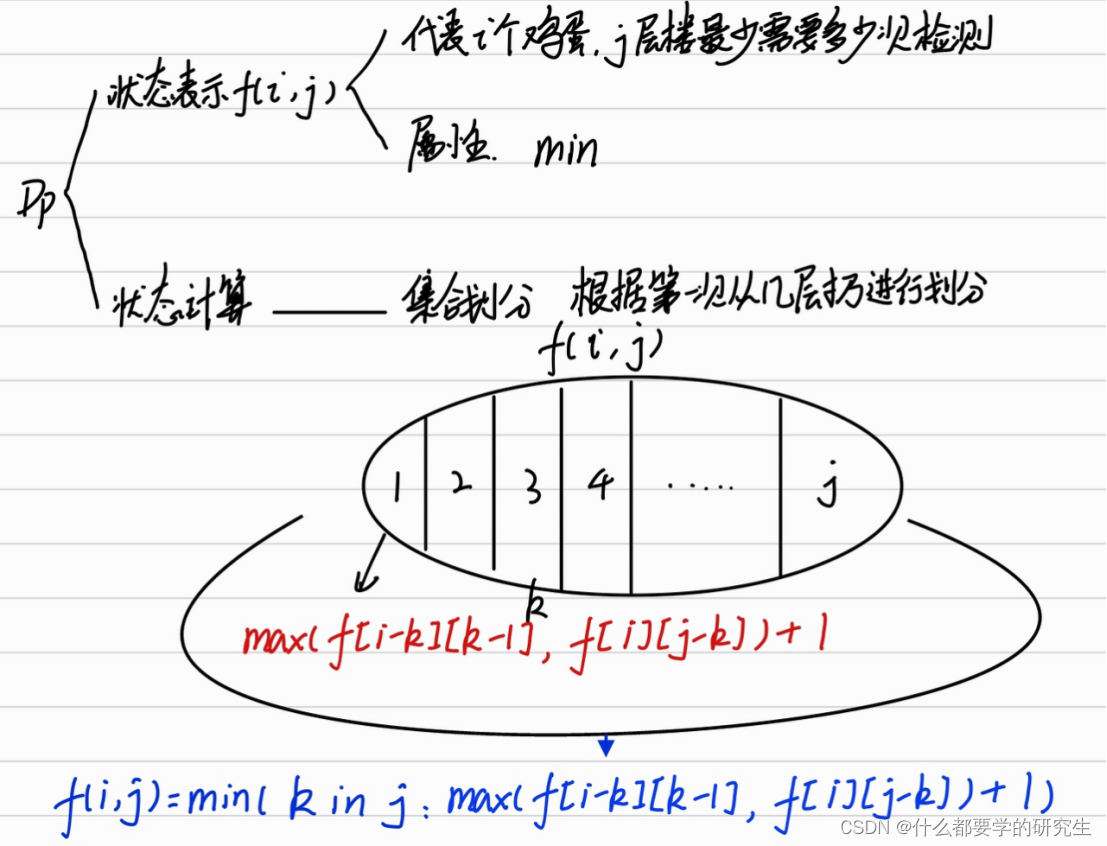
2.最终总结为对于a[i][j]的朴素情况

a[i][j] = min(for k in j: max(a[i - 1][k - 1], a[i][j - k]) + 1 )

k代表第一次从第几层楼扔下去，如果碎了剩下k-1层就需要i-1个鸡蛋进行测试，而如果没碎上层的j-k层还是有i个鸡蛋进行测试。

3.从动态dp的角度考虑

最后按照dp的思路讲解就是，对于a[i][j]可以划分为j种状态，最优解取j种状态结果的最小值，而最坏情况代表着对于每一种状态需要取最大值。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <math.h>

using namespace std;
const int N = 11;
const int M = 110;

int n, k;
int a[N][M];

int main()
{
	while (cin >> k >> n)
	{
		for (int i = 1; i <= k; i++)	a[1][i] = i;
		for (int i = 1; i <= n; i++)	a[i][1] = 1;

		for (int i = 2; i <= n; i++)
		{
			for (int j = 2; j <= k; j++)
			{
				a[i][j] = 1e9;
				for (int k = 1; k <= j; k++)
				{
					int tempt = max(a[i - 1][k - 1], a[i][j - k]) + 1;
					a[i][j] = min(tempt, a[i][j]);
				}
			}
		}

		printf("%d", a[n][k]);
	}

	return 0;
}