储蓄、资本积累与产出

1.产出和资本的相互作用

长期产出水平的决定性因素是产出与资本之间的相互作用。

资本数量决定产出数量。产出数量又决定资本数量，由此决定积累的资本数量。

在规模经济不变的假设下，有人均产出和人均资本的关系式：

人均产出是人均资本的增函数，假定资本规模报酬递减，随着人均资本越来越多，一定量的资本增加对人均产出的影响越来越小。当人均资本达到一定程度的时候。再增加人均资本对人均产出的影响很小。

为了进一步简化，可以将人均产出与人均资本的关系式简化成：

两个假设：

（1）人口规模、参与率和失业率不变；

（2）没有技术进步。

上述两个假设提出后，可以将人均产出和人均资本关系进一步写成：

这样一来，可以看出，人均资本越高，人均产出越高。

2.产出对资本的影响

假设经济体是封闭的，那么投资等于私人储蓄加上公共储蓄，即：

为了更好研究私人行为，这里进一步假定公共储蓄为0，即税收全部用于政府购买：

因此有：

私人储蓄与收入成正比因而。参数s为储蓄率，其值介于0和1之间。

将上述等式合并，可得：

投入与产出成正比：产出水平越高，储蓄率越高，从而投资水平也越高。

假设资本以每年比率的比例折旧，那么资本存量的变化由下式表示，

第t+1年的资本存量等于第t年的资本存量减去折旧加上投资。

整理得到，产出和资本积累的关系可以表示为：

于是有：

整个式子均除以N得到人均资本存量

前面我们提到：

于是：

其中（这里已经假设人口N保持不变）

记

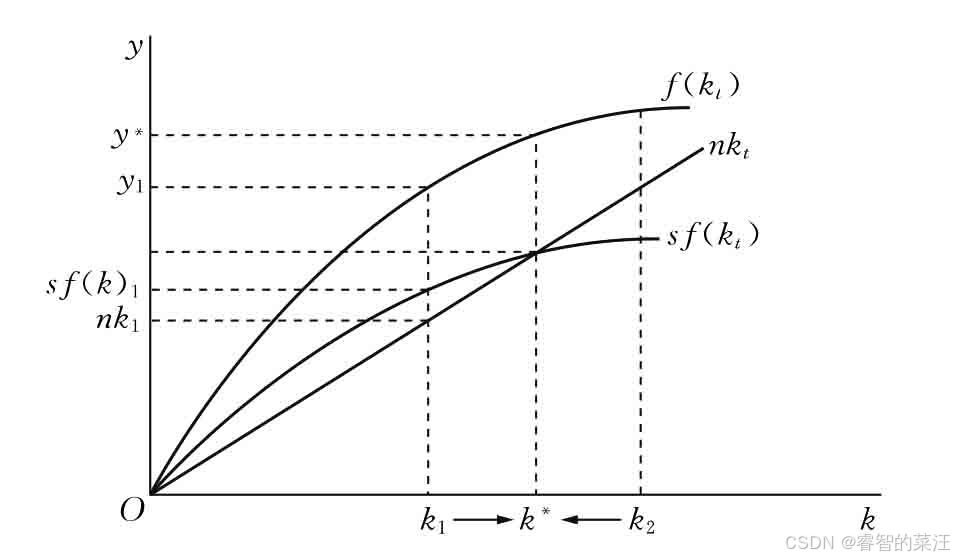
图2.1 产出和资本存量的关系

当储蓄大于资本折旧的时候，资本存量净增加。当储蓄率小于资本折旧的时候，资本存量净减少。

4.稳态资本和产出

单位工人产出和单位工人占有资本不再发生变化的状态称为经济的稳态。此时

且

在图2.1上表示为k*的位置。

5.储蓄率和产出

（1）储蓄率对长期的单位工人产出增长率没有影响，单位工人产出增长率在长期为0.

（2）储蓄率决定长期单位工人产出水平，在其他条件相同的情况下，储蓄率高的国家在长期中会有更高水平的单位工人产出。

（3）储蓄率的上升在一段时间内引起更高的单位工人产出增长，但这种高增长并不能持续到永远。

有技术进步的经济拥有正的单位工人产出增长率，在长期也是如此。这个长期增长率和储蓄率无关；然而储蓄率影响单位工人的产出水平；储蓄率的上升使得增长比稳态增长率更高的速度增长一段时间，直到经济到达更高的路径。

6.政府对储蓄率的影响

（1）政府可以通过改变公共储蓄。给定私人储蓄，正的储蓄率，即预算盈亏导致总储蓄增加；相反，负的公共储蓄，即预算赤字导致总储蓄下降。

（2）政府能用税收影响私人储蓄。

7.黄金律水平

储蓄的增加要以低消费为代价。储蓄率（一直为0）的经济是一个资本等于0的经济。

储蓄率为0，表示长期的消费为0.经济中的储蓄率为1，表示长期消费为0.这两个极端情形表明肯定存在介于0到1之间的某个储蓄率使得稳态时的消费水平达到最大。与使得消费在稳态中达到最高水平的储蓄率相对应的资本水平被称为黄金律的资本水平，此时资本增加或减少均会减少稳态时的消费。

8.定量研究

假定生产函数为：

两边同时除以N得到

于是有：

在稳态下，产出增长为0

得到：

整理得到：

将此结果代入，可以得到稳态产出为：

这表明储蓄率上升或者折旧率降低都能使得稳态下的单位工人占有资本和单位工人产出更高。

在稳态时，工人的消费等于总产出减去折旧

即：

可以解得：单位工人消费为：

9.实物资本与人力资本

引入人力资本后，将生产函数关系改写成如下形式：

单位工人产出水平取决于单位工人占有的事物资本水平和人力资本水平。

社会中以人力资本形式通过教育和培训的储蓄增加，提高稳态时单位工人占有的人力资本，进而引起单位工人产出的增加，在长期中，单位工人产出不仅取决于储蓄的多少，还取决于教育支出的多少。

在没有技术进步的条件下也能形成稳定增长的模型称为内生增长模型，这些模型反映了即使在长期，增长率也依赖于储蓄率和教育支出率等变量。然而，在给定技术进步率下，这些措施不可能永久地维持更高的增长率。