缓存淘汰算法实现

什么是LRU？

LRU我们在学习Redis时听说过，是Redis中一种缓存淘汰策略，不光是Redis很多应用只要牵扯到缓存都要设置缓存淘汰策略。常用到的缓存淘汰策略有FIFO（先入先出）、LRU（最近最少使用）、LFU（最少使用）。

FIFO先入先出就是队列的特性很好实现，今天我们主要讨论后两个。

LRU算法实现

LRU指的是优先淘汰掉最近并没有使用的，举个例子，现在有一个书架只能放10本书，每当你看完一本或者是将书重新看一遍后将他放在书架的最左边，当书架放满后还想要放书的话就要将最右边的书（最不经常看的书）移去。我们通过Leetcode的一道题来进一步分析：

题干是主要意思就像我上面所讲的例子，同时还要实现插入书籍，移除书籍的操作。这里最优的实现方法是双向链表+哈希表，hash表的目的是能快速的找到链表中是否有目标数，如果有则要将他移动到链表头，如果没有就新创建一个节点将他插入链表头的位置。

在双向链表的实现中，使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限，这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。

我们先看容量为3的例子，首先缓存了1，此时结构如图所示。之后再缓存2和3，结构如b所示。

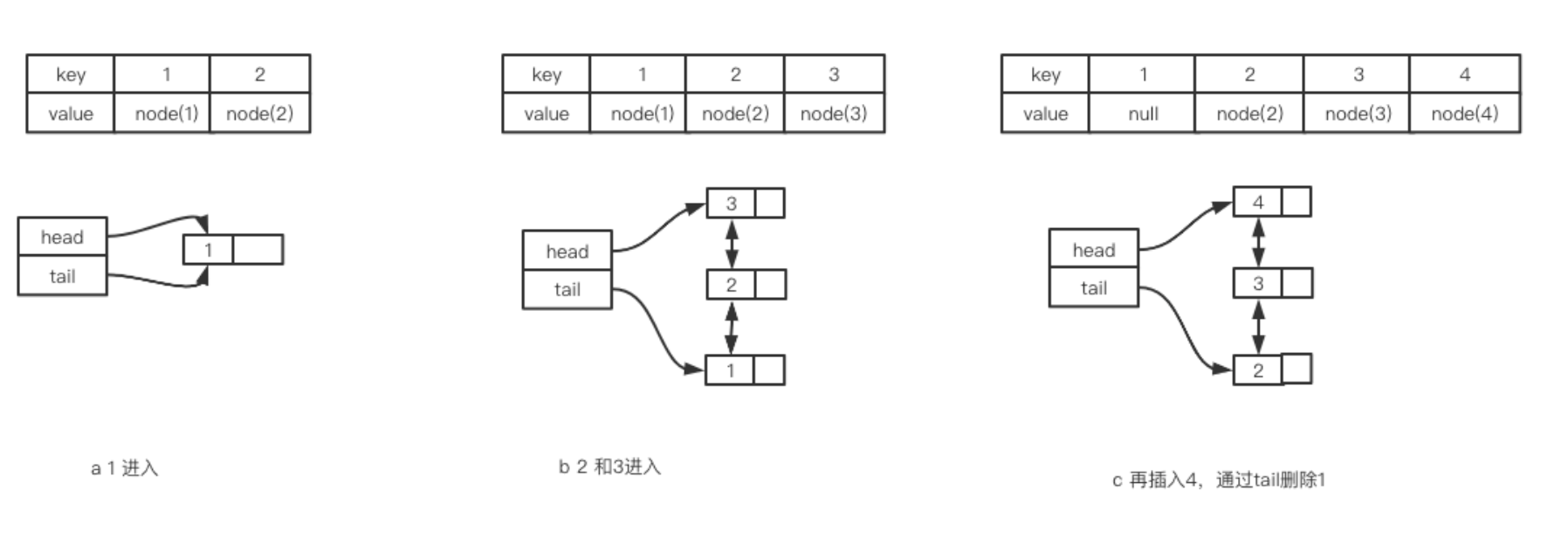
之后4再进入，此时容量已经不够了，只能将最远未使用的元素1删掉，然后将4插入到链表头部。此时就变成了上图c的样子。

接下来假如又访问了一次2，会怎么样呢？此时会将2移动到链表的首部，也就是下图d的样子。

之后假如又要缓存5呢？比时就将tail指向的3删除，然后将5插入到链表头部。也就是上图e的样子。

大致思路是这样的，我们来看代码实现：

class LRUCache {
    //Hash+双向链表方法

    //双向链表
    class DListNode{
        int key;
        int value;
        DListNode prev;
        DListNode next;

        DListNode(){}
        DListNode(int key1,int value1){
            this.key=key1;
            this.value=value1;
        }
    }

    //HashMap
    private Map<Integer,DListNode> cache = new HashMap<Integer,DListNode>();
    //缓存容量
    private int capacity;
    //存入的个数
    private int size;
    //指向链表头和尾的指针
    private DListNode head;
    private DListNode tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.head = new DListNode();
        this.tail = new DListNode();
        this.capacity = capacity;
        head.next = tail;
        tail.prev = head;
    }
    
    public int get(int key) {
        DListNode node = cache.get(key);
        if(node==null){
            return -1;
        }
        moveToHead(node);
        return node.value;
    }
    
    public void put(int key, int value) {
        DListNode node = cache.get(key);
        if(node==null){
            //存入缓存,添加到链表
            DListNode newNode = new DListNode(key,value);
            cache.put(key,newNode);
            addToHead(newNode);
            size++;
            if(size>capacity){
                DListNode deleteNode = removeLastNode();
                cache.remove(deleteNode.key);
                size--;
            }
        }else{
            node.value = value;
            moveToHead(node);
        }
    }

    //添加到头部
    private void addToHead(DListNode node){
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }
    //删除一个节点
    private void removeNode(DListNode node){
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }
    //移动到头部
    private void moveToHead(DListNode node){
        removeNode(node);
        addToHead(node);
    }
    //删除尾部
    private DListNode removeLastNode(){
        DListNode node = tail.prev;
        removeNode(node);
        return node;
    }
}

要注意区分好链表未满、链表已满、插入数据已存在这三种情况。

LFU算法实现

首先要搞清楚LFU和LRU的区别？

同样我们还是拿书架举例，LFU更侧重于次数，看过一次的数就是要比看过两次的数先淘汰，比如书架上有9本书都看过了两次，现在放入了一个看过一次的新书，当又有新书来的时候会淘汰掉那本看过一次的书。想要实现LFU算法我们需要用准备多个书架，根据书籍看的次数决定放在那个书架，只有当低频率书架的书淘汰完以后才会淘汰高频率书架上的书。

当然我们会再开一个hash表为了记录不同频率书架上的第一本书，方便书籍的移动，同时删除时删除的是链表的尾节点。每个链表长度的总和就是缓存的大小。

class LFUCache {
    private static class Node {
        int key, value, freq = 1; // 新书只读了一次
        Node prev, next;

        Node(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }

    private final int capacity;
    private final Map<Integer, Node> keyToNode = new HashMap<>();
    private final Map<Integer, Node> freqToDummy = new HashMap<>();
    private int minFreq;

    public LFUCache(int capacity) {
        this.capacity = capacity;
    }

    public int get(int key) {
        Node node = getNode(key);
        return node != null ? node.value : -1;
    }

    public void put(int key, int value) {
        Node node = getNode(key);
        if (node != null) { // 有这本书
            node.value = value; // 更新 value
            return;
        }
        if (keyToNode.size() == capacity) { // 书太多了
            Node dummy = freqToDummy.get(minFreq);
            Node backNode = dummy.prev; // 最左边那摞书的最下面的书
            keyToNode.remove(backNode.key);
            remove(backNode); // 移除
            if (dummy.prev == dummy) { // 这摞书是空的
                freqToDummy.remove(minFreq); // 移除空链表
            }
        }
        node = new Node(key, value); // 新书
        keyToNode.put(key, node);
        pushFront(1, node); // 放在「看过 1 次」的最上面
        minFreq = 1;
    }

    private Node getNode(int key) {
        if (!keyToNode.containsKey(key)) { // 没有这本书
            return null;
        }
        Node node = keyToNode.get(key); // 有这本书
        remove(node); // 把这本书抽出来
        Node dummy = freqToDummy.get(node.freq);
        if (dummy.prev == dummy) { // 抽出来后，这摞书是空的
            freqToDummy.remove(node.freq); // 移除空链表
            if (minFreq == node.freq) {
                minFreq++;
            }
        }
        pushFront(++node.freq, node); // 放在右边这摞书的最上面
        return node;
    }

    // 创建一个新的双向链表
    private Node newList() {
        Node dummy = new Node(0, 0); // 哨兵节点
        dummy.prev = dummy;
        dummy.next = dummy;
        return dummy;
    }

    // 在链表头添加一个节点（把一本书放在最上面）
    private void pushFront(int freq, Node x) {
        Node dummy = freqToDummy.computeIfAbsent(freq, k -> newList());
        x.prev = dummy;
        x.next = dummy.next;
        x.prev.next = x;
        x.next.prev = x;
    }

    // 删除一个节点（抽出一本书）
    private void remove(Node x) {
        x.prev.next = x.next;
        x.next.prev = x.prev;
    }
}