【学习笔记】第四章概率论与数理统计

原创已于 2022-02-10 19:49:31 修改 · 2.6k 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#概率论 #机器学习 #人工智能

于 2022-01-24 22:58:40 首次发布

司守奎老师 python数学建模专栏收录该内容

6 篇文章

订阅专栏

这篇博客详细介绍了概率论与数理统计的主要内容，包括随机变量的概率计算与数字特征，描述性统计知识，如样本、总体、直方图和统计量，以及参数估计和假设检验的原理与方法。通过实例展示了如何计算统计量、绘制统计图，并探讨了方差分析的应用。此外，还讲解了非参数检验中的分布拟合检验和Kolmogorov-Smirnov检验。

4.3.2 参数假设检验（知道总体服从什么类型的分布）

1. 单个总体均值的假设检验

4.3.3 非参数假设检验（不知道总体服从什么类型的分布）

1. 分布拟合检验（检验法）

2. Kolmogorov-Smirnov检验

4.4 方差分析

4.4.1 单因素方差分析及python实现

4.4.2 双因素方差分析及python实现

1. 数学模型

4.1 随机变量的概率计算和数字特征

4.1.1 随机变量的概率计算

例4.1 设 $X\sim N(3,5^2)$ (1）求P{2<X<6}；（2）确定c，使P{-3c<X<2c}=0.6

from scipy.stats import norm
from scipy.optimize import fsolve
print("p=",norm.cdf(6,3,5)-norm.cdf(2,3,5))#做差，后减前
f=lambda c: norm.cdf(2*c,3,5)-norm.cdf(-3*c,3,5)-0.6
print("c=",fsolve(f,0))

定义4.1 α分位数

若连续型随机变量X的分布函数为 $F(x)$ ,对于0<α<1,若 $x_\alpha$ 使得 $P\left \{ X\leq x_\alpha \right \}=\alpha$ ,则称 $x_\alpha$ 为这个分布的α分位数。若 $F(x)$ 的反函数 $F^{-1}(x)$ 存在,则有 $x_\alpha =F^{-1}(1-\alpha )$

定义4.2 上α分位数

若连续型随机变量X的分布函数为 $F(x)$ ，对于 $0<\alpha <1$ ,若 $\tilde{x}_\alpha$ 使得 $P\left \{ X>\tilde{x}_\alpha \right \}=\alpha$ ，则称 $\tilde{x}_\alpha$ 为这个分布的上α分位数。 若 $F(x)$ 的反函数 $F^{-1}(x)$ 存在,则有 $\tilde{x}_\alpha =F^{-1}(1-\alpha )$

例4.2 设 $X\sim N(0,1)$ ,若 $z_\alpha$ 满足条件 $P\left \{X > z_\alpha \right \}= \alpha ,0<\alpha <1$ ，则称 $z_\alpha$ 为标准正态分布的上α分位数。试计算几个常用的 $z_\alpha$ 的值,并画出 $z_{0.1}$ 的示意图.
计算得到几个常用的 $z_\alpha$ 的值见下表， $z_{0.1}$ 的示意图见下图：

from scipy.stats import norm
from pylab import plot,fill_between,show,text,savefig,rc 
from numpy import array, linspace, zeros
alpha=array([0.001, 0.005, 0.01, 0.025, 0.05, 0.10])#表中给的alpha的值
za=norm.ppf(1-alpha,0,1)  #求上alpha分位数  #定义4.2
print("上alpha分位数分别为", za)
x=linspace(-4, 4, 100); y=norm.pdf(x, 0, 1)
rc('font',size=16); rc('text',usetex=True)
plot(x,y)  #画标准正态分布密度曲线
x2=linspace(za[-1],4,100)#在0.1对应的上alpha分位数和4之间取100个点
y2=norm.pdf(x2);
y1=[0]*len(x2)
fill_between(x2, y1, y2, color='r')  #y1,y2对应的点之间填充
plot([-4,4],[0,0])  #画水平线    # [-4,0]|[4,0]
text(1.9, 0.07, "$\\leftarrow\\alpha$=0.1")  #标注
savefig("figure4_2.png", dpi=500); show()

4.1.2 随机变量数字特征简介

定义4.3：设随机变量X的分布律为： $P\left \{ X=x_k \right \}=p_k,k=1,2,\cdots ,$

若级数 $\sum_{k=1}^{\infty }x_kp_k$ 绝对收敛，则称级数 $\sum_{k=1}^{\infty }x_kp_k$ 的和为随机变量X的数学期望，记为 $E(X)$ ,即 $E(X)=\sum_{k=1}^{\infty }x_kp_k$

定义4.4：设X是一个随机变量，若 $E\left \{ [X-E(X)]^2 \right \}$ 存在，则称 $E\left \{ [X-E(X)]^2 \right \}$ 为X的方差，记为D(X)或Var(X)，即：

$D(X)=Var(X)=E\left \{ [X-E(X)]^2 \right \}$

$\sigma (x)=\sqrt{D(X)}$ 称为标准差或均方差。

方差其实就是随机变量X的函数 $g(X)= [X-E(X)]^2$ 的数学期望

定义4.5：随机变量X的偏度和峰度指的是X的标准化变量 $(X-E(X))/\sqrt{D(X)}$ 的三阶中心距和四阶中心矩：

$v_1=E[(\frac{X-E(x)}{\sqrt{D(X)}})^3]=\frac{E[(X-E(X))^3]}{(D(X))^2}$

$v_2=E[(\frac{X-E(x)}{\sqrt{D(X)}})^4]=\frac{E[(X-E(X))^4]}{(D(X))^2}$

定义4.6： $E\{[X-E(X)][Y-E(Y)]\}$ 称为随机变量X与Y的协方差，记为Cov(X,Y)，即

$Cov(X,Y)=E\{[X-E(X)][Y-E(Y)]\}$

而 $\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$ 称为随机变量X与Y的相关系数。、

定义4.7：k阶矩，中心矩，混合矩，混合中心矩

定义4.8：协方差矩阵

重要分布的数学期望和方差公式：

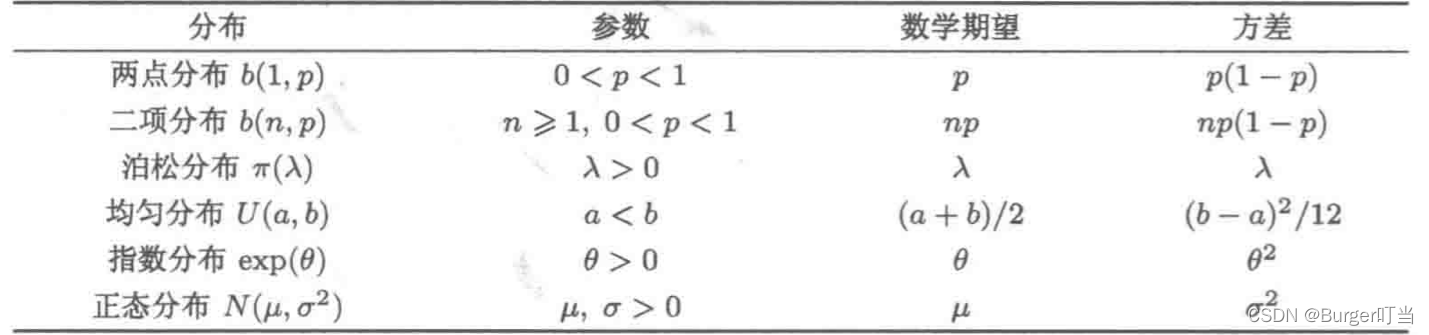
4.1.3 随机变量数字特征计算及应用

例4.3 计算二项分布b(20,0.8)的均值和方差：

from scipy.stats import binom
n, p=20, 0.8
print("期望和方差分布为：", binom.stats(n,p))

即：期望为16，方差为3.2

例4.4 计算二项分布b(20,0.8)的均值、方差、偏度、峰度。

from scipy.stats import binom
n, p=20, 0.8
mean, variance, skewness, kurtosis=binom.stats(n, p, moments='mvsk') 
#上述语句不显示，只为了说明数据顺序
print("所求的数字特征为：", binom.stats(n, p, moments='mvsk'))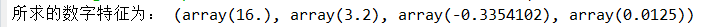

即均值，方差，偏度，峰度分别为16，3.2，-0.3354，0.0125。

例4.5 某路政部门负责城市某条道路的路灯维护.更换路灯时,需要专用云梯车进行线路检测和更换灯泡,向相应的管理部门提出电力使用和道路管制申请,还要向雇用的各类人员支付报酬等,这些工作需要的费用往往比灯泡本身的费用更高,灯泡坏1个换1个的办法是不可取的.根据多年的经验,他们采取整批更换的策略,即到一定的时间,所有灯泡无论好与坏全部更换.
上级管理部门通过监察灯泡是否正常工作对路政部门进行管理,一旦出现1个灯泡不亮,管理部门就会按照折合计时对他们进行罚款.
现抽查某品牌灯泡200个,假设其寿命服从 N(4000,1002)(单位: h)分布,每个灯泡的更换费用(包括灯泡的成本和安装时分摊到每个灯泡的费用)为80元,管理部门对每个不亮的灯泡制订的惩罚费用为0.02元/h,应多长时间进行一次灯泡的全部更换.

from scipy.integrate import quad
from numpy import exp, sqrt, pi, abs
a=80; b=0.02; BD=a/b; mu=4000; s=100
y=lambda x: x*exp(-(x-mu)**2/(2*s**2))/sqrt(2*pi)/s   #定义积分的被积函数
I=0; x1=0; x2=10000
while abs(I-BD)>1E-16:
    c=(x1+x2)/2
    I=quad(y,-10000,c)[0] #由3sigma准则这里积分下限取为-10000,取零效果一样
    if I>BD: x2=c
    else: x1=c
print("最佳更换周期为：", c)

4.2 描述性统计和统计图

4.2.1 统计的基础知识

1. 样本和总体

2. 频数表和直方图

3. 统计量

（1）表示位置的统计量：算数平均值和中位数

算术平均值（简称均值）是描述数据取值的平均位置，记作 $\bar{x}$ ,公式： $\bar{x}=\frac{1}{n}\sum_{i=1}^{n}(x_i)$

中位数是数据由小到大排序后位于中间位置的那个数值，当n为偶数时，取值为中间两数的算术平均值

（2）表示变异程度的统计量： 标准差、方差和极差

标准差s定义为： $s=[\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2]^\frac{1}{2}$ ，它是各个数据与均值偏离程度的度量，这种偏离不妨成为变异。

方差是标准差的平方。

极差是样本最大值与最小值的差。

（3）表示分布形状的统计量：偏度和峰度

偏度： $v_1=\frac{1}{s^3}\sum_{i=1}^{n}(x_i-\bar{x})^3$

峰度： $v_2=\frac{1}{s^4}\sum_{i=1}^{n}(x_i-\bar{x})^4$

（4）协方差和相关系数

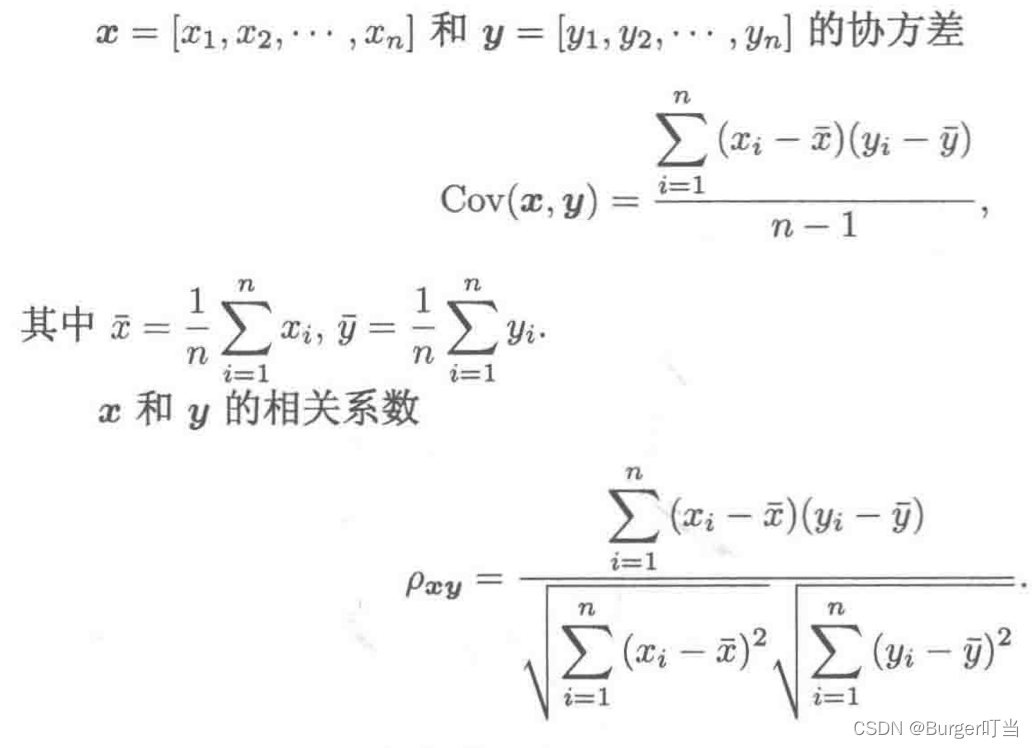
4.2.2 用python计算统计量

1. 使用Numpy计算统计量

Numpy库中计算统计量的函数

例4.6 学校随机抽取100名学生，测量他们的身高和体重，所得数据如表所示（略），试分别求身高的均值，中位数，极差，方差，标准差；计算身高与体重的协方差、相关系数。

from numpy import reshape, hstack, mean, median, ptp, var, std, cov, corrcoef
import pandas as pd
df = pd.read_excel("Pdata4_6_1.xlsx",header=None)
a=df.values  #提取数据矩阵
h=a[:,::2]  #提取奇数列身高
w=a[:,1::2]  #提取偶数列体重
h=reshape(h,(-1, 1)) #转换成列向量，自动计算行数
w=reshape(w,(-1, 1)) #转换成列向量，自动计算行数
hw=hstack([h,w])  #构造两列的数组
print([mean(h),median(h),ptp(h),var(h),std(h)])  #计算均值,中位数,极差,方差,标准差
print("协方差为：{}\n相关系数为：{}".format(cov(hw.T)[0,1],corrcoef(hw.T)[0,1]))

2. 使用Pandas的DataFrame计算统计量

Pandas的DataFrame数据结构为我们提供了若干统计函数，下标给出了部分统计量的方法：

例4.7 （续例4.6）使用 pandas的describe方法计算相关统计量，并计算身高和体重的偏度，峰度，样本的25%,50%,90%分位数。

from numpy import reshape, c_
import pandas as pd
df = pd.read_excel("Pdata4_6_1.xlsx",header=None)
a=df.values; h1=a[:,::2]; w1=a[:,1::2]
h2=reshape(h1,(-1, 1)); w2=reshape(w1,(-1, 1))
df2=pd.DataFrame(c_[h2,w2],columns=["身高","体重"])  #构造数据框
print("求得的描述统计量如下：\n",df2.describe())
print("偏度为：\n",df2.skew())
print("峰度为：\n",df2.kurt())
print("分位数为：\n",df2.quantile(0.9))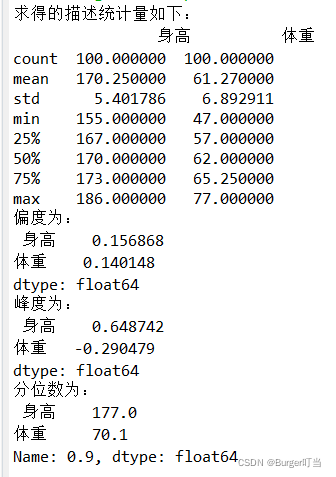

4.2.3 统计图

1. 频数图及直方图

计算频数并且画直方图的命令为：

hist(x,bins=None,range=None,density=None,weights=None,cumulative=False,bottom=None,

histtype='bar' ,align='mid ' ,orientation='vertical ' , rwidth=None，logFalse,color=None,label=None,stacked=False)

他将区间[min(x),max(x)]等分为bins份，统计在每个左闭右开小区间（最后一个区间为闭区间）上的数据出现的频数并画直方图。其中一些参数含义如下：

例4.8（续4.6）画出身高和体重的直方图，并统计从最小体重到最大体重，等间距分为6个小区间，数据出现在每个小区间的频数。

import numpy as np
import matplotlib.pyplot as plt
a=np.loadtxt("Pdata4_6_2.txt")
h=a[:,::2]; w=a[:,1::2]
h=np.reshape(h,(-1,1)); w=np.reshape(w,(-1,1))
plt.rc('font',size=16); plt.rc('font',family="SimHei")
plt.subplot(121); plt.xlabel("身高"); plt.hist(h,10) #只画直方图不返回频数表
plt.subplot(122); ps=plt.hist(w,6)  #画图并返回频数表ps
plt.xlabel("体重"); print("体重的频数表为：", ps)
plt.savefig("figure4_8.png", dpi=500); plt.show()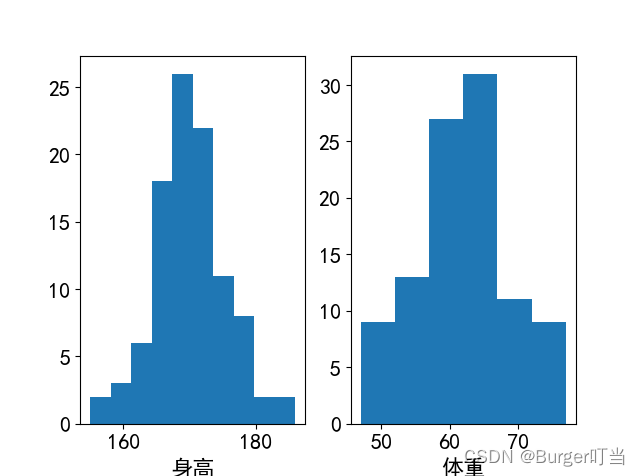

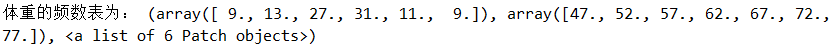
2. 线箱图

定义4.9 样本分位数:

定义：箱线图

例4.9 下面分别给出了25个男子和25个女子的肺活量数据（以L计，数据已经排过序）（略），请画出线相图

import numpy as np
import matplotlib.pyplot as plt
a=np.loadtxt("Pdata4_9.txt")  #读入两行的数据
b=a.T  #转置成两列的数据
plt.rc('font',size=16); plt.rc('font',family='SimHei')
plt.boxplot(b,labels=['女子','男子'])
plt.savefig('figure4_9.png', dpi=500); plt.show()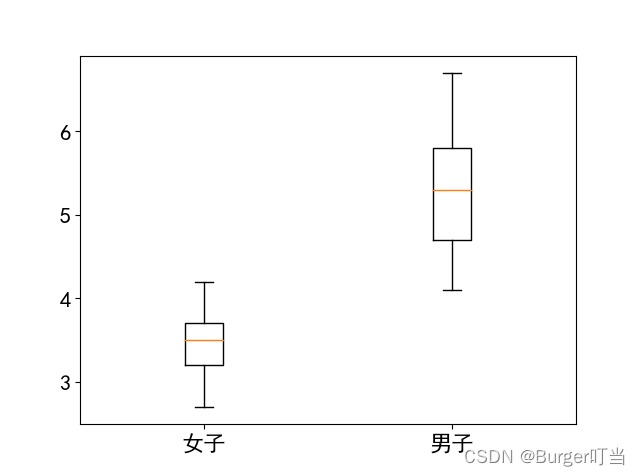

箱线图特别适用于比较两个或两个以上数据集的性质,为此,将几个数据集的箱线图画在同一个图形界面上.例如,在图4.4中可以明显地看到男子的肺活量要比女子的肺活量大,男子的肺活量较女子的肺活量分散.

疑似异常值：

在数据集中某一个观察值不寻常地大于或小于该数集中的其他数据,称为疑似异常值.疑似异常值的存在,会对随后的计算结果产生不适当的影响.检查疑似异常值并加以适当的处理是十分必要的.
第一四分位数Q1与第三四分位数Q3之间的距离:Q3-Q1记为_IOR,称为四分位数间距．若数据小于Q1-1.5IQR或大于Q3＋ 1.5IQR,就认为它是疑似异常值.

例4.10（续例4.6）画身高和体重的箱线图

import numpy as np
import matplotlib.pyplot as plt
a=np.loadtxt("Pdata4_6_2.txt")
h=a[:,::2]; w=a[:,1::2]
h=np.reshape(h,(-1,1)); w=np.reshape(w,(-1,1))
hw=np.hstack((h,w)); plt.rc('font',size=16)
plt.rc('font',family='SimHei')
plt.boxplot(hw,labels=['身高','体重'])
plt.savefig("figure4_10.png",dpi=500); plt.show()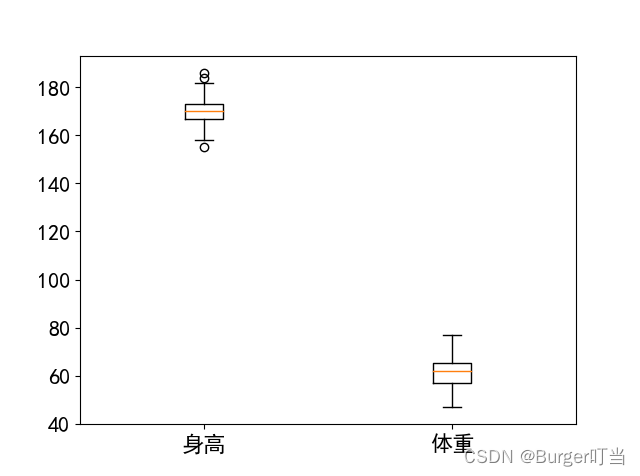

3. 经验分布函数

例4.11（续4.6）画出体重的经验分布函数图形

import numpy as np
import matplotlib.pyplot as plt
a=np.loadtxt("Pdata4_6_2.txt")
w=a[:,1::2]; w=np.reshape(w,(-1,1)); plt.rc('font',size=16)
h=plt.hist(w,20,density=True, histtype='step', cumulative=True)
print(h); plt.grid()
plt.savefig("figure4_11.png",dpi=500); plt.show()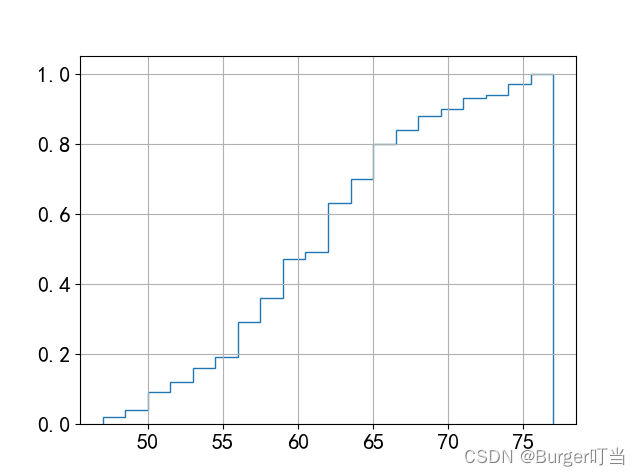

4. Q-Q图

Q-Q图是检验拟合优度的好方法，目前在国内外广泛使用

例4.12 对于例4.6中的身高数据，如果他们来自于正态分布，求该正态分布的参数，试画出他们的Q-Q图，判断拟合效果。、

（1）用矩估计法估计参数的取值，算出样本的均值和标准差

（2）画Q-Q图

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, probplot
a=np.loadtxt("Pdata4_6_2.txt")
h=a[:,::2]; h=h.flatten()
mu=np.mean(h); s=np.std(h); print([mu,s])#求样本均值和方差
sh=np.sort(h) #按从小到大排序
n=len(sh); xi=(np.arange(1,n+1)-1/2)/n
yi=norm.ppf(xi,mu,s)
plt.rc('font',size=16);plt.rc('font',family='SimHei')
plt.rc('axes',unicode_minus=False) #用来正常显示负号
plt.subplot(121); plt.plot(yi, sh, 'o', label='QQ图');
plt.plot([155,185],[155,185],'r-',label='参照直线')
plt.legend(); plt.subplot(122)
res = probplot(h,plot=plt)
plt.savefig("figure4_12.png",dpi=500); plt.show()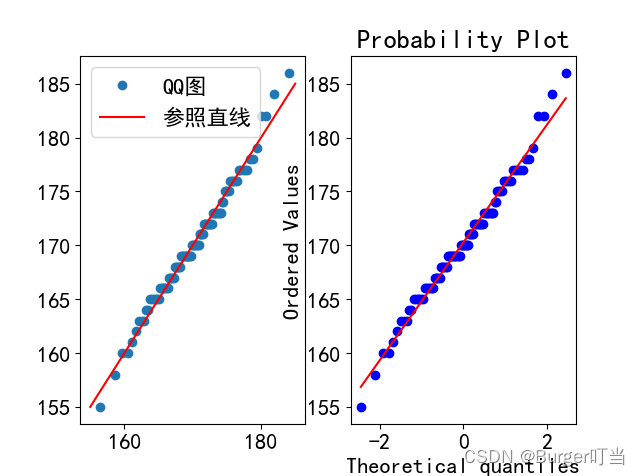

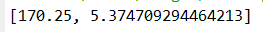
4.3 参数估计和假设检验

4.3.1 参数估计

1. 极大似然估计

例4.13 假定例4.6中学生的身高服从正态分布，求总体均值和标准差的极大似然估计。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
a=np.loadtxt("Pdata4_6_2.txt")
h=a[:,::2]; h=h.flatten()
mu=np.mean(h); s=np.std(h);
print("样本均值和标准差为：",[mu,s])
print("极大似然估计值为：", norm.fit(h))

2. 区间估计

定义：样本均值的标准误差（SEM）

例4.14 有一大批糖果，现从中选择16袋，称得重量（以g计）如下（略），设袋装糖果的重量近似的服从正态分布，试求总体均值 $\mu$ 的置信水平为0.95的置信区间。

from numpy import array, sqrt
from scipy.stats import t
a=array([506,  508,  499,  503,  504,  510,  497,  512,
514,  505,  493,  496,  506,  502,  509,  496])
# ddof取值为1时，标准偏差除的是(N-1)；NumPy中的std计算默认是除以N
mu=a.mean(); s=a.std(ddof=1)  #计算均值和标准差
print(mu, s); alpha=0.05; n=len(a)
val=(mu-s/sqrt(n)*t.ppf(1-alpha/2,n-1),mu+s/sqrt(n)*t.ppf(1-alpha/2,n-1))
print("置信区间为：",val)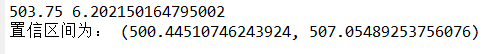

或者可以直接调用库函数求置信区间：

import numpy as np
import scipy.stats as ss
from scipy import stats
a=np.array([506,  508,  499,  503,  504,  510,  497,  512,
514,  505,  493,  496,  506,  502,  509,  496])
alpha=0.95; df=len(a)-1
ci=ss.t.interval(alpha,df,loc=a.mean(),scale=ss.sem(a))
print("置信区间为：",ci)

4.3.2 参数假设检验（知道总体服从什么类型的分布）

1. 单个总体均值的假设检验

（1）正态总体标准差 $\sigma$ 已知的Z检验法

例4.15 某车间用一台包装机包装糖果.包得的袋装糖重是一个随机变量,它服从正态分布.当机器正常时,其均值为0.5kg,标准差为0.015kg.某日开工后为检验包装机是否正常,随机地抽取它所包装的糖9袋,称得净重(kg)为
0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512问机器是否正常?

import numpy as np
from statsmodels.stats.weightstats import ztest
sigma=0.015
a=np.array([0.497, 0.506, 0.518, 0.524, 0.498, 0.511, 0.520, 0.515, 0.512])
tstat1, pvalue=ztest(a,value=0.5)  #计算T统计量的观测值及p值
tstat2=tstat1*a.std(ddof=1)/sigma  #转换为Z统计量的观测值
print('t值为：',round(tstat1,4))
print('z值为：',round(tstat2,4)); print('p值为:',round(pvalue,4))

（2）正态总体标准差 $\sigma$ 未知的 t 检验法

例4.16 某批矿砂的5个样品中的镍含量（%),经测定为3.25 3.27 3.24 3.26 3.24
设测定值总体服从正态分布,但参数均未知,问在α=0.01下能否接受假设:这批矿砂的镍含量的均值为3.25.

import numpy as np
from statsmodels.stats.weightstats import ztest
a=np.array([3.25, 3.27, 3.24, 3.26, 3.24])
tstat, pvalue=ztest(a,value=3.25)
print('检验统计量为：',tstat); print('p值为:',pvalue)

例4.18 分别给出两位文学家马克·吐温(Mark Twain的8篇小品文以及斯诺特格拉斯(Snodgrass)的10篇小品文中由3个字母组成的单词的比例.

两位作家作品中单词统计数据
马克·吐温 0.225 0.262 0.217 0.240 0.230 0.229 0.235 0.217
斯诺特格拉斯 0.209 0.205 0.196 0.210 0.202 0.207 0.224 0.223 0.220 0.201
设两组数据分别来自正态总体,且两总体方差相等,但参数均未知.两样本相互独立．问两位作家所写的小品文中包含由3个字母组成的单词的比例是否有显著的差异(取α =0.05)?

import numpy as np
from statsmodels.stats.weightstats import ttest_ind
a=np.array([0.225, 0.262, 0.217, 0.240, 0.230, 0.229, 0.235, 0.217])
b=np.array([0.209, 0.205, 0.196, 0.210, 0.202, 0.207,
            0.224, 0.223, 0.220, 0.201])
tstat, pvalue, df=ttest_ind(a, b, value=0)
print('检验统计量为：',tstat); print('p值为:',pvalue)
print('自由度为：',df)

4.3.3 非参数假设检验（不知道总体服从什么类型的分布）

1. 分布拟合检验（ $\chi^2$ 检验法）

例4.19 根据某市公路交通部门某年上半年交通事故记录,统计得星期一至星期日发生交通事故的次数如表4.8所示.试检验交通事故的发生次数是否服从离散均匀分布,即交通事故的发生与星期几无关.

import numpy as np
import scipy.stats as ss 
bins=np.arange(1,8)
mi=np.array([36, 23, 29, 31, 34, 60, 25])
n=mi.sum(); p=np.ones(7)/7
cha=(mi-n*p)**2/(n*p); st=cha.sum()
bd=ss.chi2.ppf(0.95,len(bins)-1) #计算上alpha分位数
print("统计量为：{}，临界值为：{}".format(st,bd))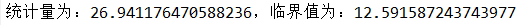

例4.20某车间生产滚珠,随机地抽出」50粒,测符它的且江(平: )为
15.0 15.8 15.2 15.1 15.9 14.7 14.8 15.5 15.6 15.3
15.1 15.3 15.0 15.6 15.7 14.8 14.5 14.2 14.9 14.9
15.2 15.0 15.3 15.6 15.1 14.9 14.2 14.6 15.8 15.2
15.9 15.2 15.0 14.9 14.8 14.5 15.1 15.5 15.5 15.1
15.1 15.0 15.3 14.7 14.5 15.5 15.0 14.7 14.6 14.2
经过计算知样本均值 $\bar{x}$ = 15.0780,样本标准差s=0.4282,试问滚珠直径是否服从正态分布N(15.0780, $0.4282^2$ )( $\alpha$ = 0.05)?

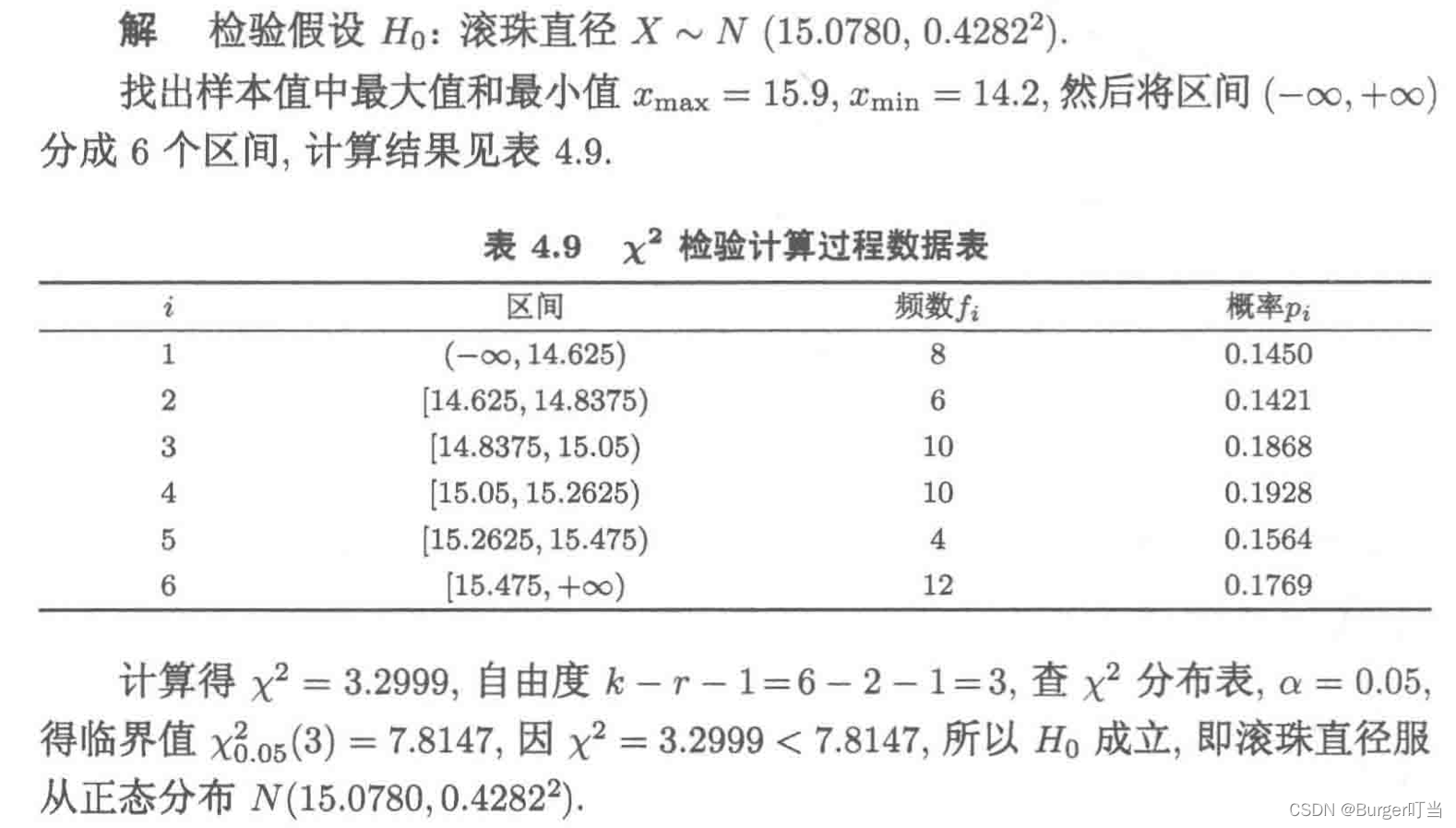
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ss
n=50; k=8 #初始小区间划分的个数
a=np.loadtxt("Pdata4_20.txt")
a=a.flatten(); mu=a.mean(); s=a.std()
print("均值为：", mu); print("标准差为：", s)
print("最大值为：",a.max()); print("最小值为：",a.min())
bins=np.array([14.2, 14.625, 14.8375, 15.05, 15.2625, 15.475, 15.9])
h=plt.hist(a,bins)
f=h[0]; x=h[1] #提取各个小区间的频数和小区间端点的取值
print("各区间的频数为：",f,"\n小区间端点值为：",x)
p=ss.norm.cdf(x, mu, s)  #计算各个分点分布函数的取值
dp=np.diff(p)  #计算各小区间取值的理论概率
dp[0]=ss.norm.cdf(x[1],mu,s)  #修改第一个区间的概率值
dp[-1]=1-ss.norm.cdf(x[-2],mu,s)  #修改最后一个区间的概率值
print("各小区取值的理论概率为：",dp)
st=sum(f**2/(n*dp))-n  #计算卡方统计量的值
bd=ss.chi2.ppf(0.95,k-5) #计算上alpha分位数
print("统计量为：{}，临界值为：{}".format(st,bd))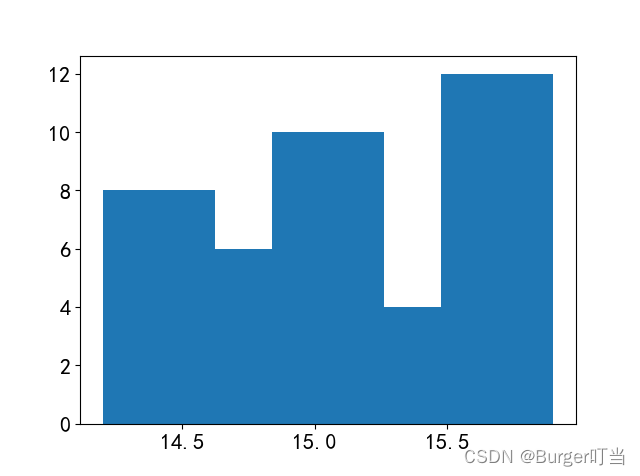

2. Kolmogorov-Smirnov检验

定义：Kolmogorov-Smirnov检验统计量

例4.21（续例4.6）检验学生的体重是否服从正态分布

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ss
a=np.loadtxt("Pdata4_6_2.txt")
w=a[:,1::2]; w=w.flatten()
mu=w.mean(); s=w.std(ddof=1)  #计算样本均值和标准差
print("均值和标准差分别为：", (mu, s))
statVal, pVal=ss.kstest(w,'norm',(mu,s))
print("统计量和P值分别为：", [statVal, pVal])

4.4 方差分析

4.4.1 单因素方差分析及python实现

*单因素方差分析：在一项实验中只考虑一个因素A的变化

例4.22 用4种工艺A1, A2, A3,A4 生产灯泡,从各种工艺制成的灯泡中各抽出了若干个测量其寿命,结果如表4.10所示，试推断这几种工艺制成的灯泡寿命是否有显著差异.

讲解见P151——P155

import numpy as np
import statsmodels.api as sm
y=np.array([1620, 1670, 1700, 1750, 1800, 1580, 1600, 1640, 1720,
            1460, 1540, 1620, 1680, 1500, 1550, 1610])
x=np.hstack([np.ones(5), np.full(4,2), np.full(4,3), np.full(3,4)])
d= {'x':x,'y':y}   #构造字典
model = sm.formula.ols("y~C(x)",d).fit()   #构建模型
anovat = sm.stats.anova_lm(model)  #进行单因素方差分析
print(anovat)

PR=0.042004<0.05，所以这几种工艺制成的灯泡寿命有显著差异

例4.23（均衡数据）为考察5名工人的劳动生产率是否相同，记录了每人4天的产量，判断他们的生产率有无明显差别。

import numpy as np
import pandas as pd
import statsmodels.api as sm
df = pd.read_excel("Pdata4_23.xlsx", header=None)
a=df.values.T.flatten()
print(a)
b=np.arange(1,6)
x=np.tile(b,(4,1)).T.flatten()
print(x)
d={'x':x,'y':a} #构造求解需要的字典
model = sm.formula.ols("y~C(x)",d).fit()  #构建模型
anovat = sm.stats.anova_lm(model)  #进行单因素方差分析
print(anovat)