剑指 Offer 14- II. 剪绳子 II——java

原创已于 2023-02-23 15:17:00 修改 · 225 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法

于 2022-07-14 19:59:18 首次发布

算法题专栏收录该内容

7 篇文章

订阅专栏

博客讨论了在解决绳子切割以获得最大乘积的问题时，如何运用推论和快速幂取余算法。文章指出，将绳子等分为长度3的段能最大化乘积，并解释了为何幂指数需要从n/3-1开始，以避免计算错误。同时，提供了Java代码实现来解决大数越界问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这一题最开始写的时候就懵懵的，看了解析以为懂了，今天再写又不会了，重新写一下思路。还是参考大佬的解析。
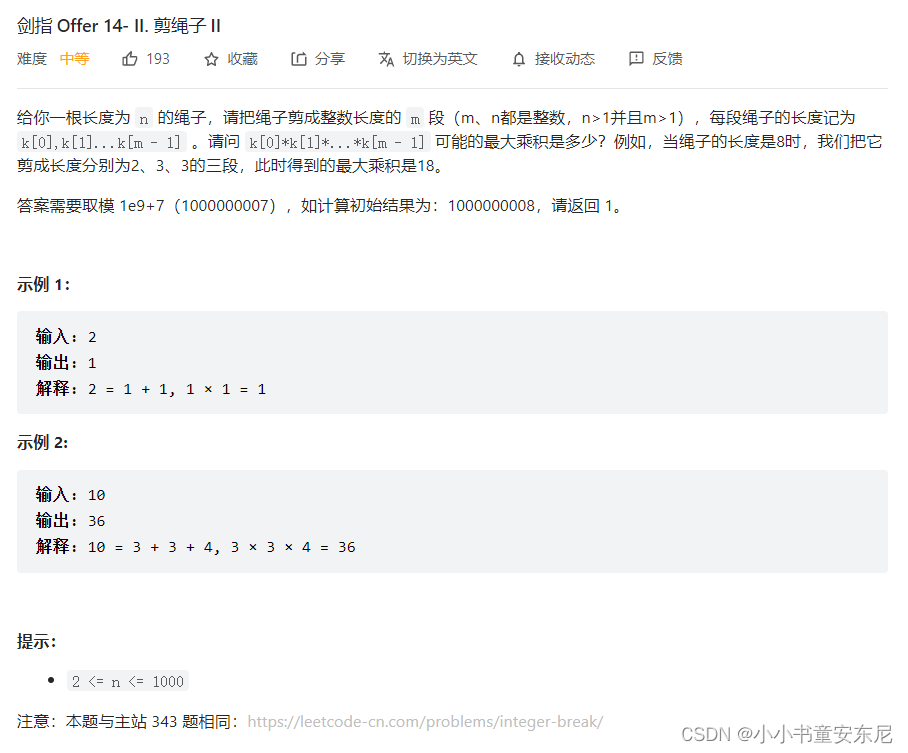
在这里插入图片描述

题目描述

在这里插入图片描述

思路

推论一：将绳子以相等的长度等分为多段，得到的乘积最大。
推论二：尽可能将绳子以长度 3 等分为多段时，乘积最大。
在这里插入图片描述

如果数字不大，根据推论和切分规则就能直接求结果，但是本题涉及大数越界情况下的求余问题，如2^1000 % 100000，它在运算途中就越界了，因此要再加上采取快速幂求余算法。
从快速幂取余算法思路详解可以得到此算法公式

在这里插入图片描述
困惑我的是为什么幂指数要从n/3-1开始，如果从n/3开始，如果余数为1，res/3*4%c的结果就不正确。
更新：原因在于：

题解

class Solution { 
    int c=1000000007;
    public int cuttingRope(int n) {
        if(n<=3) return n-1;
        int p=n%3;
        long res = 1;
        long a = 3; 
        int b=n/3-1;
        while(b > 0){
            if (b%2 ==1) res = (res*a)%c;
            a = (a*a)%c;
            b/=2;
        }
        if(p==0) return (int)(res*3%c);
        else if(p==1) return (int)(res*4%c);
        else return (int)(res*6%c);
    }
}