DCF的标准公式使用循环相关，这允许通过快速傅立叶变换(FFT)有效地实现学习。然而，FFT要求滤波器和搜索区域大小相等，这限制了检测范围。由于循环移位特性，滤波器在包含不现实的、环绕循环移位的目标的许多模板山被训练。减少开窗问题的一种简单方法是从更大的区域学习滤波器。然而，由于该区域中的大面积背景，DCF的跟踪性能显著下降。
本文提出了一种空间可靠性与通道可靠性去解决上述问题，如图所示：
上面一行对应空间可靠性，下面一行对应通道可靠性。空间可靠性利用了一个mask矩阵从而可以实现搜索区域的任意大小，并且文中还采用了图像分割的思想将不规则目标的特征提取出来。
通道可靠性引入了一个通道权重矩阵W（每个特征通道的辨别能力的缩放因子），并且在定位阶段运用于计算相关响应，这个权重矩阵可以有效降低加权平均滤波器响应的噪声。
下面我们先介绍如何求M和W：
求解mask矩阵：
这里引入了一个全概率公式：
注意：这里涉及到了很多概率论的知识，不了解的话可以参考这篇文章：
其中
是一个观察值，表示的是在训练区域第i个像素的颜色
和位置
c表示前景/背景的颜色直方图c = {cf，cb}。mi ∈ {0，1}是表示未知前景/背景标签的随机变量。（我认为这里的m跟掩码的原理差不多，目标出为1，背景处为0）
我们可以根据这张图理解这个公式
是一个先验概率，由前景/背景直方图提取的区域大小之间的比率来定义。
表示搜索区域的位置的概率，也可以叫做空间可能性，靠近目标中间的部分概率大，其他概率很小，对应与第二副图。由于远离中心的像素同样可能属于对象或背景，所以作者利用一个Epanechnikov核函数进行中心位置的加强。
表示的是外观可能性，通过贝叶斯规则从对象前景/背景颜色模型cf和cb中计算得到。对应与第三幅图。
与相乘就会得到第四张图，这里用到了马尔可夫随机场正则化（MRF），然后将其二值化后（mask矩阵）再作用域第一幅图（目标区域），就会得到最后一幅图，这里用到了图像分割的思想，并没有直接采用目标区域的矩形框，而是利用的目标的不规则区域作为特征提取。
求解通道权重矩阵W：
信道可靠性w反映了每个信道在目标定位阶段的重要性。它包括两种类型的可靠性度量:(I)在滤波器学习阶段计算的信道学习可靠性
，(ii)在目标定位阶段计算的信道检测可靠性
。
联合信道可靠性
被计算为两个可靠性度量的乘积：
信道学习可靠性的直接测量是学习信道滤波器的最大响应值，计算如下：
信道检测可靠性为：
表示的是基于通道响应中第二个和第一个最高非相邻峰值之比，这两个最大峰值是在3×3非最大值抑制后获得的两个最大值。该比率不利于多个相似物体出现在目标附近的情况，所以为了解决这种情况，不允许最终值低于0.5。
学习阶段：
传统DCF的目标函数为：
它是将各个通道的响应求和，再与期望输出求二范数，这样会导致一些通道可能会抑制其他通道一个数量级，如下图所示：
本文为了消除这种问题，独立考虑每个通道，其目标函数如下：
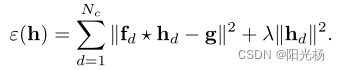
利用ADMM迭代法对这个目标函数进行优化，利用
这个等式约束构造拉格朗日乘子：ADMM解法
相当于
，m是上面所求的mask矩阵。
迭代子公式为：
求解得：
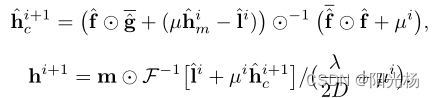
具体的推导在论文的附录部分。
算法流程如下：
求相关响应得分（定位阶段）：
为上述所求的通道权重矩阵。可以被认为是基于每个特征通道的辨别能力的缩放因子。
前景和背景直方图c被提取并通过具有学习速率ηc的指数平均衰减来更新。前景直方图由估计的对象边界框内的Epanechnikov核提取，背景从两倍于对象大小的邻域中提取。
特征是从在前一帧中以目标估计位置为中心的搜索区域中提取的，并与学习滤波器
相关联。通过对信道可靠性分数
加权的相关响应求和来定位目标。每个通道滤波器响应用于计算相应的检测可靠性值
扫一扫
9268
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
