计算机图形学实验六-多边形的Sutherland-Hodgman裁减算法

• 实验内容、目的、及要求

实验内容	多边形的Sutherland-Hodgman裁减算法；
实验目的	掌握相关算法的原理及实现
实验要求	实现基础代码； 图形化交互；

• 实验数据/结果，实验总结/收获

3.1 实验数据和结果

1. Sutherland-Hodgman裁减算法说明与测试

①算法说明

1. 基本思想

算法流程类似于流水线，即前边的结果是后边的输入。算法的每一次输出（包括中间结果）都是一个多边形的顶点表（逆时针排列），且所有顶点均位于相应窗口裁剪边额可见一侧。

裁剪边所在直线将平面分为两部分：可见一侧和不可见一侧，后面的讨论都是针对这两部分来进行点的取舍和计算的。

1. 算法概述

假设S、P为多边形的两个相邻顶点：S为边的起点、P为边的终点，则边SP与裁剪边之间只有4种可能的关系。

1. 图1显示的SP线完全可见（完全处于可见一侧），则输出P点，不需输出S点，因为顶点是按照顺序处理的，S作为前一边的终点输出的。
2. 图2显示的SP线完全不可见（完全位于不可见一侧），则无输出。
3. 图3显示的SP线部分可见（其中起点S在可见一侧，终点P在不可见一侧），此时输出SP与裁剪边交点作为新的终点P1。
4. 图4显示的SP线部分可见（其中起点S在不可见一侧，终点P在可见一侧），此时输出SP与裁剪边的交点作为新的起点S1，输出点P作为终点。

②算法设计

根据上文分析的四种情况，进行算法的设计，首先定义两个表：输入顶点表pIn（用于存放被裁剪多边形的顶点）、输出顶点表pOut（用于存放裁剪过程中以及结果的顶点），输入顶点表在初始化图形的时候将用户输入的顶点坐标加入其中，输出顶点表在裁剪过程中将裁剪后的输出点加入。

为了操作方便，我把常用的功能封装成函数进行调用，有以下几个子函数，判断顶点是否在裁剪窗口内的Inside函数，针对每个裁剪窗口边对每个顶点均判断一遍，当顶点在窗口内时返回true，反之返回false并break出switch判断体；判断多边形的边是否穿过裁剪窗口的Cross函数，若多边形的一条边的两个顶点均在裁剪窗口外或者均在裁剪窗口内，则未穿过裁剪窗口，返回false，反之，多边形的一条边的两个顶点一个在可见一侧，一个在不可见一侧，则为穿过裁剪窗口的情况，此时返回true；返回多边形边的裁剪矩形所在直线的交点的Intersect函数，针对每个裁剪窗口的边分情况求交点并返回，作为裁剪多边形后的顶点，此时的顶点应当存入输出顶点表中。

接下来就是实现核心功能-进行多边形的裁剪，将上面封装的子函数进行调用，结合算法说明中的四种情况，对不同的情况作不同的输出，这里主要为更新输入顶点表、输出顶点表，因为后面会有针对输入输出顶点表绘制多边形的函数（在补充说明中具体解释），所以至此多边形的裁剪算法已实现，调用相应的绘图函数，即可实现多边形的更新（裁剪后的多边形）。

整个算法流程的实现，包括初始化输入顶点表，如图1所示，多边形的裁剪，即更新输出顶点表，如图3所示，重新绘制裁剪后的多边形，如图2所示。

③算法测试

上图是针对凸多边形的测试，图1是初始化的矩形窗口和初始化的三角形，图2是利用多边形裁剪算法裁剪的多边形，改用红色的线进行绘制。

上图是针对凹多边形的测试，图1是初始化的矩形窗口和初始化的凹多边形，图2是利用多边形裁剪算法裁剪的多边形，改用红色的线进行绘制。

1. 鼠标交互与键盘交互说明与测试

鼠标交互说明：鼠标的交互体现在以下几个方面，一是初始化绘图窗口后，用户可以用鼠标左键点击的形式选择绘制点，根据用户输入的多边形顶点数循环点击依次存入顶点坐标，如图1所示；二是鼠标右键点击弹出菜单窗口（菜单窗口在补充部分具体说明），用于选择不同的操作，如图2所示；三是鼠标点击可以改变裁剪窗口的位置（在补充部分具体说明），如图3所示；四是鼠标滑轮滚动可以进行矩形框的缩放（在补充部分具体说明）。

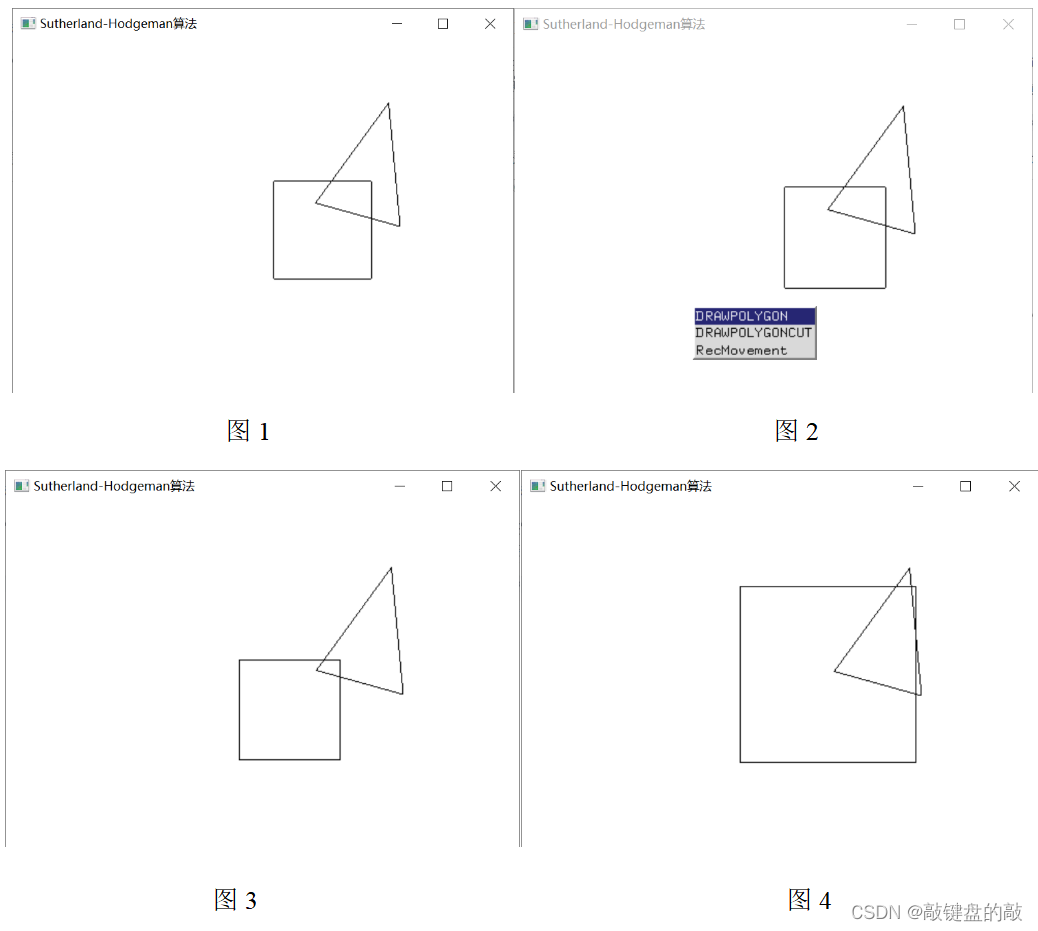
键盘交互说明：一开始的多边形顶点、裁剪矩形窗口的左下角和右上角顶点由用户利用键盘进行输入，多边形的顶点坐标可以由鼠标点击也可以用户手动输入。由于用户在鼠标点击之后不能改变多边形的形状，这里加入键盘交互，当用户按下0时，清空顶点数组，用户可重新进行鼠标点击选择顶点坐标进行绘制。

鼠标键盘交互的其他说明：这里绘制多边形，顶点的输入有两种形式，一个是鼠标点击，一个是用户手动输入，因为这里选择的OpenGL 中的模型视图矩阵堆栈是GL_MODELVIEW，这样相当于设置坐标轴位于画布中间，但是用户鼠标点击的时候，存入的顶点根据输出验证可以看出均为正值，说明这里用户用鼠标点击绘制的图像只能位于第一象限，若想让图像均匀分布在画布上，或者用户想精准绘制多边形，则可选用键盘输入的选项，若用户只是想快速绘制多边形，观察裁剪效果，则可以选择鼠标点击绘制多边形，若绘制结果不理想，可以按下键盘上的0键，重新绘制。

1. 其他补充说明

①多边形说明

这里绘制多边形，如下图所示，图1为绘制多边形的函数，将用户输入或者鼠标点击的顶点坐标存入动态数组xy和xyTmp中，因为后面的裁剪操作会覆盖xy的值，也就是会覆盖用户初始输入的顶点坐标，这里加入一个相同的动态数组xyTmp用于保存初始多边形顶点，具体代码如图2所示。

②矩形说明

主要说明的是矩形的绘制和矩形窗口的移动，关于矩形的绘制问题，因为在用户操作的时候可能要多次初始化矩形窗口，或者由于某些必要的操作会导致矩形窗口无法显示在画布上，此时就需要调用绘制矩形函数，重新在画布上显示矩形裁剪窗口，具体函数如图1所示。

关于矩形窗口的移动问题，由于一开始用户的输入已经确定的矩形裁剪窗口的大小和位置，所以我这里利用之前实验做过的图形平移和缩放操作改变矩形裁剪框的大小和位置，关于矩形框的平移操作：借助鼠标点击的位置，对矩形坐标进行修改，但是这里有个小小的bug，因为我是根据用户点击的点的位置进行矩形框位置的改变的，前面说道过，用户鼠标点击之后的坐标只能为正值，我考虑到一般用户设置的矩形框会偏右上，所以我利用简单的减法实现矩形框的左下方的平移，具体实现如图2所示。

关于矩形框的缩放操作，我借助鼠标滚轮的滚动实现矩形框的缩放，矩形实现是当检测到鼠标滚轮向前滑动时，为矩形的放大操作，我这里设置了0.01的缩放比例，可以更加细微的调节和观察矩形框的缩放情况，具体实现如图3、4所示。

详细代码见链接：https://download.youkuaiyun.com/download/weixin_53249260/88236656