最小生成树的创建（Prime普利姆算法、java实现）

bueee

已于 2022-03-05 20:39:39 修改

阅读量2.1k

点赞数 6

分类专栏：学习非日记文章标签：算法 java 图论二叉树数据结构

于 2021-12-22 10:54:24 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_52939031/article/details/122069495

版权

文章目录

前言
一、什么是最小生成树？
二、Prime算法简述
- 1.文字描述
- 2.图文演示
三、代码实现

前言

要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，我们可以选择将n个城市当成n个节点，然后将所有的节点相连接形成一个连通图，边上的数字代表与边相邻的两座城市之间铺设光纤的费用（权），但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

下面我们就将 A B C D E F G五座城市形成的带权连通图通过prim算法转换成最小生成树。

图1 五个城市形成的带权连通图,两个节点边上的数字代表铺设光纤的费用（权），没有表面数字的边表示与这条边关联的两个城市之间无法直接相通。
在这里插入图片描述

提示：以下是本篇文章正文内容，下面案例可供参考

一、什么是最小生成树？

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得
在这里插入图片描述

** w(T) 最小，则此 T 为 G 的最小生成树。**

例如图1 (A,B)代表连接顶点A与顶点B的边 w(A,B) = 5
规定T为无循环图是因为书的

最小生成树其实是最小权重生成树的简称。

二、Prime算法简述

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点（英语：Vertex (graph theory)），且其所有边的权值之和亦为最小。

1.文字描述

1).输入：一个加权连通图，其中顶点集合为V，边集合为E；
图1中
顶点集合V = {A.B,C,D,E,F,G}
边集合E = {（A,B),(B,D),(D,F),(F,E),(E,C),(C,A),(A,G),(B,G),(F,G),(E,G)}

2).初始化：Vnew= {x}，其中x为集合V中的任一节点（起始点），Enew= {},为空；
这里以A节点为起始点
Vnew = {A}

3).重复下列操作，直到Vnew= V：
相等的意思是原顶点V集合的全部节点经过下面你的操作全部加入到了新的节点集合Vnew中，这样每个节点找到的与之相连的节点形成的边满足权值最小。

a.在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且
v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

第一步：刚开始集合Vnew中只有一个节点A，现在我们要做的是，在V集合中寻找除了A节点以外的其他与A直接连接的节点（除A以外是因为节点A已经存在与Vnew集合之中），满足条件的节点有节点B,C,G。现在我们要对节点A与这三个节点形成的边的权值进行判断，选出权值最小的。w(A,C) = 7,w(A,G) = 2, w(A,B) = 5 显而易见，其中G节点与A节点形成的边的权值最小。

第二步：现在集合Vnew = {A,G}，在集合V中除了A，G节点意外直接与这两个节点相连接的节点有B,C,E,B,F。 w(A,C) = 7,w(A,B) = 5,w(G,E) = 4,w(G,F) = 6,w(G,B) = 3,能够看出G节点与B节点形成的边权值最小。

第三步：现在集合Vnew = {A,G,B},满足条件的节点有C,E,F,D。w(A,C) = 7,w(G,E) = 4, w(G,F) = 6,w(B,D) = 9,这里G节点与E节点形成的边的权值最小。

第四步：现在集合Vnew = {A,G,B,E} , w(E,F) = 5 通过判断 E节点与F节点形成的边的权值最小。

第五步：集合Vnew = {A,G,B,E,F), w(F,D) = 4 最小

第六步：集合Vnew = {A,G,B,E,F,D), w(A,C) = 7 最小

b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；

第一步：将G节点加入到集合Vnew中，w(A,G)边加入到集合Enew中

第二步：将B节点加入到集合Vnew中，w(G,B)边加入到集合Enew中

第三步：将E节点添加到集合Vnew中，w(G,E)边加入到集合Enew中

第四步：将F节点添加到集合Vnew中，w(E,F)边加入到集合Enew中

第五步：将D节点添加到集合Vnew中，w(F,D)边加入到集合Enew中

第六步：将A节点添加到集合Vnew中，w(A,C)边加入到集合Enew中
到目前为止：
Vnew = {A,G,B,E,F,D,A}
Enew = {(A,G),(G,B),(G,E),(E,F),(F,D),(F,D),(A,C)}

2.图文演示

第一步：刚开始集合Vnew中只有一个节点A，

现在我们要做的是，在V集合中寻找除了A节点以外的其他与A直接连接的节点（除A以外是因为节点A已经存在与Vnew集合之中），
满足条件的节点有节点B,C,G。
在这里插入图片描述

现在我们要对节点A与这三个节点形成的边的权值进行判断，选出权值最小的。w(A,C) = 7,w(A,G) = 2, w(A,B) = 5
显而易见，其中G节点与A节点形成的边的权值最小。

第二步：现在集合Vnew = {A,G}，

在集合V中除了A，G节点意外直接与这两个节点相连接的节点有B,C,E,F。
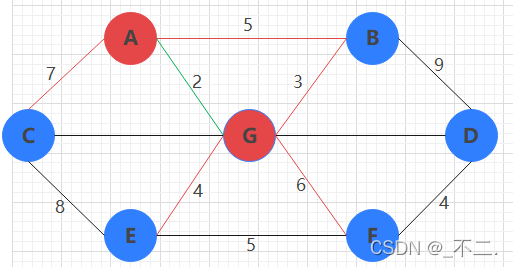
在这里插入图片描述

w(A,C) = 7,w(A,B) = 5,w(G,E) = 4,w(G,F) = 6,w(G,B) = 3,
能够看出G节点与B节点形成的边权值最小。

第三步：现在集合Vnew = {A,G,B},

满足条件的节点有C,E,F,D。
在这里插入图片描述

w(A,C) = 7,w(G,E) = 4, w(G,F) = 6,w(B,D) = 9,这里G节点与E节点形成的边的权值最小。

第四步：现在集合Vnew = {A,G,B,E} ,
满足条件的节点有C,D,F
在这里插入图片描述

w(E,F) = 5 通过判断 E节点与F节点形成的边的权值最小。

第五步：集合Vnew = {A,G,B,E,F),
满足条件的节点有C,D
在这里插入图片描述
w(F,D) = 4 最小

第六步：集合Vnew = {A,G,B,E,F,D),
满足条件的节点有C
在这里插入图片描述
w(A,C) = 7 最小

第七步：
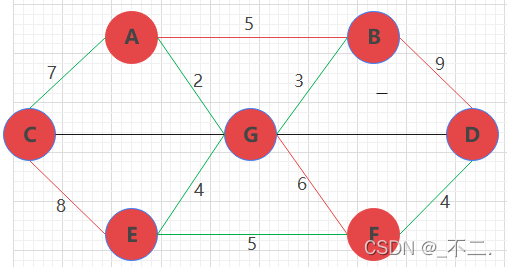
在这里插入图片描述
通过上述步骤我们得到的Enew集合中含有六条边分别是(A,C),(A,G),(G,B),(G,E),(E,F),(F,D)

形成的最小二叉树如下图
在这里插入图片描述
整理过后如下

三、代码实现

1.节点代码

class MGraph {
   
    int nodes; //节点的个数
    char[] element; //节点的元素
    int[][] side; //存放边，邻接矩阵

    public MGraph(int nodes) {
    //构造器
        this.nodes = nodes;
        element = new char[nodes];
        side = new int[nodes][nodes];
    }
}

2.邻接矩阵

我们通过邻接矩阵来实现各个城市之间的连通图

int[][] side = {
   
                {
   10000, 5, 7, 10000

最低0.47元/天解锁文章