一、简介
微分方程的经典数值方法有Ritz法、加权余量法、有限元法、有限体积法等等。对于微分方程的边值问题,如果能找到与微分方程相对应的泛函,可以通过求取相应泛函的极小值,将微分方程转化为关于基函数待定系数的代数方程。典型的近似方法如Ritz法。然而,流体力学中的方程通常是非线性的,难以找到泛函,此时可以使用加权余量法。
研究微分方程(在区域D内),满足边界条件
(在边界S上),其中L和B为微分算子。取微分方程的近似解
,要求基函数的选取满足边界条件。由于近似解u仅位于基函数所张成的空间内,如果精确解不落在此空间里,近似解u就不一定满足微分方程。因此,将u代入微分方程,会得到余量
。
虽然余量R(x)无法精确取到0,但可以做到的是,令余量的加权积分等于0。选择n个权函数Wi(i=1,2,…,n),就得到以a1,a2,…,an为未知量的代数方程组:
(i=1,2,…,n)
上式可以整理成为关于的线性方程组
的形式:
二、伽辽金法(Galerkin法)、最小二乘法和矩法
权函数的不同选取,代表了不同的误差分配,产生了不同的加权余量法。最简单的是配置法(在区域内选取n个点,在这些点上使得余量取到0);而本文重点关注矩法、最小二乘法、伽辽金法(Galerkin法)这三种方法,其权函数如下:
1. 矩法
(i=1,2,…,n)。(
就是余量R的各次矩,所以称为矩法)
2. 最小二乘法
最小二乘的思想为:令取极小,得:
(i=1,2,…,n),即相当于:
(i=1,2,…,n)
3. 伽辽金法(Galerkin法)
三、具体案例及Python实现
以下面的二阶常微分方程边值问题为例:
近似解取为
1. 主体求解流程
from sympy import *
import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
x = symbols('x')
#基函数,注意是从φ1(j=1)开始!
def get_phai(j):
eq = 1-x
for k in range(j):
eq=eq*x
return eq
#得到第num_weight个权函数
def get_weight(num_weight,method):
if method == 1:#Galerkin法
eq = get_phai(num_weight) #用基函数
if method == 2:#最小二乘法
eq = diff(diff(get_phai(num_weight),x),x)+get_phai(num_weight) #用R对ai的偏导数
if method == 3:#矩法
eq=x**(num_weight-1)#x的(i-1)次方
return eq
#获得Ax=b方程组里第num_weight行、第num_aj列的系数
def get_coef(num_weight,num_aj,method):
eq1 = diff(diff(get_phai(num_aj),x),x)+get_phai(num_aj) #R里aj的系数
eq2=get_weight(num_weight,method) #权函数Wi(x)
return integrate(eq1*eq2,(x,0,1))
def get_b(num_weight,method):
eq1=x #R里不含aj的项
eq2=get_weight(num_weight,method) #权函数Wi(x)
return -integrate(eq1*eq2,(x,0,1))
#x0点的数值解
def num_sol(x0,n,res):
sum = 0
for i3 in range(n):
phai_x0=get_phai(i3+1).evalf(subs ={'x':x0})
sum = sum + phai_x0*res[i3]
return sum
#x0点的精确解(利用常微知识易解)
def accu_sol(x0):
return sin(x0)/sin(1) - x0
#主体求解流程
def Weighted_Residual(n,method):
A=np.zeros((n,n)) #待求解方程组的系数矩阵,第i行对应用权函数Wi积分,第j列对应a_j前面的系数
B=np.zeros(n) #待求解线性方程组的右端项
res=np.zeros(n) #解(即a1,a2……,an)
for i1 in range(n):
for j1 in range(n):
A[i1,j1] = get_coef(i1+1,j1+1,method)#数组从0开始存储,基函数和权函数从1开始编号
for i2 in range(n):
B[i2]=get_b(i2+1,method)
#解线性方程组得到近似解的系数
res=linalg.solve(A, B)
return res
2. 不同方法和不同n值的误差比较
三种方法的比较:
def error_methods_compare(n):
#计算误差
x_list = np.linspace(0,1,100)
error_list_Ga = []
error_list_Sq = []
error_list_Mo =[]
for x0 in x_list:
error_list_Ga.append(num_sol(x0,n,Weighted_Residual(n,1))-accu_sol(x0))
error_list_Sq.append(num_sol(x0,n,Weighted_Residual(n,2))-accu_sol(x0))
error_list_Mo.append(num_sol(x0,n,Weighted_Residual(n,3))-accu_sol(x0))
#绘图
plt.plot(x_list,error_list_Ga,x_list,error_list_Sq,x_list,error_list_Mo)
plt.legend(['Galerkin','Least Square','Moment'])
plt.show()
returnerror_methods_compare(4)
以n=4为例,可见这些算法都有不错的精度(1e-6的量级);
同时,Galerkin法的精度明显高于其他方法。
不同n值的比较
def error_n_compare(method):
#计算误差
n_list=[2,3,4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 16, 20, 30]
x_list = np.linspace(0,1,100)
error_n_list=[]
max_error_list=[]
for n in n_list:
print("n:",n)
res_temp = Weighted_Residual(n,method)
abs_error_list=[]
for x0 in x_list:
abs_error_list.append(abs(num_sol(x0,n,res_temp)-accu_sol(x0)))
error_n_list.append(abs_error_list)
max_error_list.append(max(abs_error_list))
#绘图
plt.plot(n_list,max_error_list)
plt.xlabel('n')
plt.ylabel('max_error')
plt.yscale("log")
plt.show()
plt.plot(x_list,error_n_list[0],x_list,error_n_list[7],x_list,error_n_list[14])
plt.xlabel('x')
plt.ylabel('error_abs')
plt.yscale("log")
plt.legend(['n=2','n=9','n=30'])
plt.show()
return
error_n_compare(1) #Galerkin法
这里y轴采取对数坐标,并使用误差的最大值作为比较的标准。
起初,误差随着n的增大而显著下降,在n=9左右达到最小误差;然而,随着n的进一步增大,误差反而有一定的回升,这说明并不是n越大越好。这可能是因为,n过大时,多项式基函数的阶数过高,解的振荡越来越严重,从而产生了类似龙格现象的问题。
下面观察不同n值时误差log值在(0,1)上的情况:

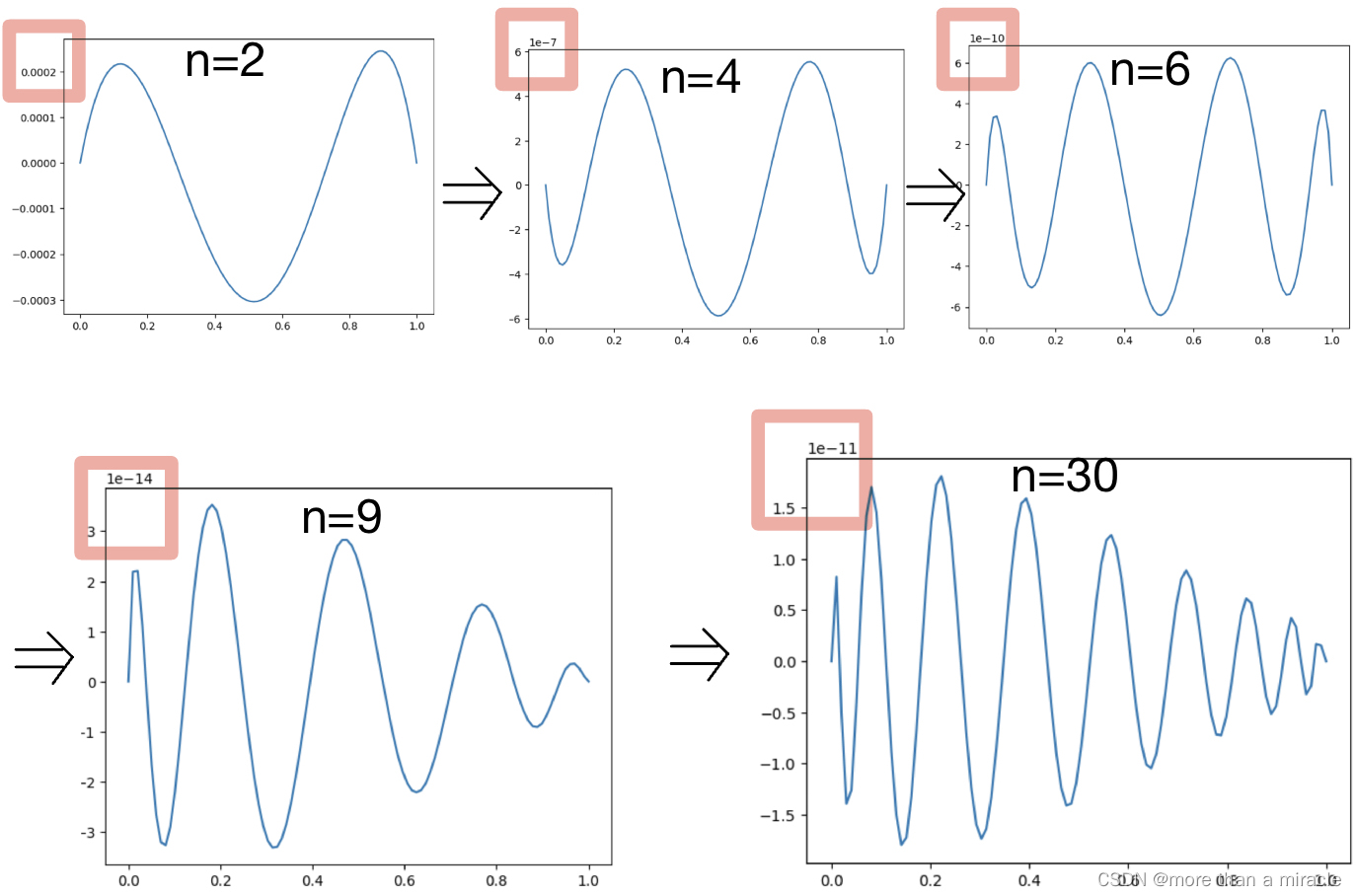
同样可以看到解的误差随n的变化趋势。n越大,多项式阶数越高,解的振荡越明显,n过大反而会导致更大的误差。
























 2517
2517

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








