- 本篇笔记为方便自己再次阅读而记录,包含了原文的(部分)翻译以及自己的理解。
- 原文内容十分丰富,本部分笔记仅摘取了核心的算法部分,对于介绍、综述、理论证明、一些细节以及扩展暂未纳入。
- 习惯用语和某些术语保持英文。(例:assortment、rollout)
- 本也是初次接触 revenue management 领域,理解尚不透彻,有任何错误恳请批评指正,有任何侵权或者不妥之处请及时告知,将第一时间处理。
Dynamic Assortment Optimization for Reusable Products with Random Usage Durations
Rusmevichientong, Sumida, and Topaloglu
摘要
本文考虑reusable products的dynamic assortment optimization问题,其中每个到达的顾客在公司提供的assortment里选择一个产品(或离开),使用一段随机长度的时间,然后将产品归还给公司供其他顾客再次使用。我们的目标是找到一个策略来决定提供给每个顾客的assortment,以最大化在一个有限长销售季内的总期望收益。
问题的动态规划表述需要一个高维状态变量,来记录on-hand产品库存以及已被使用不同时长的产品数量。本文提出了一种易处理的方法,来计算出一个能从理论上保证获得最优总期望收益至少50%的策略。该策略基于对最优值函数构建的线性近似。
当使用时长无限或者服从负二项分布时,本文也提出了在简单静态策略上执行 rollout 的高效的方法。执行rollout对应的是对值函数的可分的、非线性的近似。同样地,相应的策略也能保证获得最优总期望收益的至少50%。
文中模型的一种特殊情况是具有无限使用时长的情况,顾客直接购买产品而不再归还。这种情况下,本文提出了一种改进的 rollout 方法,可以保证至少获得最优总期望收益的的比例,其中 Cmin 是产品库存的最小值,R 是产品价格在销售季内的最大相对离差。
本文基于模拟的数据以及西雅图市的实际停车交易数据进行了dynamic assortment management的计算实验。计算实验表明,提出的策略在实际表现上明显优于其理论性能保证,并且执行 rollout 可以带来明显的改进效果。
2. 问题表述(注:采用的是原文的编号)
sequence of events
2.1 Problem Data
:n 种产品
:产品 i 的初始库存量
:销售季内的T个时间周期。每个时间周期对应一小段时间间隔,假设每期正好有且仅有一个顾客到达。(不难扩展到每期至多有一个顾客到达的情况,并将时间间隔取得足够小)
:产品集的一个子集(assortment)
:Feasible assortments的集合(允许了对于assortment的约束)
:第 t 期到达的顾客在面临assortment S 的时候选择产品 i 的概率(
),由一个离散选择模型决定
:顾客在第 t 期开头决定租用产品 i 需要支付的one-time upfront fee
:顾客在第 t 期内使用产品 i 需要支付的per-period rental fee
:(随机变量)产品 i 的使用时长(假设不同单元的使用时长是彼此独立的)
:the hazard rate of rental duration
2.2 State and Transition Dynamics
状态和状态空间:
,其中
表示产品 i 的on-hand的单元数量,
表示产品 i (在某个周期开头时)已经被使用了 l 期的单元数量。
状态空间为:。我们假设系统的初始状态下所有的产品单元都是on-hand的,因此
,进而状态空间是有限维的。
状态转移方程:
(1)式表示的是,如果在第 t 期没有购买发生,那么第 t 期的状态 在第 t+1 期会转移到
。解释如下:根据定义
。考察产品 i 的已被使用 l 期的这些单元,每个单元在下一期开始之前被归还的概率都为
,且不同单元互相独立,因此这些单元里被归还的数量为二项分布随机变量
,叠加到下一期状态的
项;未被归还的数量为
,成为下一期状态的
项;而考察产品 i 的on-hand的单元,由于没有购买,它们在下一期保持on-hand,进入下一期状态的
项。
2.3 Dynamic-Programming Formulation
以及边界条件

其中,是参数为ρ的0-1随机变量;
是只有第(i,k)位的坐标为1,其余坐标都是0的向量(将状态
看成一个向量);
为状态-值函数,表示当系统在第 t 期开头处于状态
时,在时间周期 t,...T 上所能获得的最优总期望收益。通过求解(2)式的线性规划,可以得到最优值函数
。
解释:第 t 期开头时的最优总期望收益,等于在当前步骤做最优决策获得的当期收益加上 t+1 期以后的最优总期望收益。① 等式右边的第一项为当期收益中已有顾客的rental fee(与assortment无关);②考虑新到达顾客的选择行为,给定 assortment S 时,顾客购买产品 i 的条件是顾客从S中选定了产品 i 且产品 i 有 on-hand 库存,概率为 ;如果顾客购买产品 i ,可以获得
的当期收益,如果顾客不购买任何产品,则没有任何当期收益;③ 考虑 t+1 期的状态,如果没有发生购买,按(1)式定义,下一期状态为
,最优总期望收益为
;如果购买了产品 i,那么
(当期就归还)对应的下一期状态为
,
(下一期继续使用)对应的下一期状态为
,此时下期的最优总期望收益为
为了简化动态规划公式,注意到由于不同单元的使用时长是彼此独立的, 和
这两个随机变量也是彼此独立的,因此可以化简如下:
将该式代入(2)式的动态规划公式进行整理,即可得到如下的等价表达式
注意到
的含义是在第 t 期出售一单元产品 i 的边际价值(反之:机会成本)。
另外,值得注意的一点是,上式动态规划的决策中,并不需要对于提供的assortment施加显式的约束来确保assortment里不包含库存为0的产品。只需要对离散选择模型和决策可行集添加一些很弱的假设,就能保证最优策略永远不会提供零库存的产品。
假设 2.1
可替代性保证了,当assortment增加新的可选项时,选择原来某个产品的概率一定不会上升;第二个假设保证了从可行assortment中减少选项时,仍然满足可行性。
这样的假设就能保证最优策略永远不会提供零库存的产品。观察(3)式的最大化问题,产品 i 的贡献等于: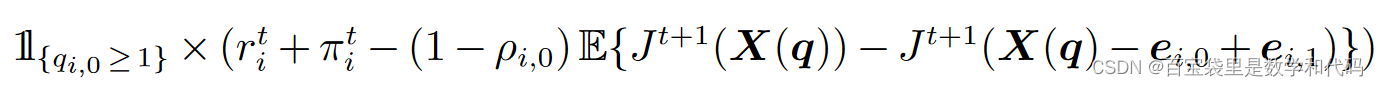 。我们总是可以把所有贡献非正的产品从S中移除,并保证最大化问题的目标函数值不会减小(可替代性保证了正贡献的产品的选择概率增大;可行性保证了移除后的assortment依然可行)。由于零库存产品的贡献等于0,因此自然地,最优策略永远不会提供零库存产品。
。我们总是可以把所有贡献非正的产品从S中移除,并保证最大化问题的目标函数值不会减小(可替代性保证了正贡献的产品的选择概率增大;可行性保证了移除后的assortment依然可行)。由于零库存产品的贡献等于0,因此自然地,最优策略永远不会提供零库存产品。
计算最优值函数的难点之一在于(3)式中的最大化问题是一个从集合中选择子集的组合优化问题。但是,在很多特定的离散选择模型下,已经存在一些有效的求解算法。这篇文章后续也会讨论主要的结果怎样扩展到只能近似求解这个组合优化问题的情况下。
找到最优策略的另一个难点是,我们需要为每一个 和
计算最优值函数
,状态空间的大小
随着 n 和 T 指数增长,这使得直接用(3)式进行动态规划的计算面临维度灾难问题。因此,文章接下来的关注点都是怎样提出计算高效的近似策略并取得可证明的性能。
3. 线性值函数近似
我们提出了一种构建最优值函数的线性近似的方法,并分析了一种利用该近似的策略的表现。具体地,我们给出了一个易处理的recursion 来得到线性值函数近似。我们证明了,如果使用基于该线性值函数近似的贪心策略,可以确保获得最优总期望收益的至少50%。
3.1 线性值函数近似的详细说明
(4)
其中 含义是第 t 期一单元已使用了 l 期的产品 i 的边际价值;
含义是第 t 期一单元on-hand的产品 i 的边际价值。我们recursively计算
如下:
- Initialization:设置
- Backward Recursion:对于
:令
满足
(5)
得到后,对于
:
(6)
直观意义的解释:
① 可以理解为线性值函数近似下第 t 期能提供的最理想的assortment(忽略库存可用性的情况下)。回忆动态规划的等价表述(3)式:

只要丢掉indicator function (忽略库存可用性),并将
替换为线性近似
,即可得到(5)式的最大化问题。
② 将(6)式改写为一种等价的形式:
衡量的是第 t 期一单元on-hand的产品 i 的边际价值。
对于这个产品单元,当我们提供了理想的assortment 时,顾客选择产品 i 的概率为
,而产品 i 有 Ci 单元的库存,因此我们关注的这个产品单元被顾客选择到的概率为
;
如果它被顾客选择,可以获得upfront fee以及该期的rental fee,然后接下来的价值取决于顾客在使用一期后是否归还:若归还(概率为 ),则该产品单元成为第 t+1 期的on-hand的产品 i 的单元,预估价值为
;若续租,则该产品单元成为第 t+1 期的已使用一期的产品 i 的单眼,预估价值为
;
如果它未被顾客选择,则本期内不获得任何收益,并成为第 t+1 期的on-hand的产品 i 的单元,预估价值为 。
同理,针对 对应的产品单元在下一期是否被归还的两种情况讨论,容易理解公式
3.2 一种利用边际价值的近似策略
我们考虑基于值函数近似 的贪心策略。如果系统在第 t 期处于状态
,那么该策略提供如下的assortment:

(7)
与计算线性值函数近似的(5)式相比,实际提供的贪心策略添加了 这一项:当产品 i 没有on-hand 库存时,提供产品 i 是无法获得后续收益的。在前文中也已经证明,这样的贪心策略保证了我们选择assortment时不会提供库存为0的产品。
尽管可以从理论上证明,这样的贪心策略可以获得最优总期望收益的至少50%。但这样的策略存在一个明显的问题:它在决策assortment时虽然考虑了系统状态,但只考虑产品 i 有库存与否,却根本不区分还剩下很多库存和只剩下少量库存的情况。因此,下面一节文章将提出一种将具体库存水平纳入考虑的策略,同时依旧保证获得最优总期望收益的至少50%。
4. 通过Rollout改善策略表现
为了得到一种显式地考虑产品库存水平的策略,我们从一种每个特定时间周期提供固定assortment的静态策略出发进行构建。根据(5)式中定义的assortment ,静态策略在第 t 期总是提供相同的assortment,不考虑此时的系统状态
。我们在静态策略上执行Rollout来获得一种考虑产品库存水平的策略,同时依然保持静态策略的性能的理论保证。利用静态策略对应的值函数是可以按产品分解的这一事实,我们证明,当使用时长服从负二项分布或者当顾客直接购买产品而不再归还的情况下,我们可以在静态策略上计算高效地执行Rollout。
4.1 静态策略的性质
我们考虑(5)中所定义的,在第 t 期总是提供assortment 的静态策略。当顾客选择了一个可用库存为0的产品时,他直接离开系统。下面的引理证明,这样的静态策略可以获得最优总期望收益的至少50%,证明类似于对基于线性值函数近似的贪心策略的分析,细节见附录D。
用 表示,静态策略下,当我们在第 t 期开头处于状态
时,经过时间周期 t,...,T 的总期望收益。类似于(3)式的动态规划,我们可以recursively计算
:
重新整理式子后得到:
以及边界条件。
下面说明 可以按产品分解。证明见附录E。

回忆(1)式可以发现, 只是
的函数,与其他产品无关。因此可以重新定义变量
引理 4.2 (Decomposability by Products)
其中对于每个
,
通过分别的 recursion 计算:
以及边界条件
4.2 基于静态策略的Rollout策略
关于Rollout算法基本思想的介绍可以参考该链接:【强化学习与最优控制】笔记(七) Rollout 与 Policy Improvement - 知乎如需教材电子版的同学可以从如下链接中获取: Dimitri P. Bertsekas 强化学习2021版教材和视频课程推荐上一期笔记,忘记的小伙伴可以复习一下: 王源:【强化学习与最优控制】笔记(六) 强化学习中的Decompositio… https://zhuanlan.zhihu.com/p/301537841 为了在静态策略上实施Rollout,我们提供这样的策略
https://zhuanlan.zhihu.com/p/301537841 为了在静态策略上实施Rollout,我们提供这样的策略 :最大化当前时间周期的即时期望收益(
和
),加上从下一个周期开始使用静态策略的总期望收益(
)。这个Rollout策略最终对应于使用
作为
的一种可分的非线性近似。
前两个等式运用了与(2)式和(3)式类似的动态规划的构建方法,唯一的区别是:最大化目标中,从下一周期开始的总期望收益由最优策略下的值函数,替换为了静态策略下的值函数。第三个等式是因为静态策略下的值函数可以按产品分解:
,因此
只剩下与产品 i 相关的部分。
众所周知,通过对基础策略实施Rollout获得的新策略具有策略改善的性质。因此,上述Rollout策略也可以获得最优总期望收益的至少50%。
5. 扩展
5.1 异质顾客类型
我们有m种顾客类型记为 。在第 t 期,到达的顾客类型为 j 的概率是
,其中
,因为每个时间周期有且仅有一位顾客到达。我们可以观察到每个到达顾客的类型。每个顾客类型有自己的选择模型、奖励结构、assortment 约束和使用时长。因此第2节中的模型进行了相应的扩展:
- 选择概率定义为
。(注意:如果我们观察不到每个到达顾客的类型,那么我们可以继续使用第2节中的模型,其中选择概率
是通过不同类型顾客对应的选择模型混合得到的)
- upfront fee 和 rental fee 定义为
和
- 相应的 hazard rate
- 提供给不同类型顾客的assortments 有不同的可行性要求,表示为
- 为了充分捕捉系统的状态,由于每个顾客类型有自己的奖励结构和使用时长,因此我们需要跟踪正在被每种类型顾客使用的单元数量,即:
。
- 使用
作为状态变量,我们可以给出类似(2)式中的动态规划公式。这种情况下,我们使用如下形式的值函数近似:
。其中
捕捉了第 t 期一单元on-hand的产品 i 的边际价值,而
捕捉了第 t 期一单元已经被顾客类型 j 使用了 l 期的产品 i 的边际价值。
与第3.1节中类似,recursively计算和
:
- Initialization:设置
- Backward Recursion:对于
:观察到顾客类型 j 后,令
满足:
得到后,利用第 t+1 期的估计值来倒推第 t 期,对于
:
(12)
(12)的第一式也可以化简为:
使用与前面两节相似的论述,我们可以证明基于线性值函数近似的贪心策略可以获得最优总期望收益的至少50%;同样可以对静态策略实施 rollout 来将产品的库存水平纳入考虑,同时也能保证获得最优总期望收益的至少50%。这两个结果都在附录G中详述。
另外,异质顾客类型的设定也可以用于建模使用时长在提供assortment前就可获知的情况(按使用时长来划分顾客类型)。
5.2 离散价格集下的定价优化
我们将模型扩展到对 upfront fees 和 rental fees进行决策,然后顾客基于价格进行选择。具体来说,我们为每种产品 i 创建了多个副本,不同的副本对应于不同的价格,每个副本称为一个虚拟产品。新的变量定义如下::每个产品的可能副本的集合。
表示所有虚拟产品的集合。
:产品 i 采取副本 h 对应的价格时,第 t 期的upfront fee
:产品 i 采取副本 h 对应的价格时,第 t 期的rental fee
仿照前面两节的思路,我们也可以得到有50%理论保证的策略,唯一的区别是:原来的产品集合 换成了虚拟产品集合
,我们每个周期从虚拟产品中选择一个assortment来最大化总的期望收益。需要注意的是,由于每次提供一种实际产品时只能有一个价格,即:在某个实际产品的所有虚拟副本中,我们最多只能提供一个。因此,assortment的可行集
6. 计算实验
下面进行计算实验来测试我们的策略的表现。在6.1节中,我们提出了一种方法来获得最优总期望收益的上界,它可以用来评估我们所提策略的最优性差距(optimality gap)。在6.2和6.3节中,我们给出计算结果。
6.1 最优总期望收益的上界
为了计算最优总期望收益的上界,我们提出了如下的线性规划模型,其中顾客的选择和状态转移动态(transition dynamics)都取期望值。
决策变量:
第t期提供assortment A的频率(frequency)
第t期(开头观察时)产品 i 被使用了正好 l 期的期望单位数
目标函数:整个销售期内的总期望收益
(1)第 t 期新出售的产品带来的收益:如果第 t 期我们提供assortment 的频率(frequency)为
,那么第 t 期顾客选择产品 i 的概率为
,因此第 t 期新出售产品带来的收益是
。
(2)第 t 期续租的产品带来的收益:第t期处于续租状态(in use)的产品 i 的期望单位数为,因此第 t 期续租的产品带来的收益是
。
约束:
约束1跟踪(keeps track of)使用了不同时长的产品的期望单位数
下面拆分成三部分进行解释:
① 给定顾客选择推导系统状态的变化——在第t期开头,系统状态为,如果这期到达的顾客购买产品 i ,那么下一期开头系统的状态就是随机变量
,其中
是以
为参数的0-1随机变量;而如果顾客不购买任何产品,那么下一期开头系统状态为
。
② 推导顾客选择的概率——如果第t期我们提供 assortment 的频率(frequency)为
,那么顾客购买产品 i 的概率为
综合上面两部分可知:
③ 利用 和
的独立性进行重新整理,代入
,化简可得上面的约束1的表达式
约束2对系统状态进行初始化
约束3确保我们每期都会提供assortment(但这个assortment也可以是空集)
可以观察发现,上述问题的目标函数和约束确实对于和
是线性的。注意到其中的
项,回忆(1)式:
 其中
其中,因此
对于
是线性的。
另外,如同第2节中所论述的,因为产品在一个销售期的最开始都是闲置在手上可用的,所以在上述线性规划的可行解中,因此决策变量和约束的数量都是有限的。
- 文章后续基于模拟的数据以及西雅图市的实际停车交易数据进行了dynamic assortment management的计算实验。结果表明,提出的策略在实际表现上明显优于其理论性能保证,并且执行 rollout 可以带来明显的改进效果。
- 本篇笔记仅给出计算实验的代码,更详细的分析将在后续笔记中继续讨论。
计算实验一的部分结果展示:
如图,这个setup下的关键在于,更加挑剔的顾客倾向于在更晚的周期到达,因此需要将未来的顾客到达情况纳入考虑,并小心地为他们保护库存。
Myopic Policy
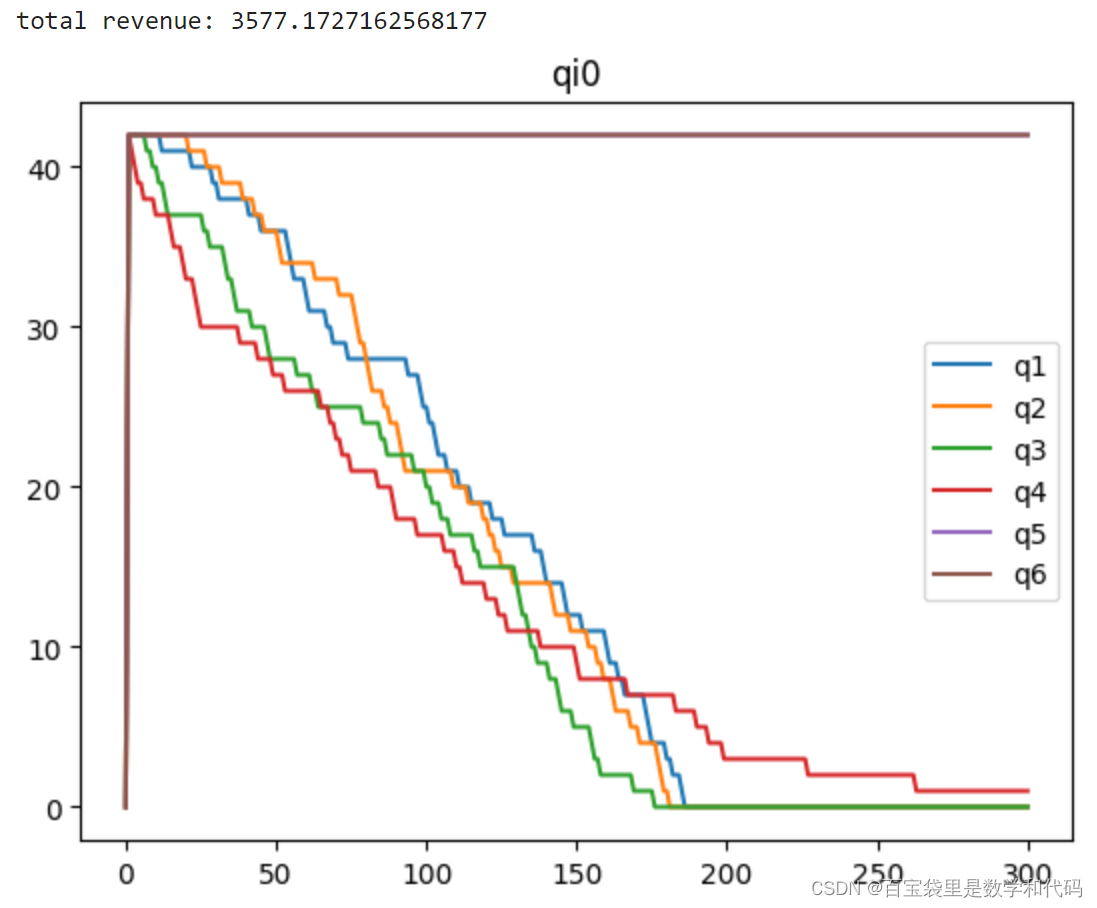

Greedy Policy


Rollout Policy










 本文研究了在不确定使用时长下的可重用产品动态优化问题,通过动态规划和线性近似方法,提出保证至少50%最优收益的策略。文章还介绍了rollout方法在无限使用时长或负二项分布情况下的应用,并通过实验展示了策略的优越性和rollout的改进效果。
本文研究了在不确定使用时长下的可重用产品动态优化问题,通过动态规划和线性近似方法,提出保证至少50%最优收益的策略。文章还介绍了rollout方法在无限使用时长或负二项分布情况下的应用,并通过实验展示了策略的优越性和rollout的改进效果。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








