（col x-y x+y 利用了数学斜线方程的x,y关系）（法二：位运算） n皇后问题 Leetcode81

思路

题目

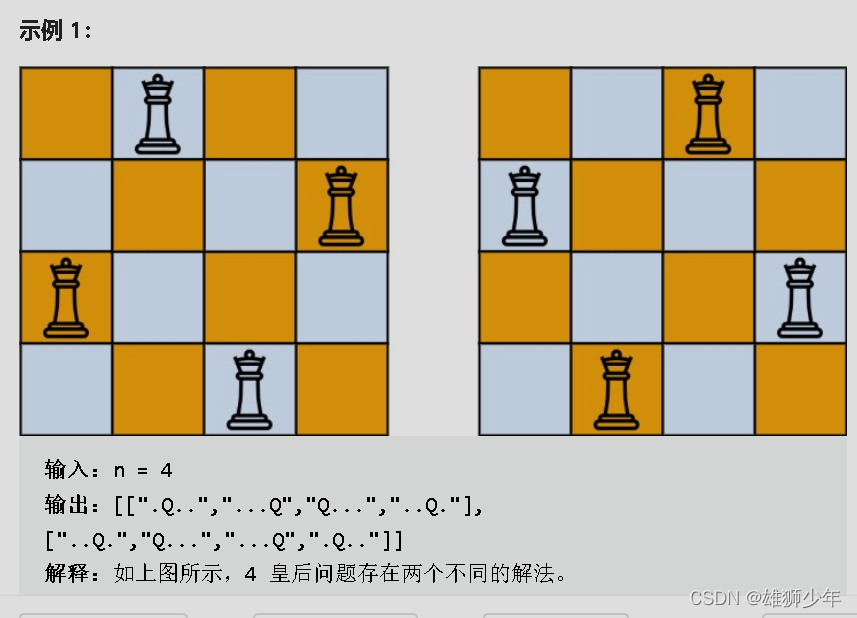
任意两个皇后不能在同一列， 也不能在正斜对角线 和 负斜对角线上

代码及注释

class Solution {


    List<List<String>> res ;
    Set<Integer> col;
    Set<Integer> xy_sub;
    Set<Integer> xy_sum;
    public List<List<String>> solveNQueens(int n) {
         res = new LinkedList<>();

        col = new HashSet<>();
       xy_sub = new HashSet<>();
       xy_sum = new HashSet<>();

         int[] path = new int[n];
        Arrays.fill(path,-1);
        dfs(n,path,0);
        return res;



    }


    public void dfs(int n , int[] path,int row){
        if(row == n){
          List<String> board =   Generat_List(path,n);
          res.add(board);
          return;
        }

        for(int i =0; i<n; i++){
            if(!col.contains(i) && !xy_sub.contains(row - i) & !xy_sum.contains(row + i)){
                path[row] = i;
                col.add(i);         // 你怎么忘记标记 “列” 了呢？
                xy_sub.add(row - i);
                xy_sum.add(row + i);
                dfs(n, path,row +1);

                path[row] = -1;  // 撤销影响
                col.remove(i);   // 不止工作数组要撤销影响，最主要的是标记数组要撤销影响啊
                xy_sub.remove(row - i);
                xy_sum.remove(row + i);
            }
        }
        
    }

    public List<String> Generat_List(int[] path,int n){
        List<String> board = new LinkedList<>();
        
        for(int p : path){
            char[] row = new char[n];
            Arrays.fill(row,'.');
            row[p] = 'Q';
            board.add(new String(row));
        }

        return board;
    }

}

n皇后问题II（简单，只需返回 有多少种布局）

class Solution {
    
    Set<Integer> col;
    Set<Integer> xy_sub;
    Set<Integer> xy_sum;
    int res_Sum = 0;
    public int  totalNQueens(int n) {
        col = new HashSet<>();
       xy_sub = new HashSet<>();
       xy_sum = new HashSet<>();



        dfs(n,0);
        return res_Sum;



    }


    public void dfs(int n ,int row){
        if(row == n){
            res_Sum++;
          return;
        }

        for(int i =0; i<n; i++){
            if(!col.contains(i) && !xy_sub.contains(row - i) & !xy_sum.contains(row + i)){
                col.add(i);         // 你怎么忘记标记 “列” 了呢？
                xy_sub.add(row - i);
                xy_sum.add(row + i);
                dfs(n, row +1);


                col.remove(i);   // 工作数组要撤销影响，最主要的是标记数组要撤销影响啊
                xy_sub.remove(row - i);
                xy_sum.remove(row + i);
            }
        }
        
    }


}

位运算解法（返回 有多少种不同的布局）

class Solution {

    int res_Sum = 0;
    public int  totalNQueens(int n) {
        int col = 0;
        int pie = 0;
        int na  = 0; // 初始时，从第0 行开始分配棋子， 此时棋盘上没有棋子，所以没有不能下的col、pie（左斜线）、（右斜线），所以 col等为0（其实参与运算时的形式是col=0000）
        dfs(n,0,col,pie,na);

        return res_Sum;

    }


    public void dfs(int n, int row, int col, int pie, int na){
        
        // 把所有 列 和 斜线 的位置都“或” 之后，再取反，这些位置就变成了0了，再与 n个1 “1111” 做“与运算”， 就可以的到当前能下的位置
       int  remain = ~(col | pie | na) & ((1 << n) - 1);

        if(row == n){
            res_Sum++;
            return;
        }

        while(remain != 0){

            int choice = remain & (-remain);    // 这里只是 每次都选最后面的一个没下过的
            remain = remain & (remain - 1);
            dfs(n,row+1, col | choice,  (pie | choice) << 1,  (na | choice) >> 1);
            // 这里不用撤销， 因为工作数组的变化都是在dfs函数参数列表里变化的
        }

    }


}
// @solution-sync:end

class Main {

    public static void main(String[] args) {
        int n = 4;

        int result = new Solution().totalNQueens(n);
        System.out.println(result);
    }

}