栈的存储结构与操作：顺序栈、链栈与后缀表达式转换-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_52001949/article/details/120297898

栈的顺序存储结构及实现

栈的顺序存储结构--出栈操作

栈（stack）：是限定仅在表尾进行插入和删除操作的线性表

栈顶（top)==允许插入和删除的一端；

另一端的称为栈底

先进先出的线性表。LIFO结构

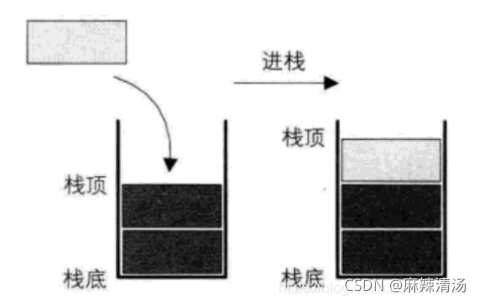
栈的插入操作，叫做进栈、压栈或入栈。（push）
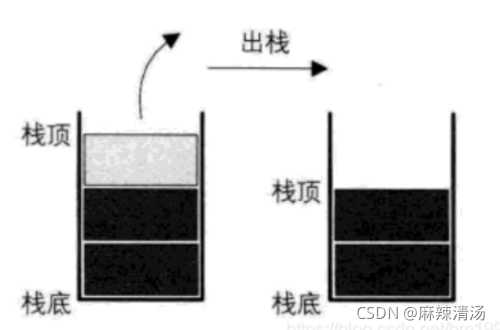
栈的删除操作，叫做出栈，也有的叫做弹栈。（pop）栈的顺序存储结构及实现

栈的顺序存储结构及实现

下标为0的一端作为栈底比较好

若有一个栈，StackSize是5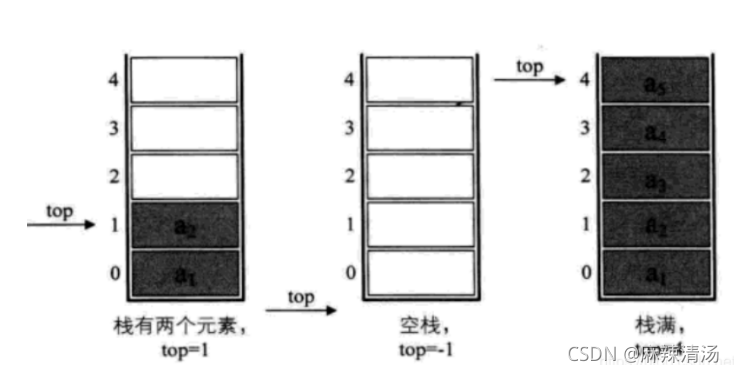

栈的插入，即进栈操作，其实就是做了如图所示的处理。


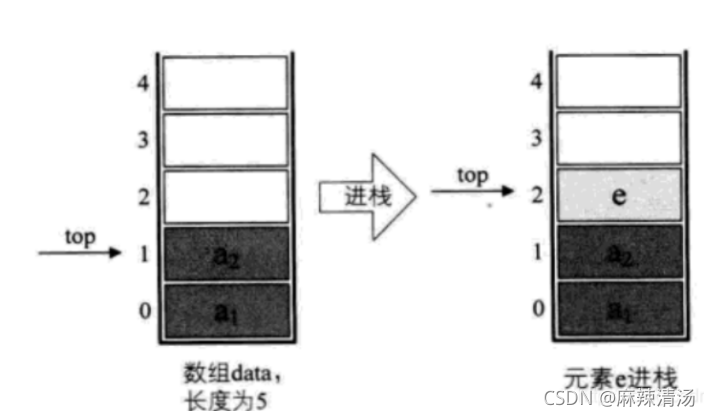
/*插入元素e作为新的栈顶元素*/
status Push(SqStack *s,SElemType e)
{
    if(S->top==MAXSIZE-1) //栈满
    {
        return ERROR;
    }
    S->top++;  //栈顶指针加一
    S->data[S->top]=e;  //将新插入的元素赋值给栈顶空间
    return OK;
}

栈的顺序存储结构--出栈操作

//若栈不空，则删除s的栈顶元素，用e返回其值，并返回OK，否则返回ERROR
Status Pop(SqStack *s，SElemType *e)
    if(s->top==-1) //栈空{
        return ERROR;
    }
    *e=S->data[s->top];  //将要删除的值赋给e
    s->top--;            //栈顶指针向下走
    return OK;
}

两者均没有涉及到任何循环语句，时间复杂度均是O(1)。

两栈共享空间

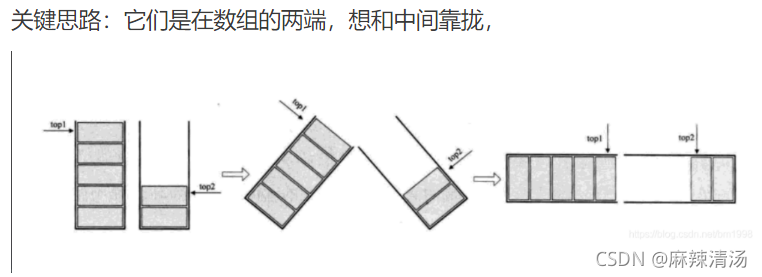
栈满：S->top1+1==S->top2

/*两栈共享空间结构*/
typedef struct
{
    SElmeType data[MAXSIZE]；
    int top1;
    int top2;
}SqDoubleStact;

对于两栈共享空间的push方法，我们除了要插入元素值参数外，还需要一个判断是栈1还是栈2的栈号参stackNumber。插入元素的代码如下；

/*插入元素e为新的栈顶元素*/
Status Push(SqDoubleStack *S , int e , int StackNumber)
{
    if(S->top1+1==S->top2)//栈已满，不能再push新元素了
    {
        return ERROR;
    }
    if(StackNumber==1)//栈1有元素进栈
    {
        S->data[++S->top1]=e; //若栈1则先top1+1后给数组元素赋值
    }
    if(StackNumber==2) //栈2有元素进栈
    {
        S->data[--S->top2]=e; //若栈2 则先top2后给数组元素赋值
    }
}

对于两栈共享空间的pop方法，参数就只是判断栈1栈2的参数stackNumber，代码如下；

Status Pop(SqDoubleStack *S,SElemType *e,int StackNumber)
{
    if(StackNumber==1)
    {
        if(S->top1==-1)
        {
            return ERROR;  //说明栈1已经是空栈，溢出
        }
        *e=S->data[S->top1--]; //先把删除的数据赋值，在减一
    }
    else if(StackNumber==2)
    {
        if(S->top2==MAXSIZE)
        {
            return ERROR; //说明栈2已经是空栈，溢出
        }
        *e=S->data[S->top2++] //栈2的栈顶元素
    }
    return OK;
}

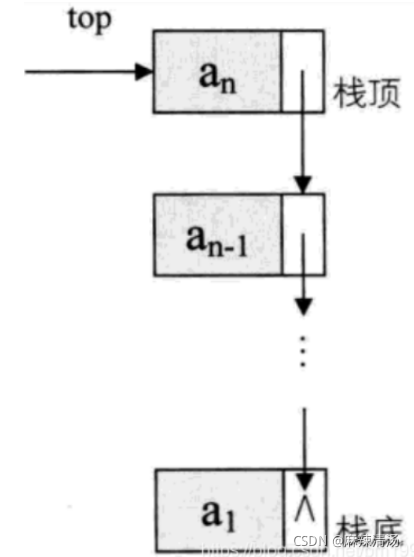
栈的链式存储结构

简称链栈

空栈：top=NULL

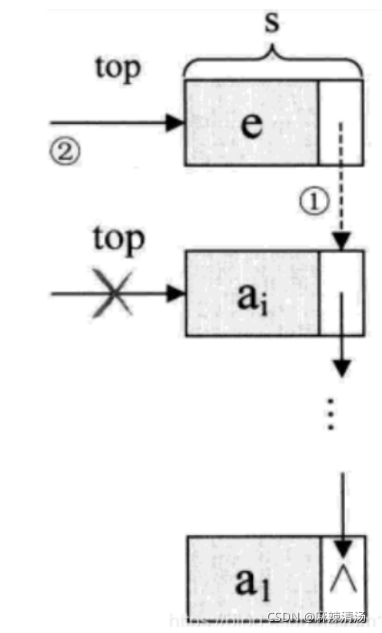
栈的链式存储结构--进栈操作

进栈push操纵，假设元素为e的新结点是s，top为栈顶指针

/*插入元素e为新的栈顶元素*/
Status push(LinkStack *S,SElemType e)
{
    LinkStackPtr s=(linkStackPtr)malloc(sizeof(StackNode));
    s->data=e;
    s->next=S->top;  //后继链接
    S->top=s;         //改变top位置
    S->count++;
    return OK;
}

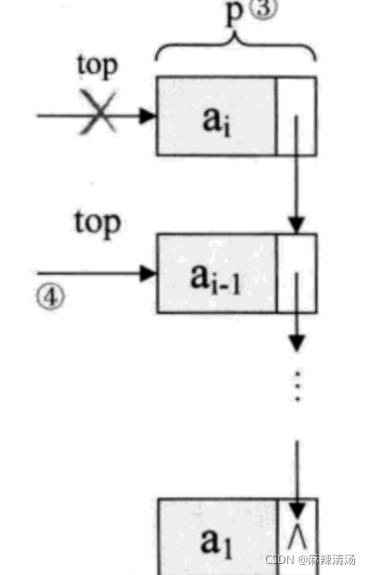
出栈操作

假设变量p用来存储要删除的栈顶结点，将栈顶指针下移一位，最后释放p即可。

/*若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR*/
Status Pop(LinkStack *S,SElemType *e)
{
    LinkStackPtr p;
    if(StackEmpy(S))
    {
        return ERROR;
    }
    *e=S->top->data;
    p=S->top;
    S->top=S->top->next;
    free(p); //释放
    S->count--;
    return OK;
}

链栈的进栈的push和出栈pop操作都很简单，没有任何循环操作，时间复杂度O（1）

20世纪50年代，波兰逻辑学家Jan Lukasiewicz，想到了一种不需要括号的后缀表达法，我们也把它称为逆波兰（Reverse Polish Notation，RPN）表示。这种后缀表示法，是表达式的一种新的显示方式，非常巧妙地解决了程序实现四则运算的难题。

我们先来看看，对于 "9+(3-1)*3+10/2"，如果要用后缀表示法应该是什么样子："9 3 1- 3*+ 10 2/+"，这样的表达式称为后缀表达式，叫后缀的原因在于所有的符号都是在要运算数字的后面出现。

后缀表达式的计算规则：

从左到右遍历表达式的每个数字和符号，遇到是数字进栈，遇到是符号，就将处于栈顶两个数字出栈并进行运算，运算结果进栈。